Условная вероятность. Вероятность произведения событий.

Зависимые и независимые события.

2 события А и В называются независимыми , если вероятность каждого из них не зависит от появления другого или не появления.

В противном случае события называются зависимыми.

Произведение событий.

Определение: Произведением двух событий А и В называется событие АВ=А дуга В состоящее в одновременном появлении как события А так и события В

Пример. Пусть событие А есть выигрыш по займу 1, событие В выигрыш по второму займу. Тогда событие А+В есть выигрыш хотя бы по первому займу, возможно и по второму.

Определение:

Условная вероятность, вероятность события А при условии, что произошло событие В называется условной вероятностью условия А

Р(А/В)=Рв(А); Рв(А)=Р(ВА)/Р(В); Р(В)>0

Пример: 3 белых шара, 3 черных. Из урны дважды вынимают по 1-му шару не кладут обратно. Найти вероятность появления белого шара при втором испытании (событие А), если при первом испытании был извлечен черный шар
(событие В).

Решение: После 1-го испытания в урне осталось 5 шаров. Искомая условная вероятность Рв(А)=3/5.

2-й способ. Вероятность извлечения белого шара=1/2 Р(А)=Р(В)=1/2.

Вероятность произведения событий т.е. при 1-м черный при 2-м белый общее число исходов 6*5=30. Благоприятных исходов 3*3=9, таким образом Р(АВ)=9/3=3/10 Рв(А)=3/10*1/2= 3/5

Вероятность произведения событий.

Теорема 1 Вероятность произведения совмещение 2-х событий А и В равна произведению вероятности одного на условную вероятность другого в предположении, что первое имеет место. Р(АВ)=Р(А)*Ра(В).

Замечание т.к. ВА=АВ то Р(АВ)=Р(ВА)=Р(В)*Рв(А)

Теорема 2 Вероятность совместного появления двух независимых событий А и В = произведению вероятности этих событий Р(АВ)=Р(А)*Р(В)

Пример: Вероятность поражения цели 1-м стрелком (А) =0,9 Вероятность поражения цели 2-м стрелком(В) =0,8. Какова вероятность того, что цель будет поражена хотя бы одним стрелком.

С с чертой – оба промахнулись.

С с чертой= АВ с чертой т.к. Авероятнос с чертой и В с чертой – независимые события

Р(С с чертой)=Р(А с чертой)Р(В с чертой)=(1-Р(А))(1-Р(В))=0,1*0,2=0,02 – вероятность что оба промахнулись. Р(С)=1-Р(С с чертой)=0,98

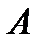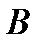Теорема.Вероятность произведения событий и равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:

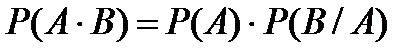или 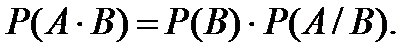(3.14)

Условие независимости события 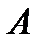от события 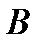можно записать в виде 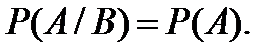Из этого утверждения следует, что для независимых событий выполняется соотношение:

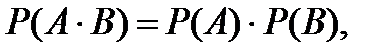(3.15)

т. е. вероятность произведения независимых событи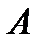й и 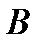, равна произведению их вероятностей.

Замечание.Вероятность произведения нескольких событий 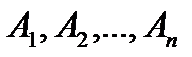равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что все предыдущие имели место:

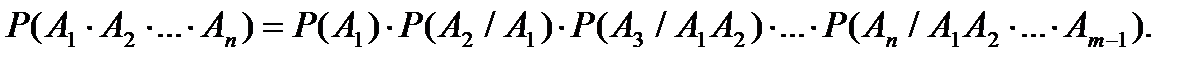
Если события независимые, то имеем:

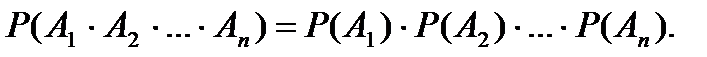
Независимость событий.

Перед тем как изложить теорему умножения вероятностей, введем одно важное понятие: понятие о зависимых и независимых событиях.

Событие A называется независимым от события B, если вероятность события A не зависит от того, произошло событие B или нет.

Событие A называется зависимым от события B, если вероятность события A меняется в зависимости от того, произошло событие B или нет.