Формулы комбинаторики: размещения, сочетания, перестановки.

Формулы комбинаторики

Рассмотрим задачу подсчета числа выборок из данного множества в общем виде. Пусть имеется некоторое множество N, состоящее из n элементов. Любое подмножество, состоящее из m элементов можно рассматривать без учета их порядка, так и с его учетом, т.е. при изменении порядка переходим к другой m – выборке.

Сформулируем следующие определения:

Размещения без повторения

Размещением без повторения из n элементов по m называется всякое упорядоченное подмножество множества N, содержащее m различных элементов.

Из определения следует, что два размещения отличаются друг от друга, как элементами, так и их порядком, даже если элементы одинаковы.

Теорема 3. Число размещений без повторения равно произведению m сомножителей, наибольшим из которых является число n. Записывают:

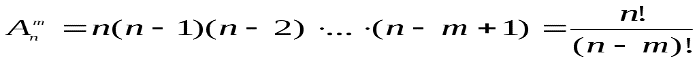
Перестановки без повторений

Перестановками из n элементов называются различные упорядочения множества N.

Из этого определения следует, что две перестановки отличаются только порядком элементов и их можно рассматривать как частный случай размещений.

Теорема 4. Число различных перестановок без повторений вычисляется по формуле

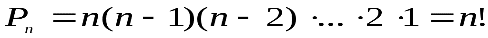
Сочетания без повторений

Сочетанием без повторения из n элементов по m называется любое неупорядоченное подмножество множества N, содержащее m различных элементов.

Из определения следует, что два сочетания различаются только элементами, порядок не важен.

Теорема 5. Число сочетаний без повторений вычисляют по одной из следующих формул:

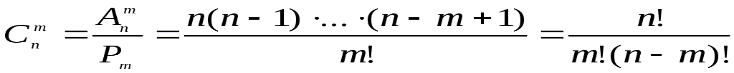
Пример 1. В комнате 5 стульев. Сколькими способами можно разместить на них

а) 7 человек; б) 5 человек; в) 3 человека?

Решение: а) Прежде всего надо выбрать 5 человек из 7 для посадки на стулья. Это можно сделать 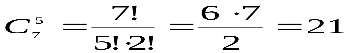способом. С каждым выбором конкретной пятерки можно произвести 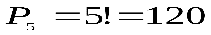перестановок местами. Согласно теореме умножения искомое число способов посадки равно .

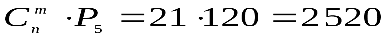Замечание: Задачу можно решать, используя только теорему произведения, рассуждая следующим образом: для посадки на 1-й стул имеется 7 вариантов, на 2-й стул-6 вариантов, на 3-й -5, на 4-й -4 и на 5-й -3. Тогда число способов посадки 7 человек на 5 стульев равно 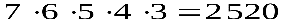. Решения обоими способами согласуются, так как

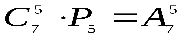
б) Решение очевидно -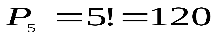

в) 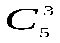- число выборов занимаемых стульев.

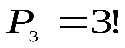- число размещений трех человек на трех выбранных стульях.

Общее число выборов равно .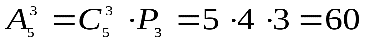

Не трудно проверить формулы ;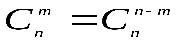

;

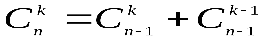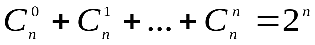- число всех подмножеств множества, состоящего из n элементов.

Вероятность суммы событий.

Пусть А и В – два несовместных события. Тогда в соответствии с третьей аксиомой для вероятности имеем

P(A+B) = P(A) + P(B). (3.6)

Это равенство известно как теорема сложения вероятностей несовместных событий. Для классической схемы это свойство не нужно постулировать, т.к. легко выводится из классического определения вероятности (доказать самостоятельно).

Пример 3.5. Из колоды в 36 карт наугад вынимают 3 карты. Найти вероятность того, что среди них окажется хотя бы один туз.

Решение. Введем следующие события: B={появление хотя одного туза}, A₁={появление одного туза}, A₂={появление двух тузов}, A₃={появление трех тузов}. Очевидно, что B=A₁+A₂+A₃. Поскольку события A₁, A₂ и A₃.несовместны, то

P(B) = P(A₁)+P(A₂)+P(A₃) =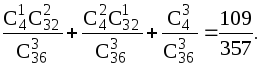

Эту задачу можно решить иначе. Событие 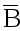, противоположное событию В, состоит в том, что среди вынутых из колоды трех карт нет ни одного туза. ПосколькуP(B)+P( 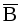)=1, то

P(B) = 1 – P( ) =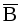

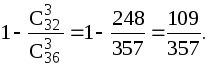
Пусть А и В – два произвольных события, т.е. они, в общем случае, совместны. Запишем события А+В и В в виде

A+B = A+B 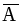и B = B 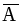+BA.

(объясните эти равенства, используя диаграммы Вьенна). Поскольку событие, стоящие в правых частях этих равенств, несовместны, то

P(A+B) = P(A) + P(B 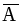), P(B) = P(B 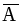)+P(BA).

Исключая P(B 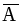),получим

P(A+B) = P(A)+P(B)–P(AB). (3.7)

Это равенство известно как теорема сложения вероятностей совместных событий.

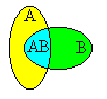
Полученная формула сложения вероятностей хорошо иллюстрируется при помощи диаграмм Вьенна. Здесь следует помнить, что вероятность события пропорциональна площади фигуры, которая соответствует данному событию. Событию А+В на рисунке соответствует вся заштрихованная фигура, площадь которой можно представить в виде суммы трех слагаемых S_A+B=S₁+S₂+S_AB, где S₁ соответствует событию А–АВ, а S₂ – событию В–АВ. Тогда, событию А будет соответствовать фигура с площадью S_А= S₁+S_АВ, а событию В – S_В= S₂+S_АВ. В результате получим, что S_А+В= S_А+S_В–S_АВ. Полученное равенство соответствует теореме сложения вероятностей.

Теорему сложения вероятностей можно обобщить на случай произвольного числа слагаемых. Вчастности,

P(A+B+C) = P(A)+P(B)+P(C)–(AB)–P(AC)–P(BC)+P(ABC). (3.8)

Докажите данную формулу самостоятельно.

Пример 3.6. Два стрелка делают по одному выстрелу по мишени. Вероятность попадания для первого стрелка равна 0,8, для второго – 0,7. Какова вероятность поражения цели?

Решение. Пусть A₁={первый стрелок попал по цели}, A₂={второй стрелок попал по цели}. Мишень будет поражена (событие В), если произойдет событие А₁+А₂. Поскольку события А₁ и А₂ совместны, но независимы, то

P(А₁+А₂) = P(А₁)+P(А₂)–P(А₁)P(А₂) = 0,7+0,8–0,7×0,8 = 0,94.

Отметим, что событие В можно записать также в виде A₁ 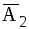+ 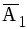A₂+A₁A₂. Тогдаполучим

P(B) = P(A₁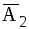)P( )+P( 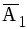)P(A₂)+P(A₁)P(A₂) = = 0,8×0,3+0,2×0,7+0,7×0,8 = 0,94.

Однако такой путь слишком длинный.