Тема 2. ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ

НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ

Задача 21–40.Даны координаты вершин треугольника АВС.

Найти:

1) длину стороны АВ;

2) уравнения сторон АВ и ВС и их угловые коэффициенты;

3) угол В (в радианах с точностью до двух знаков);

4) уравнение высоты СD и ее длину;

5) уравнение медианы АЕ и координаты точки К пересечения этой медианы с высотой СD;

6) уравнение прямой, проходящей через точку К, параллельно стороне АВ.

21. А(-7;4); В(5;-5); С(3;9).	22. А(0;3); В(12;-6); С(10;8).
23.А(-5;9); В(7;0); С(5;14).	24.А(4;1); В(16;-8); С(14;6).
25.А(-3;10); В(9;1); С(7;15).	26.А(-4;12); В(8;3); С(6;17).
27.А(-6;8); В(6;-1); С(4;13).	28.А(3;6); В(15;-3); С(13;11).
29.А(-10;5); В(2;-4); С(0;10).	30.А(-2;7); В(10;-2); С(8;12).
31.А(-1;4); В(11;-5); С(15;17).	32.А(2;5); В(14;-4); С(18;18).
33.А(-4;10); В(8;1); С(12;23).	34.А(1;0); В(13;-9); С(17;13).
35.А(-9;6); В(3;-3); С(7;19).	36.А(0;2); В(12;-7); С(16;15).
37.А(- 8;-3); В (4;-12);С(8;10).	38.А(-5; 7);В (7; -2); С(11; 20).
39.А(-12;-1);В(0;-10); С(4;12).	40.А (-10; 9); В (2; 0);С (6; 22).

Решение типового примера

А(0; 1), В(6; 4), С(3; 5) – координаты вершин треугольника АВС.

1. Длину стороны АВ найдем как расстояние между точками ;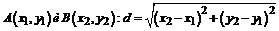

.

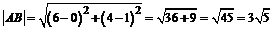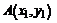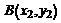2. Уравнение прямой, проходящей через точки и , найдем по формуле ;

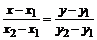АВ: 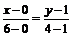; ; 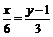; ; 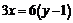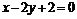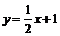–уравнение АВ. .

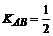ВС: 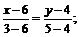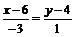; ; 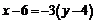; ; 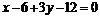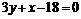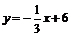– уравнение ВС . .

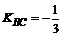3.Тангенс угла α между двумя прямыми, угловые коэффициенты которых соответственно равны K₁ и K₂, вычисляется по формуле .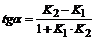

Искомый угол В образован прямыми АВ и АС: ; ;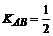

,

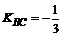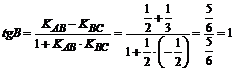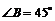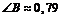, или рад.

4. Высота 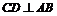, следовательно ее угловой коэффициент найдем из условия перпендикулярности двух прямых:

.

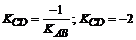Тогда уравнение СD будет иметь следующий вид:

; .

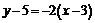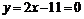Длину высоты СD найдем как расстояние от точки С до прямой АВ, используя формулу расстояния от точки 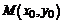до прямой 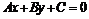; 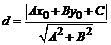. Уравнение АВ: 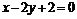; С(3;5); тогда .

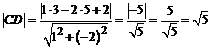5. Точка Е является серединой отрезка ВС:

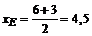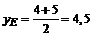; . E(4,5;4,5).

AE: ;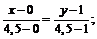

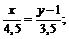
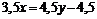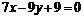– уравнение АЕ.

Для того, чтобы найти точку K пересечения медианы АЕ и высоты СД решим систему уравнений: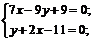

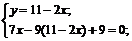
x=3,6 y=3,8. Точка K(3,6;3,8).

6.Прямая, параллельная АВ, будет иметь угловой коэффициент, равный угловому коэффициенту АВ: 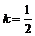. Тогда уравнение прямой, проходящей через точку К параллельно АВ, будет иметь такой вид:

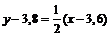или .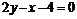

Задачи 41–60. Даны координаты точек А, ВиС.

Требу­ется:

1) составить канонические уравнения прямой АВ;

2) соста­витьуравнение плоскости Р, проходящей через точку С перпендикулярно прямой АВ;

3) найтиточку пересечения этой плоскости с пря­мой АВ;

4) найти расстояние от точки В до плоскости Р.

61. А(3;-1; 5);	В(7; 1; 1);	С(4;-2; 1).
62. А(-1; 2; 3);	В(3; 4; -1);	С(0; 1; -1).
63. А (2; -3; 7);	В(6; -1; 3);	С(3; -4; 3).
64. А(0; -2; 6);	В(4; 0; 2);	С(1;-3; 2).
65. А(-3; 1; 2);	В(1; 3; -2);	С(-2; 0; -2).
66. А(-2; 3; 1);	В(2; 5; -3);	С(-1; 2; -3).
67. А(-4; 0; 8);	В(0; 2; 4);	С(-3; -1; 4).
68. А(1- 4; 0);	В(5; 6; -4);	С(2; 3; -4)
69. А(4; -4; 9);	В(8;-2; 5);	С(5; -5; 5).
70. А(5; 5; 4);	В(9; 7; 0);	С(6; 4; 0).
71. А(-3; -2; -4);	В(-4; 2; -7);	С(5; 0; 3).
72. А(2; -2; 1);	В (-3; 0; -5);	С(0; -2; -1).
73. А (5; 4; 1);	В(-1; -2; -2);	С(3; -2; 2).
74. А(3; 6; -2);	В(0; 2; -3);	С(1; -2; 0).
75. А(1; -4; 1);	В(4; 4; 0);	С(-1; 2; -4).
76. А (4; 6; -1);	В(7; 2; 4);	С(-2; 0; -4).
77. А(0; 6; -5);	В(8; 2; 5);	С(2; 6; —3).
78. А(-2; 4; -6);	В(0; -6; 1);	С (4; 2; 1).
79. А(-4;-2;-5);	В(1; 8;-5);	С (0; 4;- 4).
80. А(3; 4;-1);	В(2;-4; 2);	С(5; 6; 0).

Решение типового примера

Пусть А(4;-1;-3), В(2;-3;-2), С(-3;2;3).

1. Канонические уравнения прямой в пространстве имеют следующий вид:

,

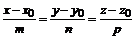где х , у , z– координаты точки, через которую проходит прямая;

m, n, p–координаты направляющего вектора этой прямой; в данном случае это будут координаты вектора 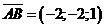. Тогда уравнения прямой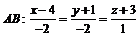

2. Уравнение плоскости, проходящей через данную точку М(х,y,z), перпендикулярно данному вектору 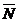(A,B,C):

А(х-х₀ )+В(у-у₀ )+С(z-z₀ )=0.

Тогда уравнение плоскости Р: -2(х+3)-2(у-2)+(z-3)=0.

После упрощения: -2х-2у+z -5=0 или 2х+2у-z +5=0.

3. Для того, чтобы найти точку пересечения прямой и плоскости,

нужно уравнения прямой представить в параметрическом виде:

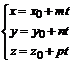, где t –параметр.

Уравнение АВ в параметрическом виде: .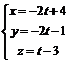

Подставим эти значения в уравнение плоскости Р: , ,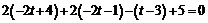

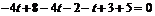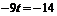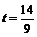, . Тогда 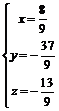, т.е. точка пересечения М прямой АВ и плоскости Р имеет координаты: .

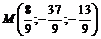4. Расстояние от точки 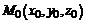до плоскости 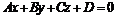вычисляем по формуле: .

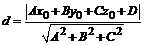Найдем расстояние от точки А до плоскости Р: .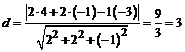

Тема 3. ВВЕДЕНИЕ В МАтематический анализ

Функции одной переменной

Для успешного усвоения этой темы необходимо разобраться в фундаментальном понятии математического анализа – понятии функции, изучить способы задания функции, свойства основных элементарных функций. При исследовании и анализе поведения функций не обойтись без понятий предела функции, бесконечно малой величины, ограниченной и непрерывной функций. Теоремы о пределах, замечательные пределы играют особую роль при решении задач по этой теме.

ВОПРОСЫ ДЛЯ ИЗУЧЕНИЯ И САМОПРОВЕРКИ

1. Множество действительных чисел. Функция, бластьопределения функции, способы задания функции.

2. Основные элементарные функции, их свойства и графики.

3. Сложные и обратные функции, их графики.

4. Предел функции в точке и на бесконечности. Теоремы о преде-лах. Замечательные пределы.

5. Пределы монотонных функций.

6. Непрерывность функций в точке, на интервале.

7. Непрерывность основных элементарных функций.

8. Бесконечно малые и бесконечно большие функции, их свойства. Сравнение бесконечно малых.

9. Свойства непрерывных на отрезке функций.

Задачи 61–80.Найти пределы заданных функций.

61. а) 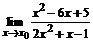,	при , , ;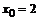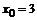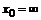
б) 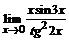;	в) .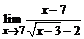
62. а) 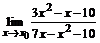,	при , , ;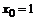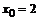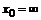
б) 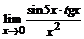;	в) .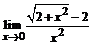
63. а) 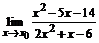,	при , , ;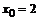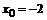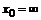
б) 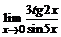;	в) .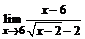
64. а) 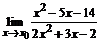,	при , , ;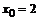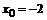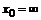
б) 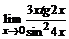;	в) .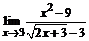
65. а) 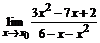,	при , , ;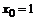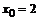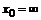
б) 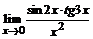;	в) .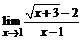
66. а) 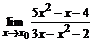,	при , , ;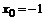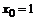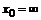
б) 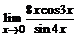;	в) .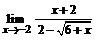
67. а) 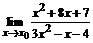,	при , , ;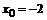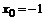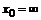
б) 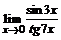;	в) .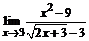
68. а) 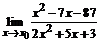,	при , , ;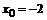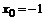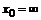
б) 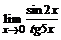;	в) .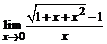
69. а) 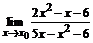,	при , , ;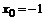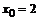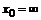
б) 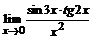;	в) .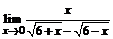
70. а) 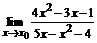,	при , , ;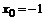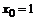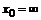
б) 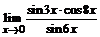;	в) .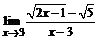
71. а) 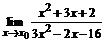,	при , , ;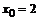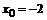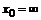
б) 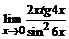;	в) .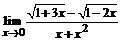
72. а) 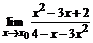,	при , , ;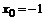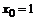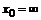
б) 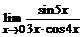;	в) .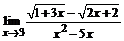
73. а) 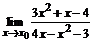,	при , , ;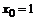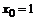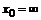
б) 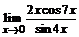;	в) .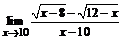
74. а) 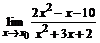,	при , , ;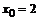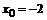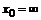
б) 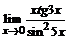;	в) .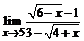
75. а) 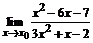,	при , , ;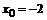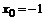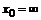
б) 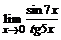;	в) .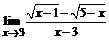
76. а) 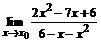,	при , , ;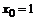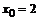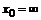
б) 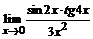;	в) .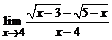
77. а) 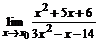,	при , , ;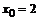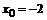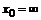
б) 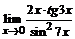;	в) .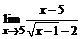
78. a) 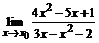,	при , , ;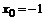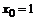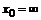
б) 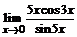;	в) .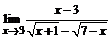
79. a) 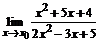,	при , , ;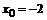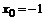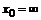
б) 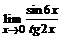;	в) .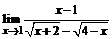
80. а) 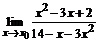,	при , , ;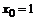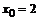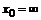
б) 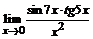;	в) .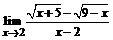

Решение типовых примеров

П р и м е р ы. Найти указанные пределы:

1. .

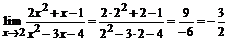2. .

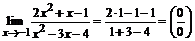При подстановке предельного значения х=-1 получим неопределенность вида 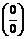. Для раскрытия неопределенности в данном случае разложим числитель и знаменатель дроби на линейные множители по формуле: 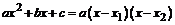, где х₁ и х₂ –корни квадратного трехчлена .

.

.

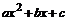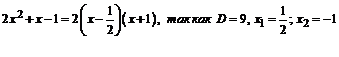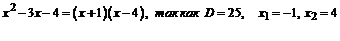Следовательно: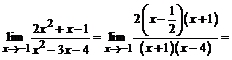

.

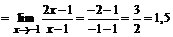3. 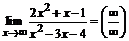Для раскрытия неопределенности

разделим числитель и знаменатель дроби на переменную в старшей степени, т.е. на х²:

.

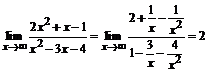4. 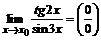. В данном случае неопределенность вида 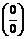раскрываем с использованием первого замечательного предела и его следствия: ; .

.

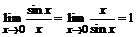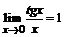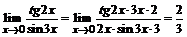5. 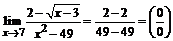. Для раскрытия данного вида неопределенности нужно домножить числитель и знаменатель дроби на выражение, сопряженное числителю:

=

.

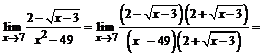
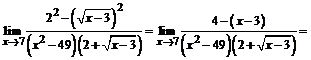
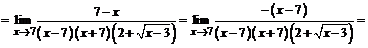
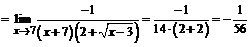Необходимо знать формулу: 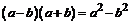.