Удар при кручении. Защита приборов

И оборудования от ударов. Определение напряжений

При ударном воздействии

Определим динамический крутящий момент и динамическое напряжение, возникающее в сечении вала при ударе, вызванном внезапной остановкой его левого конца А.

Пусть вал с диском (массой), момент инерции которого относительно продольной оси вращения равен J_m>0, вращается с угловой скоростью . Если внезапно остановить левый конец стержня, то вся кинетическая энергия, которой обладает диск, обратится в потенциальную энергию деформации вала (рис. 13.15).

Рис. 13.15. Схема крутильного удара

Энергия диска вызывает динамический крутящий момент. Кинетическая энергия диска

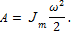
Потенциальная энергия, накопленная в брусе,

где М_дин – действующий крутящий момент, эквивалентный по результатам своего действия явлению крутящего удара;

– динамический угол закручивания вала.

Согласно закону сохранения энергии имеем:

·

Учитывая, что

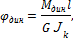
получим

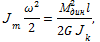
тогда

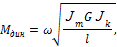
где ω – угловая скорость вращения системы;

GJ_к – жесткость сечения вала при кручении;

J_m – момент инерции массы диска относительно оси вращения;

l – длина части бруса, подвергающейся деформации.

Зная M_дин, находим максимальное напряжение при крутящем yдаре, как при статическом кручении:

для круглого сечения:

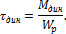
Динамический угол закручивания:

Условие прочности при динамическом нагружении:

где [ ] – допускаемая величина нормальных напряжении при ударе.

Для пластичного материала

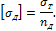
Величину коэффициента запаса можно было бы выбрать равной величине основного коэффициента запасаn при статическом действии нагрузок (1,4–1,6), так как динамичность уже учтена динамическим коэффициентом. Однако, учитывая, что рассмотрен приближенный метод расчета на удар, этот коэффициент принимают несколько завышенным (до 2). Кроме того, обычно в этих случаях применяют материал более высокого качества в отношении однородности и пластических свойств.

Пример расчета

Задача 1.Шахтная подъемная машина поднимает равноускоренно груз G = 50 кН. За первые 3 с груз поднимается на высоту h = 18 м. Длина каната l = 200 м. Удельный вес материала каната γ = 78 ×10³ Н/м, допускаемое напряжение 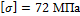. Определить площадь поперечного сечения каната с учетом и без учета его собственного веса.

Решение.

1. Определим ускорение, с которым поднимается груз G:

2. Определим площадь поперечного сечения каната без учета его собственного веса по формуле

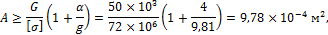
3. Определим площадь поперечного сечения каната с учетом его собственного веса из условия прочности по формуле

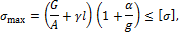
откуда

.

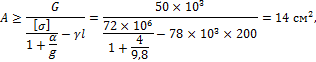
Задача 2. Вал AB диаметром d = 50 мм равномерно вращается вокруг своей оси с угловой скоростью . На рычаге СД с валом жестко соединен груз G = 200 H (рис. 13.16, а). Проверить прочность вала, если . Собственным весом системы пренебречь.

Решение.

1. Составляем расчетную схему (рис. 13.16, б). Определим усилие, действующее на вал от груза G при его вращении:

2. Методом сечений строим эпюру изгибающих моментов (рис. 13.16, в).

3. Проверяем прочность вала:

М_max= 1915 Hм;

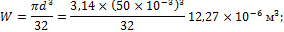
σ_max = 156 Мпа < [σ] = 160 МПа.

Прочность вала обеспечена.

Рис. 13.16. Схема вала с грузом на рычаге

Задача 3. Стальная проволока ОА длиной l = 0,8 м и диаметром d = 2 мм равномерно вращается вокруг точки О (рис. 13.17). На конце проволоки подвешен груз G = 20 H. При какой угловой скорости произойдет разрушение проволоки, если σ_в = 800 МПа?

Рис. 13.17. Схема вращающегося груза

на проволоке

Решение.

1. Определяем площадь поперечного сечения проволоки:

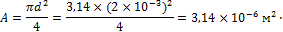
2. Усилие, возникающее в проволоке при вращении груза вокруг точки О, определяется по формуле

3. Определим напряжение, возникающее в проволоке:

тогда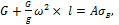

откуда

Задача 4. Определить максимальное нормальное напряжение в стальном шатуне АВ прямоугольного поперечного сечения b ´ h = 20 ´50 мм (рис. 13.18). Кривошип СА вращается с угловой скоростью 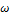= 30 c^–1. Удельный вес материала шатуна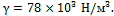

Решение.

1. Составляем расчетную схему (рис. 13.18, б).

2. Определим площадь поперечного сечения шатуна:

A = b ´ h = (20 50) ´ 10^–6 = 1 ´ 10^–3 м².

3. Определим нормальное ускорение точки А шатуна:

4. Определим нормальное ускорение точки B шатуна:

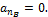
5. Находим максимальную интенсивность сил инерции шатуна:

6. Строим эпюру изгибающих моментов (рис. 13.18, в).

Рис. 13.18. Схема кривошипно-шатунного механизма

7. Вычисляем максимальные нормальные напряжения:

.

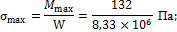
Задача 5. Стальные стержни Ӏ и ӀӀ испытывают удар одинаковым грузом G = 10 Н, падающим с одинаковой высоты h = 0,1 м (рис. 13.19). Определить и сравнить возникающие в стержнях динамические напряжения. Массой стержня пренебречь. E = 2 ´ 10⁵ МПа.

Рис. 13.19. Схема стержней, испытывающих удар

Решение.

I вариант.

1. Определим cтатическое напряжение, действующее в поперечном сечении стержня (рис. 13.19, а):

2. Определим абсолютную деформацию стержня при статической нагрузке:

3. Определим динамический коэффициент:

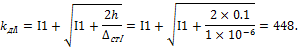
4. Определим динамическое напряжение в поперечном сечении стержня:

II вариант.

5. Определим статическое напряжение:

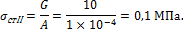
6. Определим абсолютную деформацию ступенчатого стержня при статической нагрузке:

.

7. Определим динамический коэффициент:

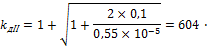
8. Определим динамическое напряжение в поперечном сечении ступенчатого стержня:

на

Задача 6.Стальной стержень диметром d = 25 мм и длиной l = 1,5 м растянут внезапно приложенной силой F = 25 кH. Определить напряжение и удлинение стержня.

Решение.

1. При внезапном приложении нагрузки к стальному стержню

2. Определяем динамические напряжения:

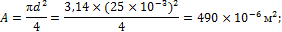
3. Определяем удлинение стержня:

Задача 7. Проверить прочность деревянной консольной балки прямоугольного поперечного сечения b ´ h = 60 ´ 100 мм, на конец консоли которой падает груз G = 10 H (рис. 13.20). Скорость груза к моменту соударения ν = 2 м/с;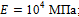

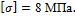
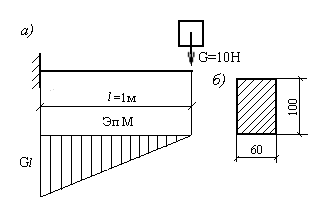
Рис. 13.20. Схема деревянной консольной балки

Решение.

1. Определим геометрические характеристики поперечного сечения:

2. Определим статический прогиб на консоли балки:

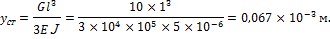
3. Определим динамический коэффициент:

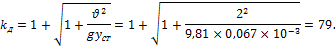
4. Определим максимальные статические напряжения:

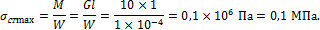
5. Определим максимальные динамические напряжения:

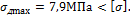
Условие прочности соблюдается.

Задача 8.Маховик диаметром D = 0,2 м и весом G = 0,5 кH, насаженный на вал AB длиной l = 1 м и диаметром d = 60 мм (рис. 13.21), вращается с угловой скоростью . Определить величину наибольших касательных напряжений в тот момент, когда конец вала внезапно останавливается (крутящий удар). Массой вала пренебречь; .

Решение.

1. Определим изменение кинетической энергии в момент удара:

или

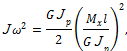
откуда

Рис. 13.21. Схема вала с маховиком

2. Определим момент инерции массы маховика:

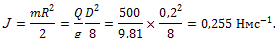
3. Полярный момент инерции:

4. Полярный момент сопротивления:

5. Определим крутящий момент на валу:

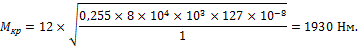
6. Определим касательные напряжения в поперечном сечении вала:

13.5. Задачи для самостоятельного решения

Задача 9.Чугунный обод маховика диаметром D = 0,5 м и площадью поперечного сечения A = 40 см² вращается с постоянной угловой скоростью 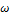= 100 c^–1 (рис. 13.22). Допускаемое напряжение на растяжение [σ]_р = 7 Мпа. Удельный вес чугуна γ = 78 × 10^–3 Н/м³. Проверить прочность обода.

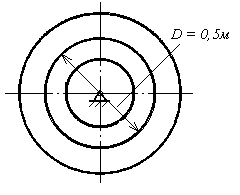
Рис. 13.22. Схема маховика

с чугунным ободом

Ответ: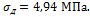

Задача 10.Груз весом G = 5 кH падает с высоты h = 20 мм на двутавровую балку № 20 длиной l = 4 м шарнирно опертыми концами (рис. 13.23).

Проверить прочность и определить максимальный прогиб балки при ударе 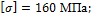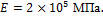Массой балки пренебречь.

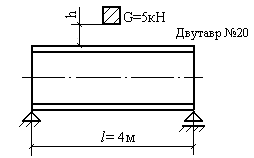
Рис. 13.23. Схема двутавровой балки

Ответ:

Задача 11.Решить задачу 10 при условии, что один конец балки шарнирно оперт, а второй опирается на пружину (рис. 13.24), жесткость которой

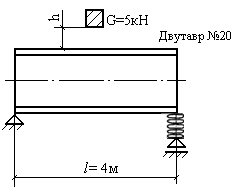
Рис. 13.24. Схема двутавровой балки,

опирающейся одним концом на пружину

Ответ: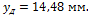

13.6. Контрольные вопросы

1. Какие виды динамических нагрузок существуют?

2. Что такое силы инерции? Как они учитываются в динамических расчетах? Определение динамического коэффициента.

3. Какие существуют критерии определения критической скорости вращения вала?

4. Что такое ударная динамическая нагрузка?

5. В чем существует различие между продольным и поперечным ударом?

6. Как определяется динамический коэффициент при ударе?

7. Как определяется динамический коэффициент при ударе стержней с переменным поперечным сечением?

8. Как влияет учет массы ударяемого стержня на величину динамического коэффициента?

9. Что такое крутильный удар?

10. Как определяется динамический угол закручивания?

11. Как определяются допустимые напряжения при ударе?

12. Как выполняется расчет на прочность при ударе?

ПРИЛОЖЕНИЯ

Приложение 1