Статически неопределимые задачи на кручение

Рассмотрим расчет статически неопределимой системы на кручение на конкретном примере.

Пример. Определить из расчета на прочность при 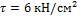допускаемое значение скручивающего момента для вала, жестко защемленного обоими концами и нагруженного, как показано на рис. 10.8, а.

Рис. 10.8. Схема статически неопределимого вала

В заделках возникают реактивные моменты m_A и m_B (рис. 10.8, а). Составим уравнение равновесия относительно продольной оси вала:

Таким образом, задача является один раз статически неопределимой – одно уравнение статики и два неизвестных реактивных момента. Для составления уравнения перемещений отбросим правую заделку, заменив ее действие на вал неизвестным реактивным моментом . Полученная таким образом статически определимая система (рис. 10.8, б) эквивалентна заданной, и, следовательно, угол поворота сечения B равен нулю:

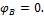
Применяя принцип независимости действия сил, запишем уравнение перемещений для сечения B в виде

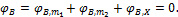
При действии только момента m₁ угол поворота сечения В равен углу закручивания участка АС, т. е.

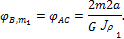
Аналогично при действии только момента m₂:

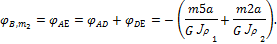
При действии только момента m_B = X имеем:

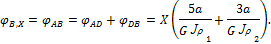
Для упрощения вычислений выразим

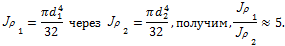
Подставляя значения углов поворота в уравнение совместности деформаций и учитывая последнее равенство, получаем:

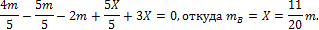
Подставляя значение Х в уравнение равновесия, найдем:

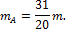
После раскрытия статической неопределимости эпюры крутящих моментов, касательных напряжений и углов закручивания строятся обычным способом. Эта эпюры представлена на рис. 10.8, в, г, д.

Опасными являются сечения участка ВЕ. Следует отметить, что сечения, в которых возникают наибольшие крутящие моменты (участок АС), в данном случае менее опасны.

Запишем условие прочности:

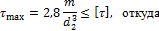
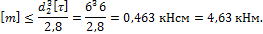
Расчет цилиндрических винтовых пружин

С малым шагом витков

Во многих механизмах и машинах, например в рессорах вагонов и автомобилей, применяют винтовые пружины. Эти пружины навивают из проволоки круглого поперечного сечения, изготовленной из специальных марок стали. При проектировании таких пружин необходимо уметь вычислять наибольшие напряжения (для проверки на прочность) и определять деформацию пружины (ее удлинение или прогиб). Точный расчет винтовых пружин достаточно сложен, так как материал пружины испытывает одновременно кручение, сдвиг, изгиб и растяжение.

Пружина с малым шагом витков – это такая пружина, у которой угол между плоскостью, перпендикулярной к оси пружины, и плоскостью витка не превышает 14º.

Пусть винтовая пружина растягивается (или сжимается) силами F, имеет средний диаметр D = 2R и изготовлена из проволоки диаметром d (рис. 10.9, а). Для определения внутренних усилий в пружине применим метод сечений.

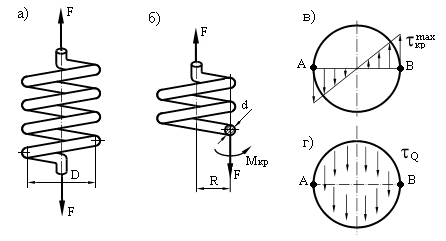
Рис. 10.9. Схема винтовой пружины с малым шагом витков

Верхняя часть пружины (рис. 10.9, б) будет находиться в равновесии под действием внешней силы F и внутренних усилий в проведенном сечении прутка, которые можно представить суммой силы F и крутящего момента М_кр.

Считая, что угол наклона витка 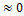, можно пренебречь остальными силовыми факторами (продольной силой и изгибающим моментом). Материал пружины испытывает срез и кручение.

Сила 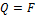вызывает в поперечном сечении касательные напряжения 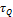, которые определяются по формуле

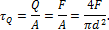
Считаем, что касательные напряжения 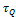распределяются по сечению равномерно (рис. 10.9, г).

Максимальные касательные напряжения от кручения равны:

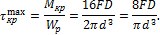
Распределение касательных напряжений от кручения показано на рис. 10.9, в.

Опасной точкой на контуре сечения является точка А, в которой направления касательных напряжений совпадают. Таким образом, максимальные касательные напряжения равны:

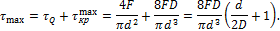
Так как 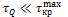и на практике 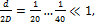то часто действием 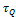пренебрегают.

Условие прочности для пружин малой кривизны (приближенный расчет):

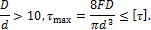
Условие прочности для пружин малой кривизны:

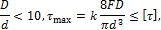
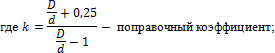
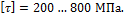
Из формул для определения 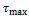следует, что увеличение диаметра пружины D уменьшает ее прочность, а увеличение диаметра проволоки d – увеличивает.

При определении деформации пружины будем учитывать только кручение витков.

Изменение длины пружины вдоль оси под действием внешней нагрузки называется осадкой пружины λ, которая определяется по формуле

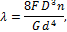
где n – число витков;

G – модуль сдвига.

Зависимость осадки λ от осевой нагрузки F называется характеристикой пружины. Обычные пружины имеют линейную характеристику.

Усилие F, при котором перемещение λ равно единице (1 м), называется жесткостью пружины с, которая определяется по формуле

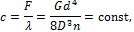
размерность жесткости кН/м.

Итак, увеличение числа витков n и диаметра пружины D уменьшает жесткость пружины, а увеличение диаметра проволоки d повышает жесткость пружины.

Пример расчета

Задача 1.Для заданной схемы (рис. 10.10, а) определить значение m и построить эпюру крутящих моментов.

Решение.

1. Методом сечений на каждом участке вала определяем значение крутящего момента.

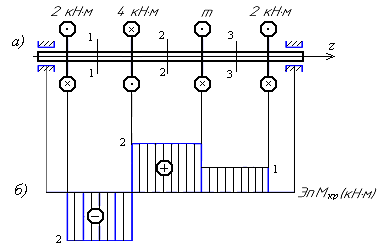
Рис. 10.10. Схема вала для построения эпюры

крутящих моментов

1-й участок. Рассмотрим равновесие левой отсеченной части вала. Составим уравнение равновесия:

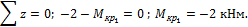
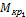на 1-м участке имеет отрицательное значение, так как со стороны внешней нормали к отсеченной части вращается по часовой стрелке.

2-й участок:

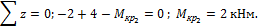
3-й участок:

с другой стороны:

2. Эпюра с учетом знаков построена на рис. 10.10, б.

Задача 2. Вал круглого поперечного сечения диаметром d = 40 мм скручивается моментами m₁ = 0,6 кНм, m₂ = 1,2 кНм и m₃ = 0,8 кНм (рис. 10.11, а). Проверить прочность вала и определить абсолютный угол закручивания концевого сечения, если [τ] = 80 МПа, G = = 8×10⁴ МПа.

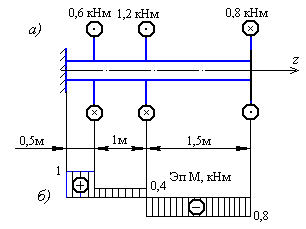
Рис. 10.11. Схема вала круглого поперечного сечения

Решение.

1. Методом сечений строим эпюру крутящих моментов (рис. 10.11, б).

2. Определим геометрические характеристики поперечного сечения вала:

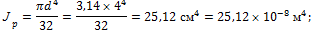
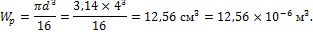
3. Проверяем прочность вала:

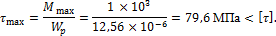
4. Определяем абсолютный угол закручивания концевого сечения:

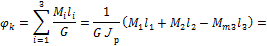
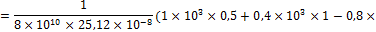
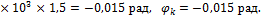
Задача 3. Построить эпюру углов закручивания для ступенчатого стального вала, нагруженного, как показано на рис. 10.12, а. G = = 8×10⁴ МПа.

Решение.

1. Определим геометрические характеристики сечений каждой ступени вала:

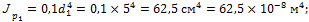
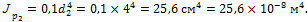
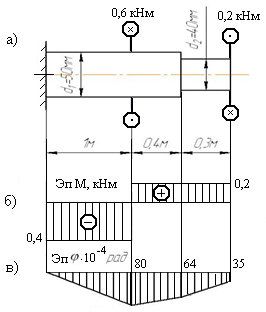
Рис. 10.12. Схема ступенчатого вала

2. Построим эпюру крутящих моментов (рис. 10.12, б).

3. Определим углы закручивания в характерных сечениях вала по формуле

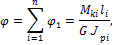
тогда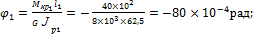

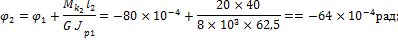
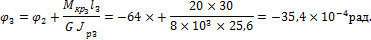
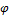изображена на рис. 10.12, в.

Задача 4. Определить внутренний и наружный диаметры полого стального вала, передающего мощность N = 100 кВт и вращающегося с угловой скоростью ω = 80 рад/с, если [τ] = 60 МПа; α = d/D = 0,6, [θ] = 45×10^–4 рад/м, G = 8×10⁴ МПа.

Решение.

1. Определим крутящий момент на валу:

2. Из условия прочности определим момент сопротивления сечения вала:

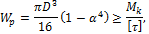
откуда ;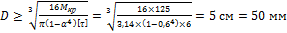

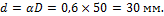
3. Определим наружный диаметр вала из условия жесткости:

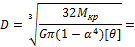
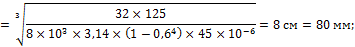
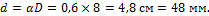
4. Принимаем D = 80 мм, d = 48 мм.

Задача 5. Вал диаметром 90 мм передает мощность N = 80 кВт. Определить предельное число оборотов вала, если [τ] = 60 МПа.

Решение.

1. Определим момент сопротивления поперечного сечения вала:

.

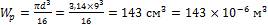2. Из условия прочности определим крутящий момент на валу:

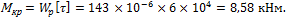
3. Определим предельное число оборотов вала:

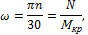
откуда

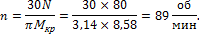
Задача 6. Какую мощность может передать вал, вращающийся с угловой мощностью ω = 20 рад/с, диаметром d = 100 мм при допускаемом напряжении [τ] = 60 МПа и допускаемом угле закручивания
[θ] = 45 × 10^–4 рад/м. Модуль сдвига G = 8 × 10⁴ МПа.

Решение.

1. Определим геометрические характеристики поперечного сечения вала:

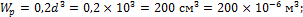
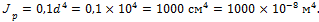
2. Передаваемая валом мощность определяется по формуле

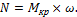
3. Из условия прочности имеем:

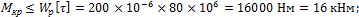
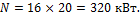
Из условия жесткости:

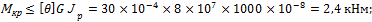
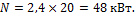
Принимаем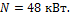

Задача 7. Цилиндрическая пружина, изготовленная из стальной проволоки диаметром d = 6 мм, имеет n = 10 витков. Диаметр пружины D = 66 мм. Пружина растягивается осевыми силами F = 300 Н. Проверить прочность пружины, если [τ] = 240 МПа. Определить удлинение и жесткость пружины и накапливаемую потенциальную энергию.
G = 8 × 10⁴ МПа.

Решение.

1. Определим поправочный коэффициент:

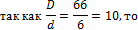
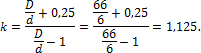
2. Определим касательные напряжения, возникающие в поперечных сечениях прутка пружины:

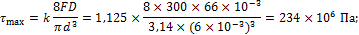
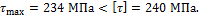
3. Определим удлинение пружины под действием внешней нагрузки:

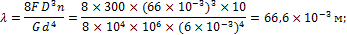
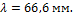
4. Определим жесткость пружины:

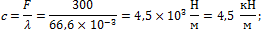
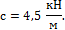
5. Определим потенциальную энергию деформации:

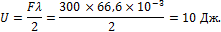
Задача 8.Стальная цилиндрическая пружина сжимается осевыми силами F (рис. 10.13). Пружина навита из проволоки диаметром d = 5 мм, с шагом t = 10 мм и имеет диаметр D = 30 мм. Определить значение сил F, при которых будет достигнута ее предельная осадка. G = 8 × 10⁴ МПа.

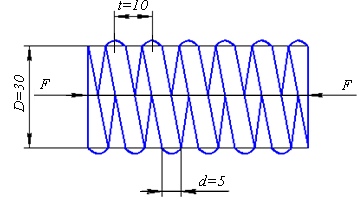
Рис. 10.13. Схема пружины, сжатой осевыми силами

Решение.

1. Запишем условие жесткости пружины при сжатии:

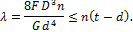
2. Определим предельное значение сил F:

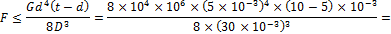
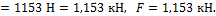
10.7. Задачи для самостоятельного решения

Задача 9.Для заданной схемы нагружения вала (рис. 10.14) построить эпюру крутящих моментов.

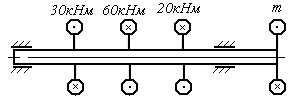
Рис. 10.14. Схема вала для построения эпюры крутящих моментов

Задача 10.Для заданного ступенчатого вала (рис. 10.15) построить эпюру крутящих моментов.

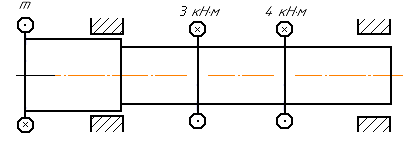
Рис. 10.15. Схема ступенчатого вала для построения эпюры

крутящих моментов

Задача 11.К валу постоянного сечения диаметром d = 50 мм (рис. 10.16) приложены моменты m₁ = 1 кНм, m₂ = 0,2 кНм, m₃ = 0,4 кНм и m₄ = 0,4 кНм. Проверить прочность вала, если [τ] = 60 МПа. Определить полный угол закручивания, если G = 8 × 10⁴ МПа.

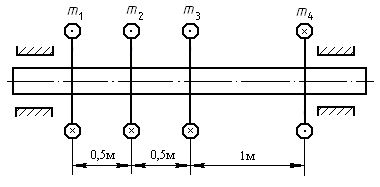
Рис. 10.16. Схема вала постоянного сечения

Ответ: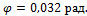

Задача 12.Цилиндрическая пружина, изготовленная из стальной проволоки диаметром d = 5 мм, растягивается силами F = 400 Н. Диаметр пружины D = 30 мм. Проверить прочность пружины, если [τ] = 500 МПа. Определить число витков пружины, при котором она удлиняется на 40 мм. G = 8 × 10⁴ МПа.

Ответ: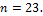

Задача 13.Определить требуемый диаметр проволоки винтовой цилиндрической пружины для осевой нагрузки F = 1,2 кН, если D/d = 6 и [τ] = 500 МПа.

Ответ: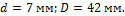

Задача 14.Для заданной схемы нагружения (рис. 10.17) определить диаметры проволоки для обеих пружин, если D₁/d₁ = D₂/d₂ = 8 и [τ] = = 600 МПа.

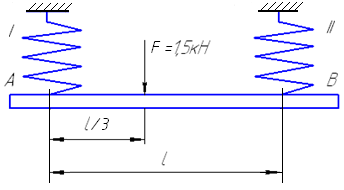
Рис. 10.17. Схема бруса, подвешенного на двух пружинах

Ответ: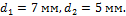

10.8. Контрольные вопросы

1. Какой вид нагружения называется кручением?

2. Что называется валом? Что такое крутящий момент?

3. Какие деформации возникают при кручении?

4. Какие внутренние силовые факторы возникают при кручении?

5. Вывести формулу для определения напряжений в поперечном сечении скручиваемого круглого вала.

6. Вывести формулы для определения относительного и полного углов закручивания круглого вала.

7. Что такое эпюра крутящего момента и как она строится?

8. Как распределяется касательное напряжение при кручении? Чему равно напряжение в центре круглого поперечного сечения?

9. Написать формулу для расчета напряжения на поверхности вала при кручении. Как изменится напряжение, если диаметр вала увеличится в два раза?

10. В чем заключается расчет на прочность при кручении?

11. В чем заключается расчет на жесткость при кручении?

12. Почему при одинаковой прочности и жесткости вал кольцевого поперечного сечения легче, чем вал сплошного круглого сечения?

13. Как вычислить потенциальную энергию деформации, накапливаемую валом при кручении?

14. Расчет статически неопределимых валов.

15. Расчет цилиндрических пружин с малым шагом витков. Что такое осадка и жесткость пружины, как они определяются?

Сложное сопротивление