Рассмотрим последний шестой участок балки. Уравнение моментов в общем виде на этом участке имеет вид

.

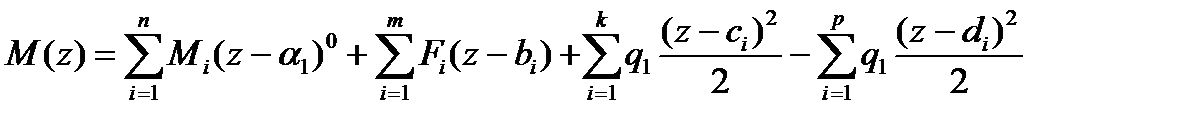Проинтегрируем дважды это уравнение, получим:

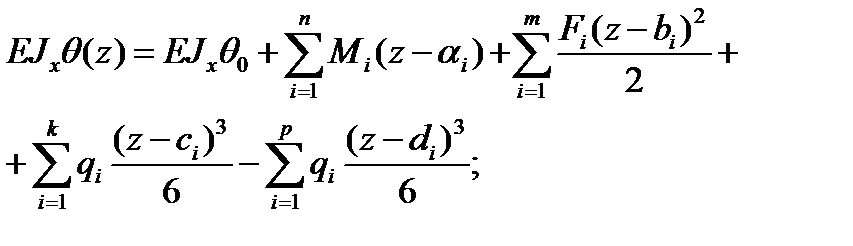
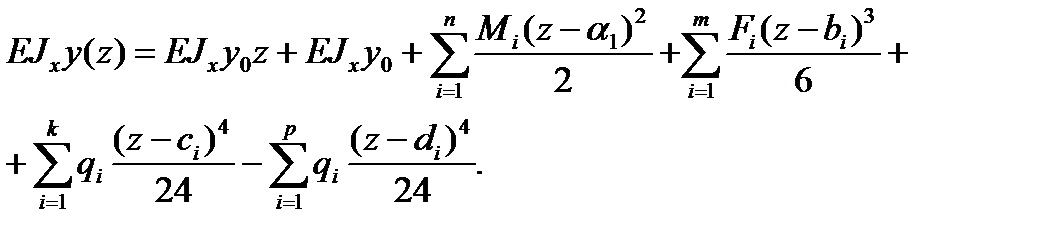
При использовании полученных уравнений должны выполняться приведенные ниже требования.

1. При определении прогиба и угла поворота произвольного сечения в уравнения записываются слагаемые только для тех нагрузок, которые расположены между началом координат и рассматриваемым сечением. Если нагрузка относительно рассматриваемого сечения создает положительный изгибающий момент, то она входит в эти уравнения со знаком «плюс».

2.Распределенная нагрузка не должна прерываться. Если по условию задачи распределенная нагрузка оканчивается на одном из участков (конец пятого участка), то ее следует продолжить до конца балки, добавив одновременно нагрузку (добавленная и компенсирующая нагрузки показаны на расчетной схеме пунктиром, рис. 9.24) такой же интенсивности, но с противоположным знаком.

3. Если начало координат расположено на левом конце балки, то положительным будет угол поворота сечения против часовой стрелки. Если же начало координат взято на правом конце балки, то положительным будет угол поворота сечения по часовой стрелке. Линейное перемещение вверх будет положительным независимо от того, где расположено начало координат.

4. Жесткость балки должна быть постоянной на всех участках.

5. Начало координат является единым для всех участков балки.

6. Ось балки является прямолинейной.

7. Значения начальных параметров находятся из граничных условий в опорных сечениях балки. Если начало координат взято в жестко закрепленном опорном сечении, то начальные параметры будут равны нулю, т. е. θ₀ = 0 и у₀ = 0. Поэтому для консольной балки, имеющей жесткую заделку, начало координат обязательно следует размещать в этом сечении.

Если начало координат находится в сечении на шарнирной опоре, то θ₀ ≠ 0 и у₀ = 0.

Если же концевые сечения балки не являются опорными сечениями, то начальные параметры не равны нулю и их необходимо определять.

Для этого в общем виде находят прогибы в опорных сечениях и, приравняв их к нулю, получают уравнения для определения начальных параметров.

Графоаналитическийметод.Интеграл Мора.

Определение перемещений и углов поворота различных сечений балки, лежащей на двух опорах, методом начальных параметров представляет собой достаточно трудоемкий процесс. Он требует громоздких вычислений по определению постоянных, интегрирования и граничных условий задачи.

Рассмотрим общий метод определения перемещений, пригодный для любой линейно деформируемой системы при любой нагрузке. Этот метод был предложен немецким ученым О. Мором.

Пусть требуется определить вертикальное перемещение у_c точки С балки, изображенной на рис. 9.25, а.

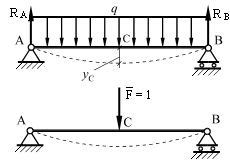
Рис. 9.25. Схема балки для определения перемещений

С помощью интеграла Мора

Возьмем такую же вторую балку (рис. 9.25, б) и в искомой точке С приложим единичную силу 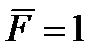. Сообщим дополнительно этой балке такие же прогибы, какие имеет первая балка, изгибаемая распределенной нагрузкой q. Потенциальная энергия U, накопленная вследствие деформации второй балки, будет равна работе единичной силы 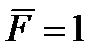на перемещении y_c:

U = 1 ∙ y_c.

Дополнительную потенциальную энергию второй балки можно определить другим способом. Если вырезать из балки бесконечно малый элемент длиной dz, то его потенциальная энергия определяется по формуле

,

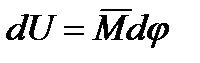где 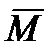– момент от единичной нагрузки 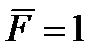в сечении С;

dφ – угол поворота концевых сечений элемента балки длиной dz,который определяется по формуле

,

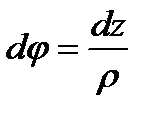где ρ – радиус нейтрального слоя.

С учетом выражения 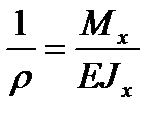, определим dφ:

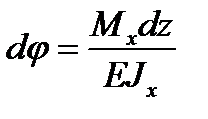, далее .

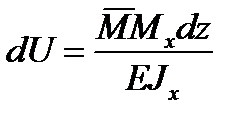Потенциальная энергия всей балки, нагруженной единичной силой, определится по формуле

.

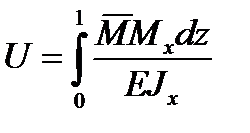Сравним выражения для определения потенциальной энергии, найденной двумя способами, получим:

.

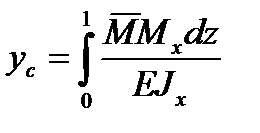Если балка имеет постоянное поперечное сечение, то

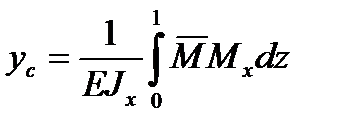– интеграл Мора,

где y_c – прогиб балки в рассматриваемом сечении;

ЕJ_x – жесткость балки при изгибе;

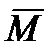– изгибающий момент в рассматриваемом сечении от действия

единичной силы;

М_х – изгибающий момент в рассматриваемом сечении от действия

на балку внешних нагрузок;

z – координата сечения балки.

Для определения угла поворота в рассматриваемом сечении прикладываем единичный момент 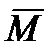= 1.

Способ Верещагина.

Помимо непосредственного вычисления интеграла Мора для определения перемещений при изгибе можно пользоваться графоаналитическим методом перемножения эпюр по правилу Верещагина.

Для вывода формулы, предложенной Верещагиным, возьмем участок балки длиной l₁–l₂. Построим грузовую эпюру M от заданной внешней нагрузки. Часть грузовой эпюры на длине балки l₁–l₂ показана на рис. 9.26, а.

В сечении С, где необходимо определить прогиб балки, прикладываем единичную силу 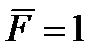и строим от нее единичную эпюру изгибающих моментов 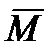. Часть этой эпюры на той же длине балки приведена на рис. 9.26, б.

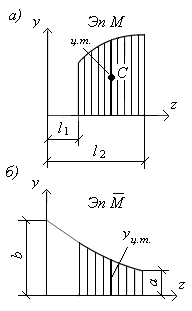
Рис. 9.26. Схема участка балки

для определения перемещений

способом Верещагина

В общем случае грузовая эпюра определяется уравнением М = f(x), а эпюра от единичной нагрузки – уравнением прямой линии = аz + b. Подставим эти значения в интеграл Мора, получим:

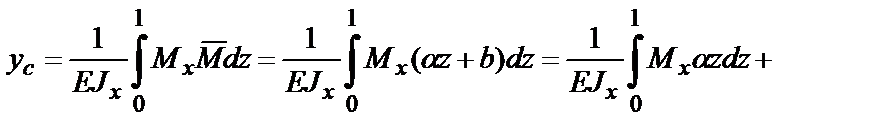
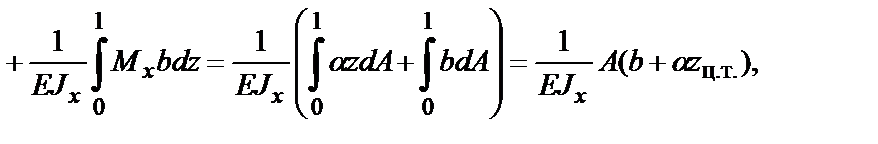
где А – площадь грузовой эпюры на участке балки длиной dz.

Так как b + αz_ц.т = γ_ц.т, то окончательно получим:

,

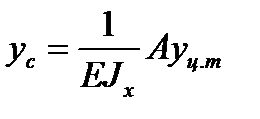где у_ц.т – ордината единичной эпюры моментов 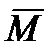под центром тяжес-

ти грузовой эпюры М_х.

Для нескольких грузовых участков балки формула перемещений имеет вид:

.

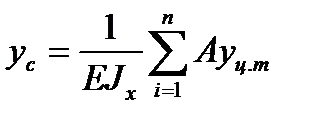Для определения перемещений при помощи правила Верещагина необходимо:

1) построить эпюры изгибающих моментов от внешней нагрузки.

В том сечении, где необходимо определить прогиб, приложить единичную силу (для нахождения угла поворота в сечении приложить единичный момент);

2) построить эпюры изгибающих моментов от единичной силы (от единичного момента);

3) вычислить площадь эпюры А на каждом участке балки.

Умножить каждую площадь грузовой эпюры на соответствующую ординату единичной эпюры, находящуюся под центром тяжести грузовой эпюры.

Полученные результаты сложить.

При этом необходимо учитывать следующее: перемножение эпюр с одинаковыми знаками дает знак «плюс», с разными знаками – «минус».

Положительные перемещения у_си θ_с всегда направлены в сторону действия соответствующей им единичной силы или единичного момента.

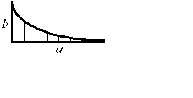
Для упрощения процесса расчета деформаций балки целесообразно воспользоваться готовой таблицей, где приведены формулы, по которым можно найти произведение Ау_ц.т в зависимости от вида эпюр М_х и 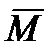(табл. 9.1).

Т а б л и ц а 9.1. Значения Ау_ц.т, используемые при применении правила

Верещагина

Эпюры Mx, построенные от внешних нагрузок	Эпюры , построенные от единичных сил и моментов
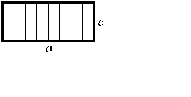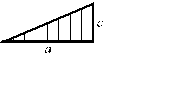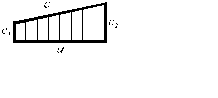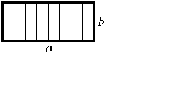	abc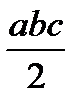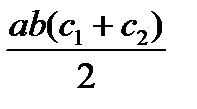

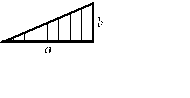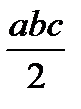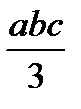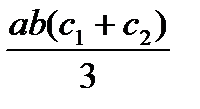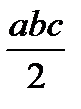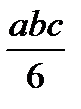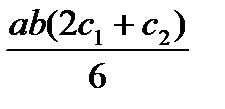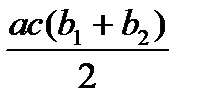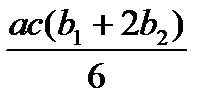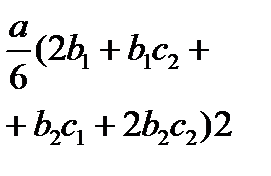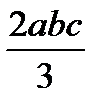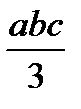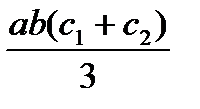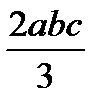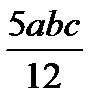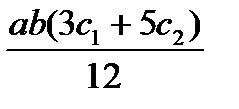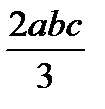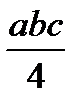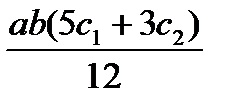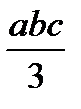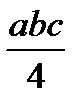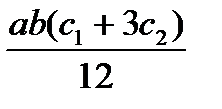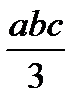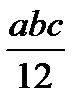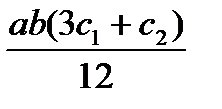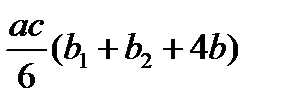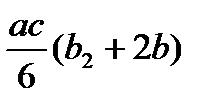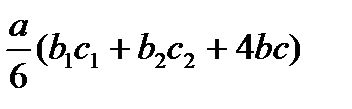9.11. Балки переменного сечения. Определение деформаций

Размеры балок с постоянным поперечным сечением определяются по максимальному изгибающему моменту в опасном сечении, в остальных же сечениях балка имеет лишний запас прочности. Поэтому на практике широко распространены балки, поперечное сечение которых изменяется по длине. Кроме того, по конструктивным соображениям балки, работающие на изгиб, часто имеют отверстия, выточки, ступени, конусность и т. д.

С точки зрения расчета на прочность и жесткость все такие балки можно разделить на три основные группы:

балки, имеющие местные изменения формы и размеров сечений (рис. 9.27, а);

балки ступенчато-переменного сечения (рис. 9.27, б);

балки, имеющие непрерывно изменяющиеся по длине размеры сечений (рис. 9.27, в).

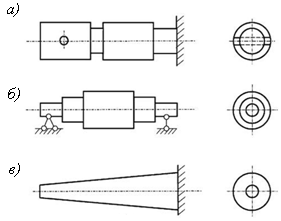
Рис. 9.27. Схемы балок с переменным сечением по длине

Отверстия, выточки и прочие нарушения формы и размеров сечений вызывают резкое и значительное изменение закона распределения напряжений и деформаций. Однако это изменение носит местный характер и на прочность стержня в большинстве случаев влияет незначительно. Поэтому условие прочности записывают для опасной точки, расположенной в одном из ослабленных сечений, так как здесь может иметь место концентрация напряжений. В зависимости от чувствительности материала к концентрации напряжений условия прочности будут иметь различный вид.

Для пластичных материалов (малоуглеродистая сталь, медь, алюминий) и хрупких неоднородных материалов (чугун) концентрация напряжений не учитывается и условие прочности записывается в обычном виде:

.

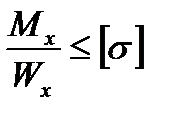Для однородных хрупких материалов (высокопрочная закаленная сталь) концентрацию напряжений необходимо учитывать. Для таких материалов условие прочности имеет вид

,

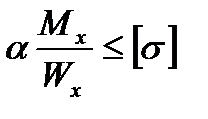где а – теоретический коэффициент концентрации напряжений, опреде-

ляемый по справочным таблицам.

При определении прогибов и углов поворота сечений отверстия и прочие нарушения формы и размеров сечения не учитывают.

В местах сопряжения участков с различными размерами поперечных сечений возникает концентрация напряжений. Если материал чувствителен к ней, то необходимо применять второе условие прочности ко всем сечениям на границах участков балки. Если же материал нечувствителен к концентрации напряжений, то следует применить первое условие прочности к нескольким вероятным опасным сечениям.

Для определения перемещений в ступенчатом стержне можно пользоваться методом непосредственного интегрирования дифференциального уравнения упругой линии балки или энергетическими методами, которые будут рассмотрены ниже, или применять видоизмененный метод начальных параметров. Суть последнего заключается в замене ступенчатого стержня эквивалентным ему по деформациям стержнем постоянной жесткости.

Частным случаем балок с непрерывно меняющимися по длине размерами сечений являются балки равного сопротивления изгибу. В таких балках во всех сечениях максимальные нормальные напряжения одинаковы и равны допускаемым напряжениям, т. е.

,

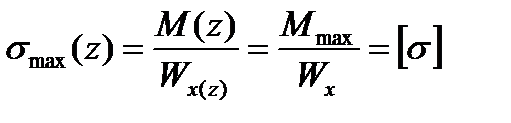отсюда

.

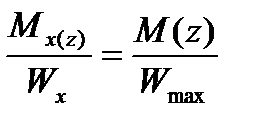Рассмотрим балку равного сопротивления изгибу на примере.

Балка прямоугольного сечения одним концом защемлена в заделку, на ее свободном конце приложена сосредоточенная сила F (рис. 9.28, а).

Изгибающий момент в произвольном сечении, расположенном на расстоянии z от свободного конца балки:

M(z) = –Fz.

.

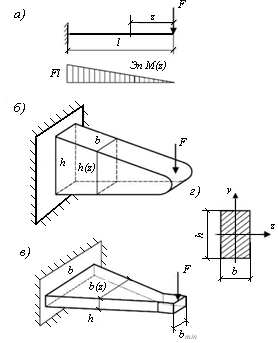
Рис. 9.28. Схема балки равного сопротивления изгибу по длине

В заделке M_max = –Fl, при ширине сечения в заделке b и высоте h,

.

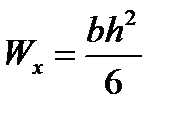Рассмотрим частный случай, когда ширина сечения b = const, а высота сечения h = h(z). В этом случае

,

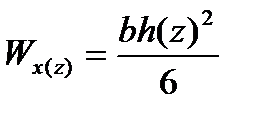тогда

,

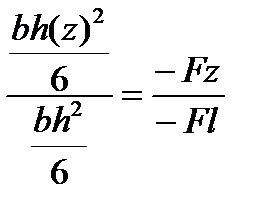откуда

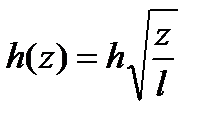
Из полученного выражения можно сделать вывод, что высота сечения балки равного сопротивления изгибу с постоянной шириной сечения меняется по закону параболы (рис. 9.28, б). Таким образом, определив высоту h в опасном сечении, можно определить и высоту h(z) в любом сечении балки.

Так как площадь параболы составляет 2/3 от площади описанного прямоугольника длиной l и высотой h, то объем балки равного сопротивления изгибу будет составлять 2/3 от объема балки с постоянным сечением bh. Таким образом,экономия материала составит 33 %.

Рассмотрим другое решение этой задачи, когда высота сечения h = const, а ширина сечения b = b(z). В этом случае имеем:

,

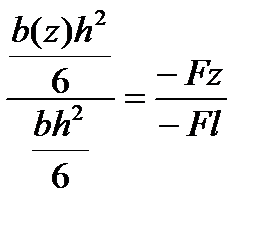откуда

.

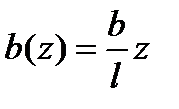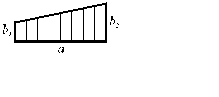
Следовательно, в этом случае ширина балки изменяется по линейному закону. Получить форму такой балки не представляет больших затруднений (рис. 9.28, в).

Экономия материала при применении такой балки в сравнении с призматической балкой, имеющей сечение bh, достигает 50 %. Ширина концевого сечения балки определяется из условия прочности по касательным напряжениям:

,

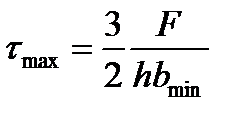Откуда

.

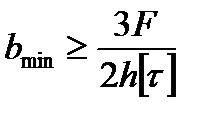Определим наибольший прогиб этой балки. Момент инерции произвольного сечения относительно оси z (рис. 9.28, г) определяется по формуле

,

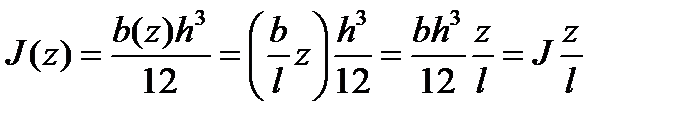где J – момент инерции сечения в заделке.