Моменты сопротивления сечений

Моментом сопротивления сечения называется геометрическая характеристика, величина которой определяется по формулам:

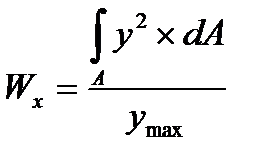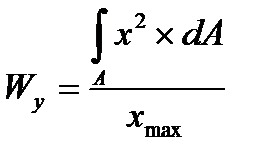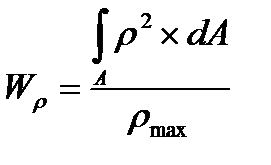, , – осевые и полярный моменты сопротивления сечения соответственно,

где у_max, x_max, r_max – расстояние от наиболее удаленной точки сечения до соответствующей оси.

Определим моменты сопротивления простых сечений относительно центральных осей.

1. Прямоугольник:

,

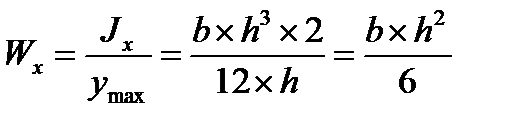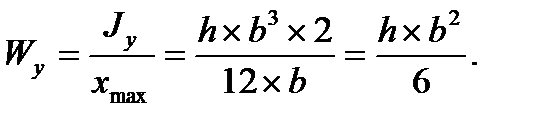
2. Момент сопротивления треугольника относительно центральной оси, параллельной основанию (см. рис. 5.6):

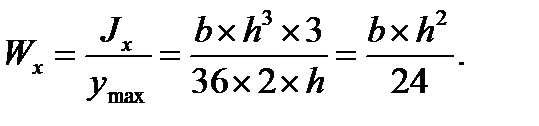
3. Круг:

,

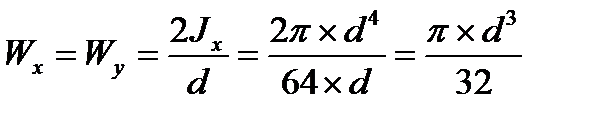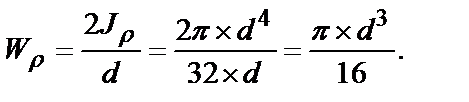
Пример расчета

Задача 1. Определить главные центральные моменты инерции и положение главных центральных осей инерции сечения (рис. 5.10).

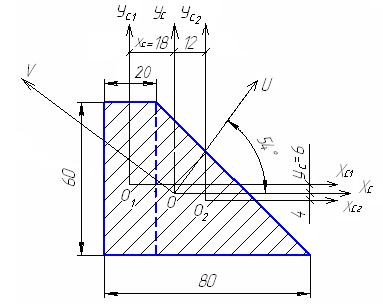
Рис. 5.10. Схема составного сечения

Решение.

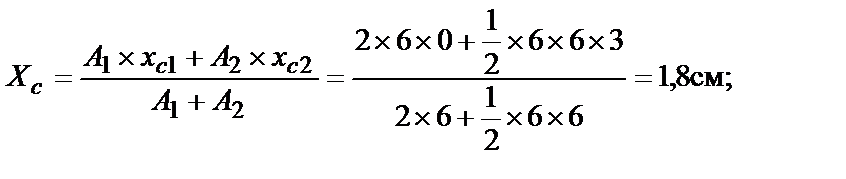
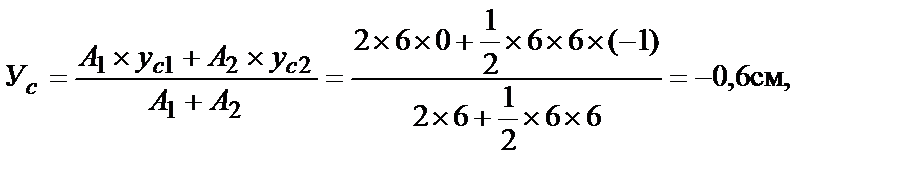
где А₁ = 2×6 = 12 см² – площадь прямоугольника;

А₂ = 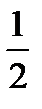× 6 × 6 = 18 см² – площадь треугольника;

х_с1 = у_с1 = 0, х_с2 = 3 см, у_с2 = –1 см – расстояние от центра тяжести прямоугольника и треугольника до осей у_с1 и х_с1 соответственно.

1. Определяем моменты инерции составного сечения относительно центральных осей Х_с и У_с:

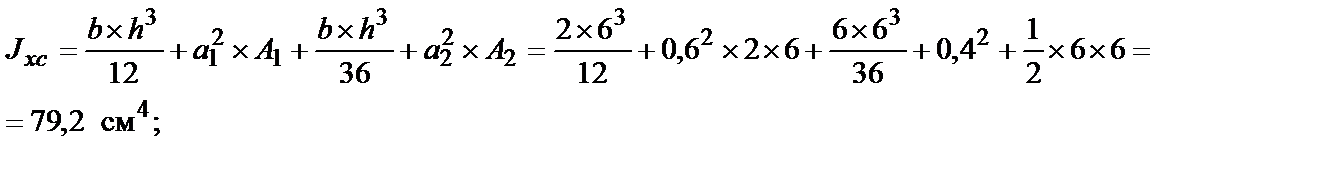
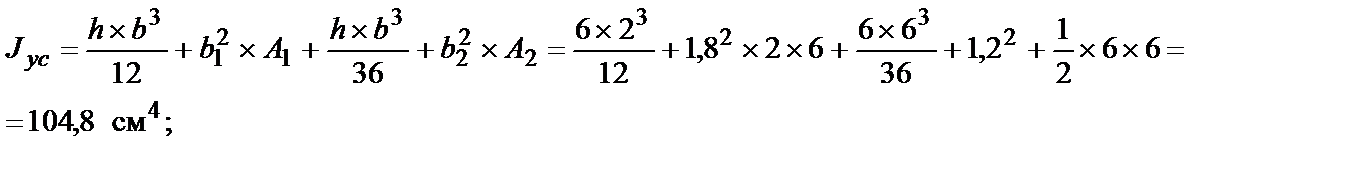
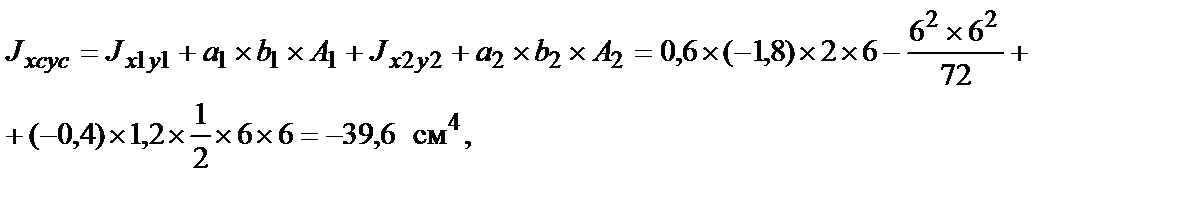где J_{xcy c} = 0 – центробежный момент инерции прямоугольника относи-

тельно собственных осей;

J_x2y2 = 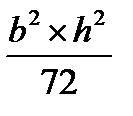– центробежный момент инерции прямоугольного

треугольника относительно собственных осей;

a₁ = 0,6 см, b₁ = –1,8 см, а₂ = –0,4 см, b₂ = 1,2 см – расстояния от собственных осей прямоугольника и треугольника до осей Х_с и У_с соответственно.

2. Определяем главные центральные моменты инерции составного сечения:

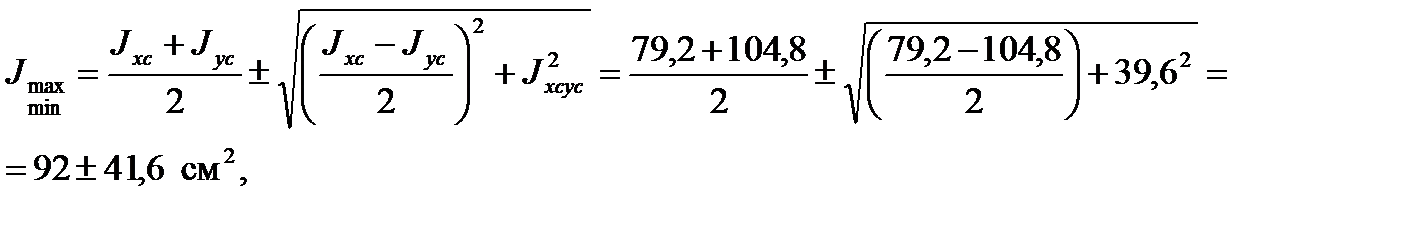откуда

J_max = J_u = 92 + 41,6 = 133,6 см⁴;

J_min = J_n = 92 – 41,6 = 50,4 см⁴.

3. Определяем положение главных центральных осей:

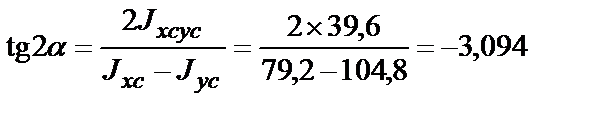; a = –36;

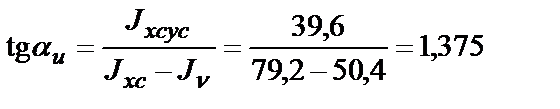; a_u = 54.

Задача 2. Определить главные центральные моменты инерции сечения, изображенного на рис. 5.11.

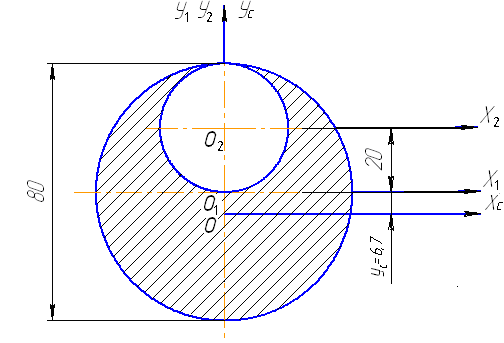
Рис. 5.11. Схема составного сечения

Решение. 1. Определяем положение центра тяжести составного сечения относительно осей Х₁и У₁:

;

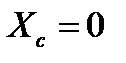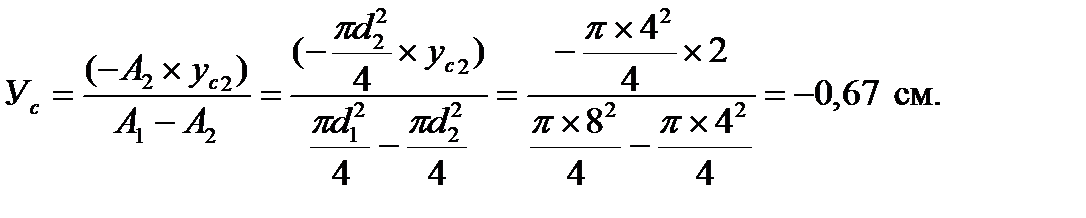
2. Определяем моменты инерции составного сечения относительно центральных осей:

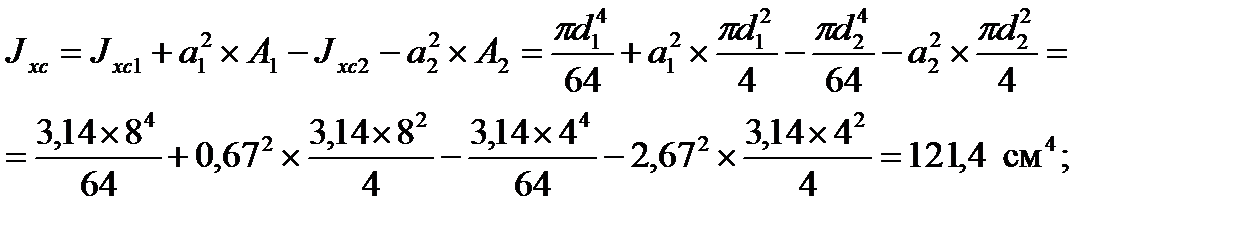
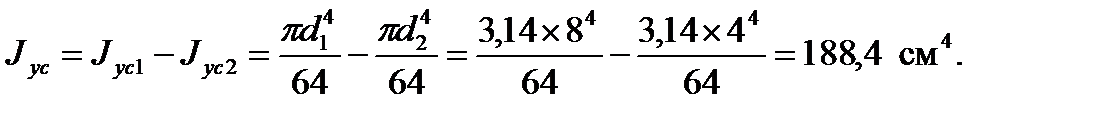
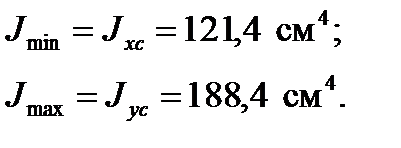
Задача 3. Для составного сечения из швеллера № 14 и равнобокого уголка № 5 (рис. 5.12) требуется:

1) определить положение центра тяжести;

2) найти величину осевых и центробежных моментов инерции относительно центральных осей;

3) определить направление главных центральных осей;

4) найти величину моментов инерции относительно главных центральных осей.

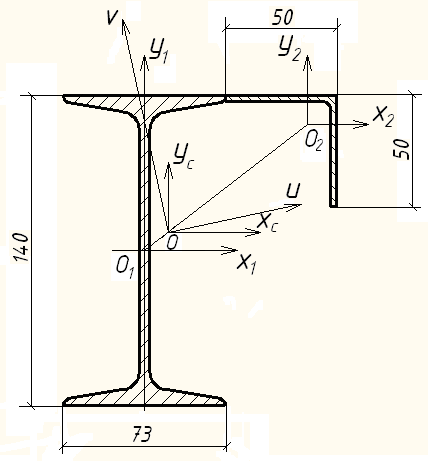
Рис. 5.12. Схема составного сечения

из прокатных профилей

Решение. Из сортаментов значений размеров и геометрических характеристик сечений (прил. 1–4):

для двутавра № 14: h₁ = 140 мм; b₁ = 73 мм; d₁ = 4,9 мм; A₁ = = 17,4 см²; J_x = 572 см⁴; S_x = 46,8 см³; J_y = 41,9 см⁴;

для уголка № 5: b₂ = 50 мм; d₂ = 3 мм; A₂ = 2,6 см²; J_x = 7,11 см⁴;
J_max = 11,3 см⁴; J_min = 2,95 см⁴; x _c = у_с = 1,33 см.

1. Определяем положения центра тяжести составного сечения относительно центральных осей Х₁ и У₁ двутавра.

Относительно них статические моменты двутавра равны нулю, поэтому:

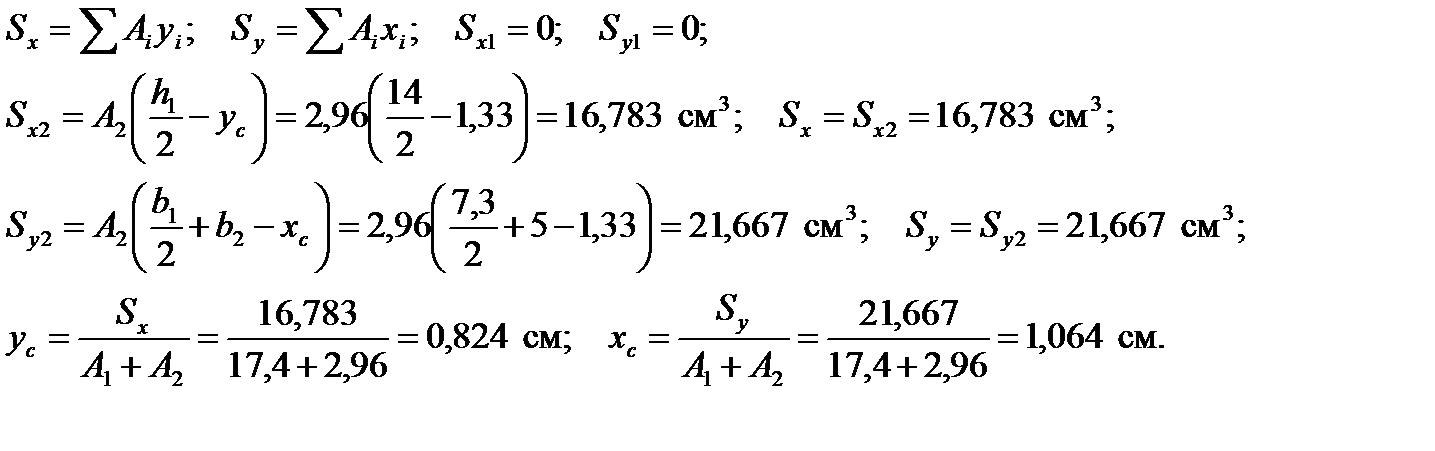
2. Находим величину осевых и центробежных моментов инерции относительно центральных осей:

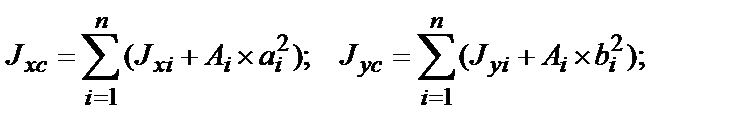
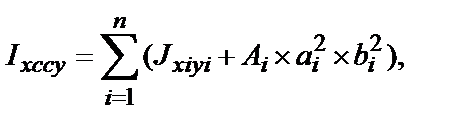
где а_i – расстояние между осями Х_с и Х_i;

b_i – расстояние между осями У_c и У_i.

Для двутавра:

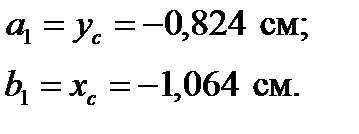
Для уголка:

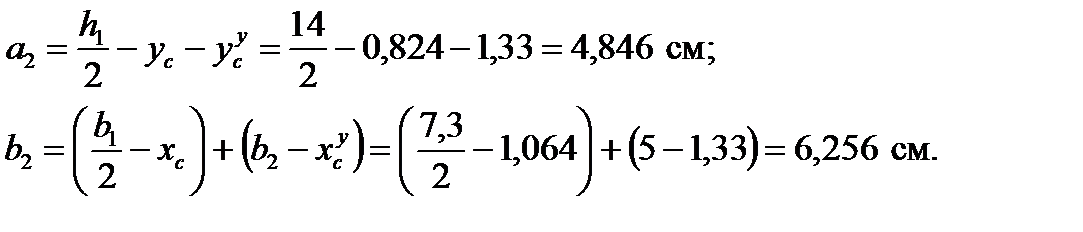
Находим осевые моменты относительно оси X_c:

для двутавра:

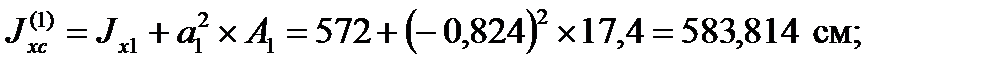
для уголка:

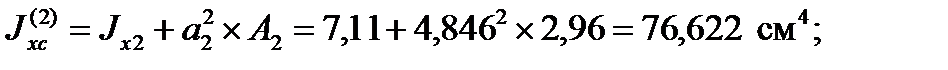
для всего сечения:

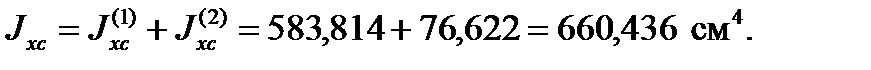
Осевые моменты инерции относительно оси У_c:

для двутавра:

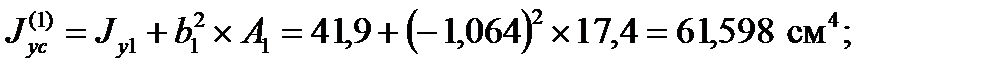
для уголка:

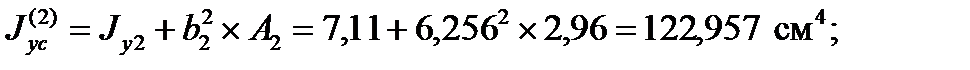
для всего сечения:

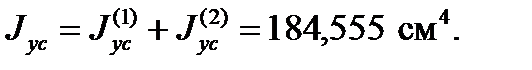
Определяем центробежный момент инерции относительно осей X_c, Y_c:

для двутавра:

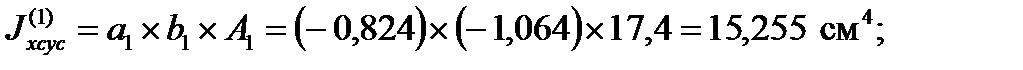
для уголка:

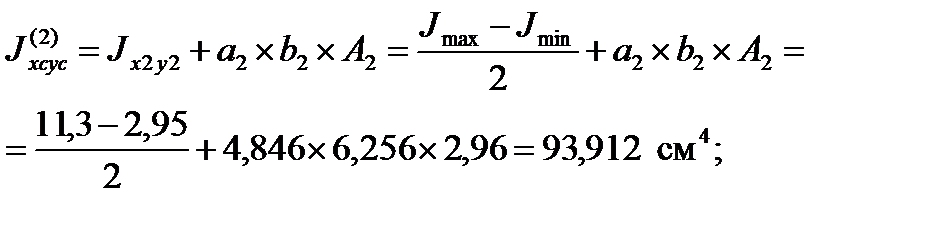
для всего сечения:

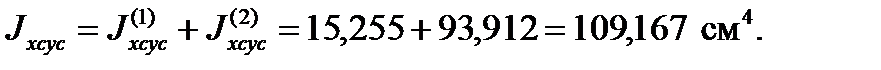
3. Определяем направление главных центральных осей:

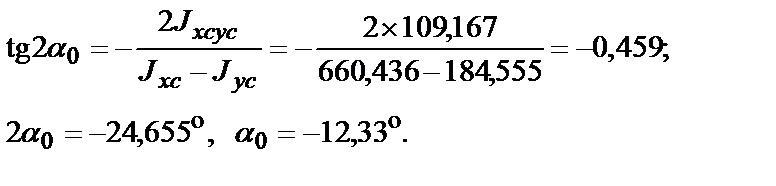
Положительному углу соответствует поворот по часовой стрелке, поэтому оси UV следует повернуть против часовой стрелки на угол 12,33^° относительно осей X_c и Y_c.

4. Находим величину моментов инерции относительно главных центральных осей:

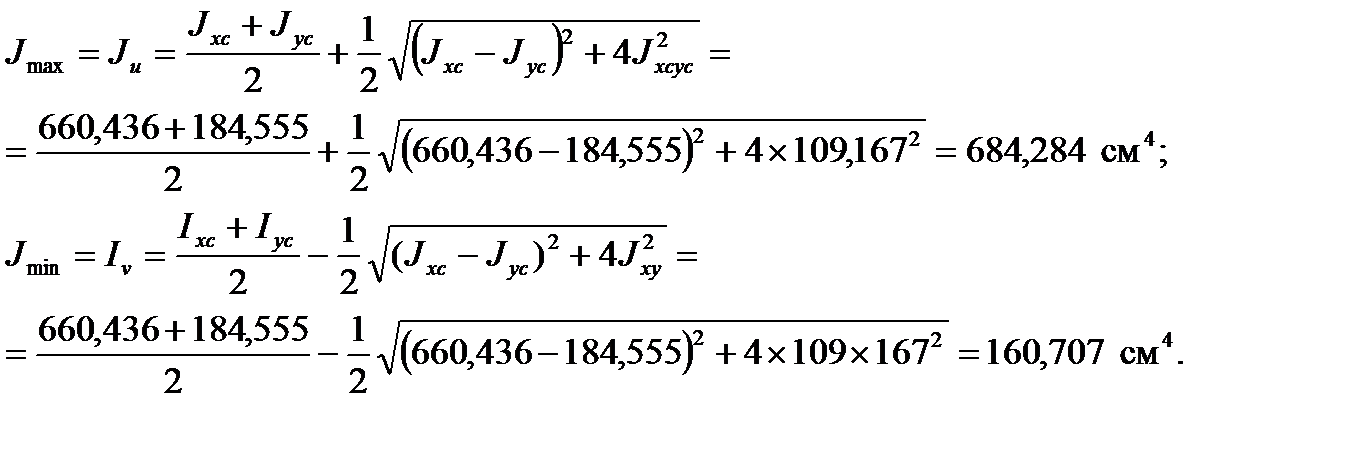
5.11. Задачи для самостоятельного решения

Задача 4.Определить главные центральные моменты инерции сечения (рис. 5.13).

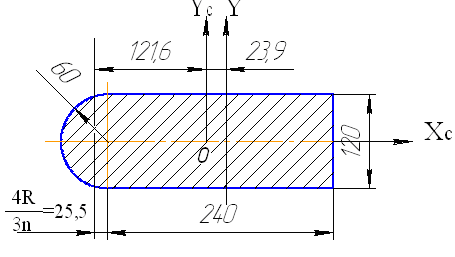
Рис. 5.13. Схема составного сечения

Ответ: J_min = 3965 см⁴; J_max = 23827 см⁴.

Задача 5.Определить главные центральные моменты инерции сечений (рис. 5.14).

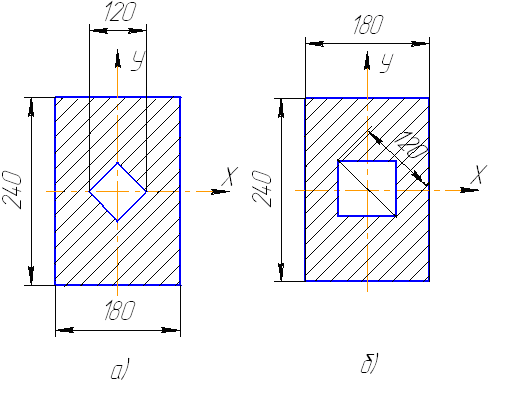
Рис. 5.14. Схемы составных сечений

Ответ: J_min = 11232 см⁴; J_max = 20304 см⁴.

Задача 6.Вычислить центробежный момент инерции неравнобокого уголка 100 × 63 × 8 относительно центральных осей, параллельных полкам (рис. 5.15).

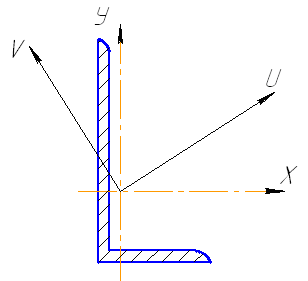
Рис. 5.15. Схема неравнобокого уголка

Ответ: J_xy = –40,5 см⁴.

5.12. Контрольные вопросы

1. Что называется статическим моментом площади сечения относительно оси, в каких единицах он выражается?

2. Что такое осевой, центробежный и полярный моменты инерции? В каких единицах выражаются моменты инерции сечения?

3. Чему равен статический момент площади относительно оси, проходящей через центр тяжести сечения?

4. Как определяются координаты центра тяжести простых (квадрат, прямоугольник, круг) и сложных сечений?

5. Чему равен осевой момент инерции прямоугольника относительно центральной оси, параллельной одной из его сторон?

6. Как изменяются осевые моменты инерции при параллельном переносе и повороте осей?

7. Какие оси называются главными осями инерции?

8. Какие оси называются главными центральными осями инерции?

9. Чему равен центробежный момент инерции относительно главных осей инерции?

10. В каких случаях можно без вычисления установить положение главных осей?

11. Как определить положение главных центральных осей инерции?

12. Сколько в сечении можно провести центральных и главных центральных осей инерции?

СДВИГ

Основные понятия о деформации сдвига.