Инерции сечения. Общие свойства

Осевым моментом инерции сечения относительно какой-либо оси называется взятая по всей площади Асечениясумма произведений площадей элементарных площадок на квадраты их расстояний до взятой оси (см. рис. 5.1), что выражается следующими интегралами:

,

Геометрическая характеристика, которая представляет собой взятую по всей площади Асечениясумму произведений площадей элементарных площадок на произведение их расстояний до двух данных взаимно перпендикулярных осей (см. рис. 5.1), называется центробежным моментом инерции сечения относительно осей х иу и определяется по формуле

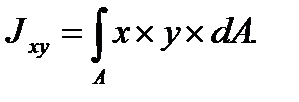
Полярным моментом инерции сечения относительно начала системы координат хОу называется геометрическая характеристика, величина которой определяется равенством

,

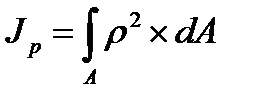где r – расстояние от начала координат до элементарной площадки dA.

Согласно рис. 5.1 имеем:

,

тогда

,

Таким образом, сумма осевых моментов инерции сечения относительно двух взаимно перпендикулярных осей равна полярному моменту инерции сечения относительно точки пересечения этих осей.

Общие свойства моментов инерции:

1) размерность моментов инерции [L⁴];

2) осевые и полярный моменты инерции всегда положительны. Центробежный момент инерции может быть положительным, отрицательным или равняться нулю.

Изменение моментов инерции при параллельном переносе

И повороте осей

Пусть моменты инерции J_x, J_y и J_xy для заданного сечения относительно старых осей x и y известны. Возьмем новую систему координат x₁О₁y₁(рис. 5.2), оси которой параллельны старым осям. Обозначим через а и b координаты точки О₁. Рассмотрим элементарную площадку dA, координаты которой в старой системе координат хОу равны x иy. В новой системе координат x₁О₁y₁ они равны x₁= x – b и y₁= y – a.

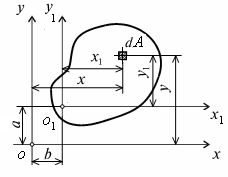
Рис. 5.2. Схема для определения моментов инерции

сечения при параллельном переносе осей

Подставим значение y₁ = y – a в выражение осевого момента инерции относительно оси x₁, получим:

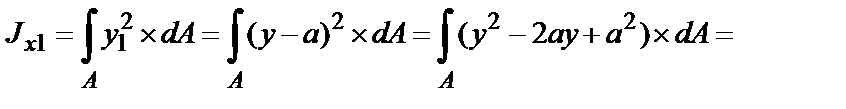
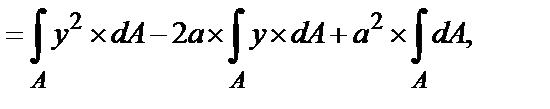
окончательно получим

Аналогично найдем

Подставляя значения х₁= x – b и y₁= y – a в выражение

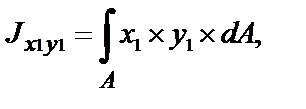
получим формулу для определения центробежного момента инерции сечения относительно осей х₁и у₁:

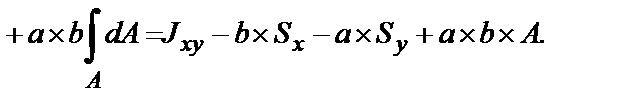
Если оси х и у проходят через центр тяжести сечения и совпадают с центральными осями х_с и у_с, то статический момент S_x = S _y= 0. Формулы для определения моментов инерции относительно осей х₁и у₁ принимают вид:

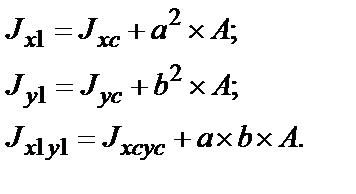
Моменты инерции сечения сложной формы относительно любых осей определяются как сумма моментов инерции составляющих (простых) частей сечения относительно этих осей.

Относительно оси х:

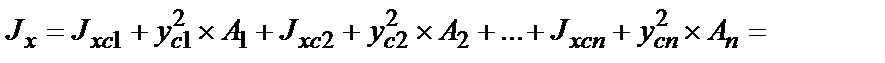
относительно оси у:

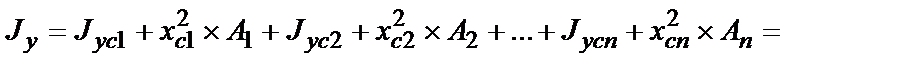
где J_xciyci – центробежный момент инерции i-й части сечения относи-

тельно осей х_сi и y_ci, проходящих через ее центр тяжести параллельно осям х и y;

у_сi – расстояние между осями х_сi и х;

х_сi – расстояние между осями y_ci и у.

Возьмем новую систему координат x₁Оy₁с началом в той же точке О, но повернутую относительно старой системы хОу на угол a (рис. 5.3). Угол a считаем положительным, если поворот на этот угол оси х до совмещения с осью х₁ выполнен против часовой стрелки.

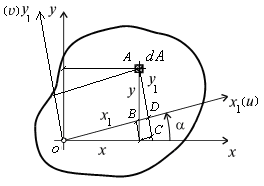
Рис. 5.3. Схема для определения моментов

инерции сечения при повороте осей

Рассмотрим элементарную площадку dAс координатами xиy в старой системе координат. Определим координаты x₁и y₁этой площадки в системе координат x₁Оy₁. Из рис. 5.3 имеем: x₁ = OB + BD, OB = x ´ cos α, BD = y ´ sin α, аналогично y₁ = AC – DC, AC = y ´ cos α, DC = x ´ sin α, окончательно получим:

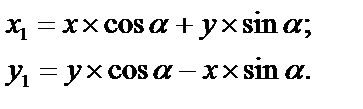
Подставим эти значения в формулы

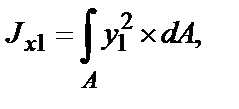
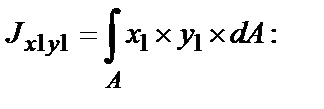
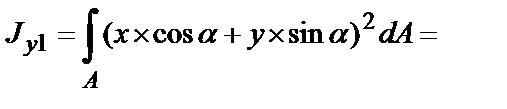
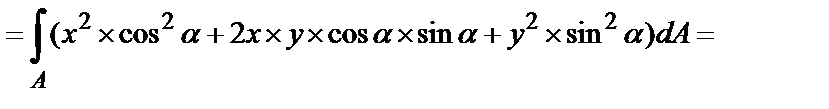
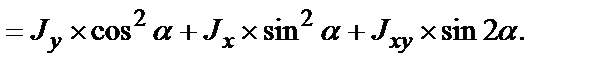
Если сложить моменты инерции относительно осей x₁и y₁, то получим

J_x1 + J_у1 = J_x + J_у = сonst.

Следовательно, сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей сохраняет постоянную величину при их повороте на любой угол.

При определении моментов инерции использовались следующие формулы: