Признаки монотонности функции.
Теорема 1. Для того чтобы дифференцируемая на интервале функция возрастала (убывала) на этом интервале, необходимо и достаточно, чтобы ее производная была во всех точках интервала неотрицательна (неположительна). Если производная функция во всех точках интервала положительна (отрицательна), то функция строго возрастает (строго убывает).
 Докажем, например, что если на интервале (a,b) производная функции f неотрицательна (f'(x) > 0 для всех x
Докажем, например, что если на интервале (a,b) производная функции f неотрицательна (f'(x) > 0 для всех x 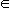 (a,b)), то функция f возрастает на (a,b). Действительно, если x1
(a,b)), то функция f возрастает на (a,b). Действительно, если x1 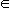 (a,b), x2
(a,b), x2 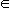 (a,b) и x1 < x2, то по теореме Лагранжа
(a,b) и x1 < x2, то по теореме Лагранжа
f(x2) - f(x1) = f'( 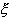 )(x2 - x1), x1 < )(x2 - x1), x1 < 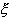 < x2, < x2, | (15.1) |
а так как по условию f'( 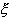 ) > 0, то из равенства (15.1) следует, что f(x2) - f(x1) > 0, т. e.
) > 0, то из равенства (15.1) следует, что f(x2) - f(x1) > 0, т. e.
| f(x1) < f(x2). | (15.2) |
При этом если для всех x 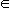 (a,b) выполняется неравенство f'(x) > 0 и, следовательно, в равенстве (15.1) f'(
(a,b) выполняется неравенство f'(x) > 0 и, следовательно, в равенстве (15.1) f'( 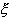 ) > 0, то f(x2) - f(x1) > 0, т. е.
) > 0, то f(x2) - f(x1) > 0, т. е.
| f(x1) < f(x2) | (15.3) |
- функция f строго возрастает.
Пусть теперь функция f возрастает на интервале (a,b) и имеет в точке x0 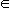 (a,b) производную. Возьмем
(a,b) производную. Возьмем
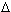 x > 0, тогда
x > 0, тогда
f(x0 +  x) > f(x0)
x) > f(x0)
и, следовательно,
(f(x0 +  x)- f(x0))/ x)- f(x0))/  x > 0 x > 0 | (15.4) |
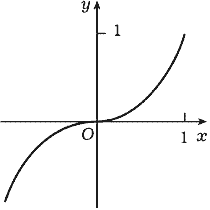 Рис. 82 Рис. 82 |
Переходя в этом неравенстве к пределу при  x
x 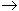 0, получим
0, получим
| f'(x0) > 0. | (15.5) |
Аналогично теорема 1 доказывается для убывающих функций. 
Замечание 1. Как было показано, условие положительности производной на интервале является достаточным условием строгого возрастания. Отметим, что это условие не является, однако, необходимым условием строгого возрастания. Действительно, например, функция f(x) = x3 строго возрастает на всей числовой оси, однако ее производная f'(x) = 3x2 не всюду положительная - она обращается в нуль при x = 0 (рис. 82).
36. Экстремум функции одной переменной.
Опр.Функция 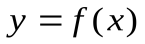 называетсядифференцируемой в данной точке
называетсядифференцируемой в данной точке 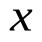 , если приращение
, если приращение 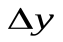 этой функции в точке
этой функции в точке 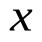 , соответствующее приращению аргумента
, соответствующее приращению аргумента 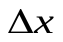 , может быть представлено в виде
, может быть представлено в виде 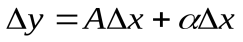 ,(9)
,(9)
где 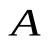 - некоторое число, не зависящее от
- некоторое число, не зависящее от 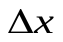 , а
, а 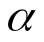 – функция аргумента
– функция аргумента 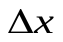 , являющаяся бесконечно малой при
, являющаяся бесконечно малой при 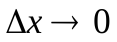 .
.
Заметим, что функция 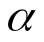 (
( 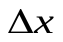 ) может принимать в точке
) может принимать в точке 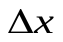 =0 какое угодно значение. Ради определенности можно положить
=0 какое угодно значение. Ради определенности можно положить 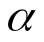 (0)=0 (при этом частное значение функции
(0)=0 (при этом частное значение функции 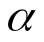 (
( 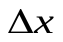 ) в точке
) в точке 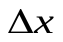 =0 будет совпадать с ее предельным значением в этой точке).
=0 будет совпадать с ее предельным значением в этой точке).
Так как произведение двух бесконечно малых 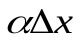 является бесконечно малой более высокого порядка, чем
является бесконечно малой более высокого порядка, чем 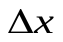 , т.е.
, т.е. 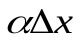 =0(
=0( 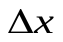 ), то формулу (9) можно переписать в виде
), то формулу (9) можно переписать в виде 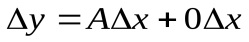 .
.
Пусть функция 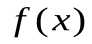 определена всюду в некоторой окрестности точки
определена всюду в некоторой окрестности точки 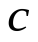 .
.
Опр.Говорят, что функция 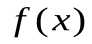 имеет в точке
имеет в точке 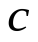 локальный максимум (минимум), если найдется такая окрестность точки
локальный максимум (минимум), если найдется такая окрестность точки 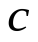 , в пределах которой значение
, в пределах которой значение 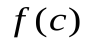 является наибольшим (наименьшим) среди всех значений этой функции.
является наибольшим (наименьшим) среди всех значений этой функции.
На рис.1 изображена функция 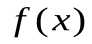 , имеющая локальный максимум в точке
, имеющая локальный максимум в точке 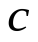 .
.
Локальный максимум и локальный минимум объединяются общим названием локальный экстремум.
Теоремы0( о достаточном условии возрастания (убывания) функции 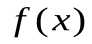 в точке
в точке 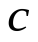 ):если функция
):если функция 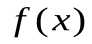 дифференцируема в точке
дифференцируема в точке 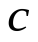 и
и 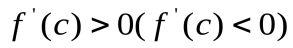 , то эта функция возрастает (убывает) в точке
, то эта функция возрастает (убывает) в точке 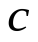 .
.
Опр.Говорят, что функция 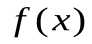 возрастает (убывает) в точке
возрастает (убывает) в точке 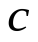 , если найдется такая окрестность точки
, если найдется такая окрестность точки 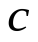 , в пределах которой
, в пределах которой 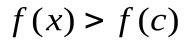 при
при 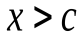 и
и 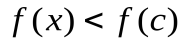 при
при 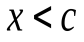 (
( 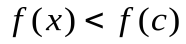 при
при 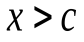 и
и 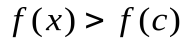 при
при 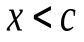 ).
).
37. Наибольшее и наименьшее значения функции.
Если функция 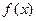 непрерывна на замкнутом отрезке xÎ[a;b], то она обязательно имеет на этом отрезке наименьшее и наибольшее значения (это одно из свойств функций, непрерывных на замкнутом отрезке):
непрерывна на замкнутом отрезке xÎ[a;b], то она обязательно имеет на этом отрезке наименьшее и наибольшее значения (это одно из свойств функций, непрерывных на замкнутом отрезке): 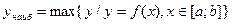 ,
, 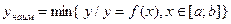 . Эти значения достигаются функцией либо в точках экстремумов внутри отрезка, либо на концах отрезка.
. Эти значения достигаются функцией либо в точках экстремумов внутри отрезка, либо на концах отрезка.
Правило практического нахождения наименьшего и наибольшего значений функции на отрезке 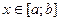 :
:
1) найти критические точки функции на интервале 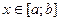 ;
;
2) вычислить значения функции в найденных критических точках;
3) вычислить значения функции на концах отрезка, то есть в точках х = a и х = b;
4) среди всех вычисленных значений функции выбрать наибольшее и наименьшее.
Если функция 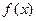 на отрезке xÎ[a;b], имеет лишь одну критическую точку и она является точкой максимума (минимума), то в этой точке функция принимает наибольшее (наименьшее) значение.
на отрезке xÎ[a;b], имеет лишь одну критическую точку и она является точкой максимума (минимума), то в этой точке функция принимает наибольшее (наименьшее) значение.
Пример 1. Найти наибольшее и наименьшее значение функции 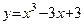 на отрезке хÎ[–2;3].
на отрезке хÎ[–2;3].
Решение. Так как 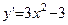
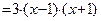 , то критическими точками функции являются х1 = –1 и х2 = 1 и они обе принадлежат отрезку
, то критическими точками функции являются х1 = –1 и х2 = 1 и они обе принадлежат отрезку
[–2; 3]. Сравнивая значения функции в этих точках и значения функции на концах заданного отрезка
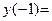 5,
5, 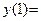 1,
1,  1,
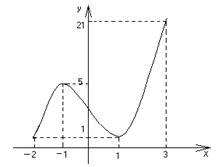
1, 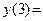 21, заключаем, что наименьшее значение функции равно 1 и достигается в точке х = –2 и х = 1, а наибольшее значение функции равно 21 и достигается в точке х = 3. Все полученные результаты хорошо иллюстрируются схематичным графиком на заданном отрезке.
21, заключаем, что наименьшее значение функции равно 1 и достигается в точке х = –2 и х = 1, а наибольшее значение функции равно 21 и достигается в точке х = 3. Все полученные результаты хорошо иллюстрируются схематичным графиком на заданном отрезке.
Ответ: 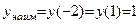 ,
, 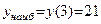 .
.
Пример 2. 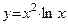 , хÎ[1;е]. Найти
, хÎ[1;е]. Найти 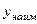 и
и 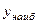 . Решение.
. Решение.
Во всех точках заданного замкнутого отрезка данная функция определена и непрерывна, имеет производную 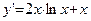
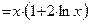
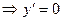 , если
, если 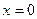 или
или 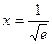 . Обе стационарные точки х1 = 0 и х2
. Обе стационарные точки х1 = 0 и х2 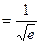 не принадлежат отрезку [1; е]. Поэтому, внутри заданного отрезка нет критических точек (то есть функция на нем сохраняет монотонность). Остается вычислить значение функции на концах отрезка:
не принадлежат отрезку [1; е]. Поэтому, внутри заданного отрезка нет критических точек (то есть функция на нем сохраняет монотонность). Остается вычислить значение функции на концах отрезка: 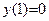 ,
, 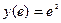 . Схема графика функции:
. Схема графика функции:
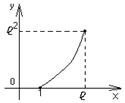 Ответ:
Ответ: 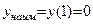 ,
, 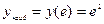 .
.
Пример 3. Найти наименьшее и наибольшее значения функции 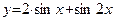 ,
, 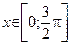 . Решение.
. Решение.
На данном замкнутом отрезке функция является непрерывной и имеет производную 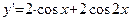
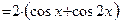 . Находим критические точки внутри заданного промежутка:
. Находим критические точки внутри заданного промежутка: 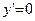 Þ
Þ 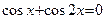 Û
Û 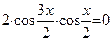 Û
Û
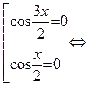
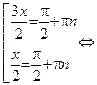
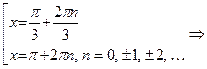 Þ только х1 =
Þ только х1 = 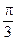 и х2 = p принадлежат
и х2 = p принадлежат 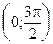 .
.
Вычисляем значения функции в критических точках и на концах промежутка:
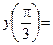
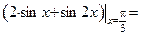
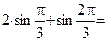
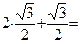
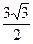 ;
; 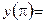
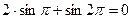 ;
;
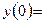
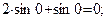
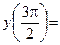
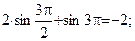 Схема графика функции:
Схема графика функции:
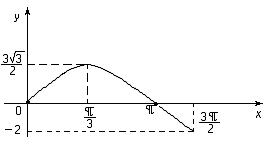 Ответ:
Ответ: 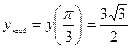 ,
, 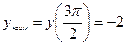 .
.
Во многих геометрических, физических и технических задачах требуется найти наибольшее и наименьшее значение величины, связанной функциональной зависимостью с другой величиной. Для решения такой задачи следует, исходя из её условия, выбрать независимую переменную и выразить исследуемую величину через эту переменную, а затем найти искомое наибольшее или наименьшее значение полученной функции. При этом промежуток изменения независимой переменной может быть конечным или бесконечным, он также определяется из условия задачи.
