Элементарные функции: линейная, квадратичная, дробно-линейная, обратная, степенная, показательная, логарифмическая, тригонометрические и обратные тригонометрические.
Операции над множествами
3.1 Объединением ( суммой) двух множеств 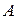 и
и 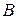 называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из данных множеств. Объединение записывается как
называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из данных множеств. Объединение записывается как
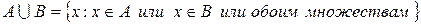 .
.
Пример.
Пусть 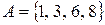 и
и 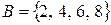 . Тогда объединение
. Тогда объединение 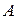 и
и 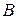 есть
есть 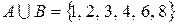 . При этом элементы 6 и 8 принадлежат обоим множествам.
. При этом элементы 6 и 8 принадлежат обоим множествам.
Аналогично определяется объединение более чем двух множеств. Объединение трех множеств 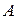 ,
, 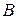 и
и 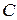 есть множество
есть множество 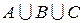 , каждый, из элементов которого принадлежит хотя бы одному из множеств
, каждый, из элементов которого принадлежит хотя бы одному из множеств 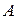 ,
, 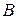 и
и 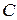 :
:
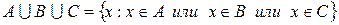 .
.
3.2 Пересечением (произведением) двух множеств 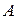 и
и 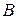 называется новое множество,состоящее из всех элементов, одновременно принадлежащих каждому из данных множеств
называется новое множество,состоящее из всех элементов, одновременно принадлежащих каждому из данных множеств 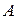 и
и 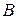 .
.
Пересечение записывается как 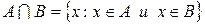 .
.
Пример . Пусть 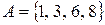 и
и 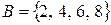 . Тогда
. Тогда 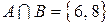 .
.
Пересечение более чем двух множеств определяется аналогичным образом. Пересечение трех множеств 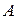 ,
, 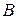 и
и 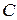 есть множество элементов, которые принадлежат
есть множество элементов, которые принадлежат 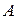 ,
, 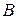 и
и 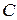 :
: 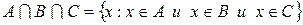 .
.
Если множества 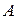 и
и 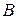 не имеют общих элементов, то их пересечение пусто:
не имеют общих элементов, то их пересечение пусто: 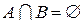 . Такие множества
. Такие множества 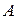 и
и 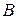 называются непересекающимися.
называются непересекающимися.
Пример. Пусть 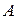 – множество целых положительных чисел, а
– множество целых положительных чисел, а 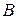 – множество целых отрицательных чисел. Тогда
– множество целых отрицательных чисел. Тогда 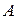 и
и 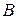 – непересекающиеся множества, так как не существует целых чисел, которые были бы одновременно и положительными, и отрицательными.
– непересекающиеся множества, так как не существует целых чисел, которые были бы одновременно и положительными, и отрицательными.
Определение непересекающихся множеств может быть распространено на случай более чем двух множеств.
Говорят, что 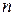 множеств
множеств 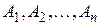 являются взаимно непересекающимися (или попарно непересекающимися), если никакие два из этих множеств не имеют общих элементов. Иными словами, множества
являются взаимно непересекающимися (или попарно непересекающимися), если никакие два из этих множеств не имеют общих элементов. Иными словами, множества 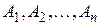 взаимно непересекающиеся, если
взаимно непересекающиеся, если 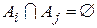 при
при 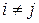 для
для 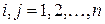 .
.
3.3 Разбиение множества на подмножества. В основе всевозможных классификаций, применяемых в биологии, лингвистике и других науках, лежит операция разбиения множества на попарно непересекающиеся подмножества. Одно и то же множество можно разбивать на подмножества разными способами: совокупность людей можно разделить на детей и взрослых, на мужчин и женщин
2. Ограниченные (сверху, снизу) и неограниченные (сверху, снизу) множества. Наибольший (наименьший) элемент множества.
Определение 1. Множество X 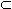 R называется ограниченным сверху, если существует такое число b
R называется ограниченным сверху, если существует такое число b 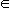 R, что для всех x
R, что для всех x 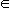 X имеет место неравенство x < b. Число b называется в этом случае числом, ограничивающим сверху множество X.
X имеет место неравенство x < b. Число b называется в этом случае числом, ограничивающим сверху множество X.
Множество X называется ограниченным снизу, если существует такое число a 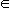 R, что для всех x
R, что для всех x 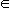 X выполняется неравенство x > a. Число a называется в этом случае числом, ограничивающим снизу множество X.
X выполняется неравенство x > a. Число a называется в этом случае числом, ограничивающим снизу множество X.
Множество, ограниченное сверху и снизу, называется ограниченным.
С помощью логических символов существования и всеобщности определение, например, ограниченного сверху множества можно записать следующим образом:
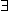 b b 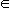 R R 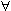 x x 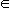 X: x < b X: x < b | (4.1) |
(здесь двоеточие означает "имеет место" или "выполняется условие").
Множество, не являющееся ограниченным сверху, называется неограниченным сверху.
Определение неограниченного сверху множества можно сформулировать и в позитивной форме, т. е. без отрицаний (без частицы "не"), следующим образом; множество X называется неограниченным сверху, если для любого числа b 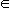 R найдется такой x
R найдется такой x 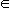 X, что x > b. Запишем это определение с помощью логических символов:
X, что x > b. Запишем это определение с помощью логических символов:
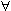 b b 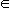 R R 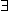 x x 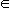 X: x > b X: x > b | (4.2) |
Сравнивая определения (4.1) и (4.2), видим, что при построении отрицания символ существования заменился на символ всеобщности, а символ всеобщности - на символ существования. Этим формальным правилом можно пользоваться при построении отрицаний в позитивной форме.
Аналогично, множество, не являющееся ограниченным снизу, называется неограниченным снизу.
Множество, не являющееся ограниченным, называется неограниченным.
Множество натуральных чисел N является примером ограниченного снизу множества. Если a 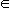 R и b
R и b 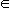 R, то отрезок [a, b] представляет собой ограниченное множество. Множества рациональных чисел Q, иррациональных чисел I, вообще всех чисел R дают примеры неограниченных множеств.
R, то отрезок [a, b] представляет собой ограниченное множество. Множества рациональных чисел Q, иррациональных чисел I, вообще всех чисел R дают примеры неограниченных множеств.
3. Понятие интервала, полуинтервала и отрезка. Абсолютная величина.

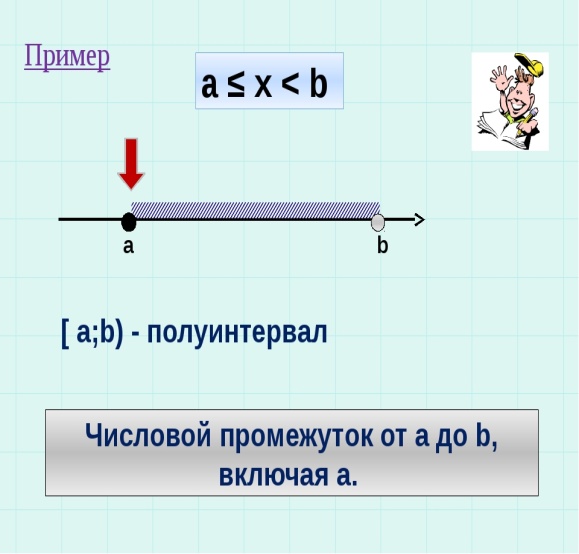
4. Понятие функции и способов ее задания. в тетр
Понятие функции является одним из основных понятий современной математики. С этим понятием часто встречаются при изучении реальных процессов в природе, науке и технике. С помощью различных функций могут быть описаны многие процессы и явления реального мира.
Определение.Отображения 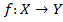 , где
, где 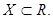 будем называть (вещественной) функцией действительного переменного.
будем называть (вещественной) функцией действительного переменного. 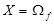 - область определения - совокупность всех значений независимой переменной х, для которых функция определена.
- область определения - совокупность всех значений независимой переменной х, для которых функция определена.
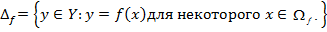 - множество значений f или образ f.
- множество значений f или образ f.
Определение. Если каждому элементу х множества X ( 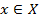 ) ставится в соответствие вполне определенный элемент у множества Y
) ставится в соответствие вполне определенный элемент у множества Y 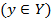 , то говорят, что на множестве X задана функция.
, то говорят, что на множестве X задана функция.
y = f(x), y = F(x) - функциональная зависимость х и у.
f, F - характеристики функции, х - независимая переменная (аргумент),
у - зависимая переменная.
Рассматривают три способа задания функции: аналитический, табличный и графический.
1. Аналитический.
Способ задания функции при помощи формулы называется аналитическим.Этот способ является основным в мат. анализе, но на практике не удобен.
2. Табличный способ задания функции.
Функцию можно задать с помощью таблицы, содержащей значения аргумента и соответствующие им значения функции.
3. Графический способ задания функции.
Функция у = f(х) называется заданной графически, если построен ее график. Такой способ задания функции дает возможность определять значения функции только приближенно, так как построение графика и нахождение на нем значений функции сопряжено с погрешностями
5. Свойства функций: четность, монотонность, ограниченность, периодичность. В тетр
Первый замечательный предел
Рассмотрим следующий предел: 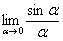 (вместо родной буквы «хэ» я буду использовать греческую букву «альфа», это удобнее с точки зрения подачи материала).
(вместо родной буквы «хэ» я буду использовать греческую букву «альфа», это удобнее с точки зрения подачи материала).
Согласно нашему правилу нахождения пределов пробуем подставить ноль в функцию: в числителе у нас получается ноль (синус нуля равен нулю), в знаменателе, очевидно, тоже ноль. Таким образом, мы сталкиваемся с неопределенностью вида 0/0 , которую, к счастью, раскрывать не нужно. В курсе математического анализа, доказывается, что:
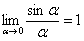
Данный математический факт носит название Первого замечательного предела. Нередко в практических заданиях функции могут быть расположены по-другому, это ничего не меняет:
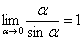 – тот же самый первый замечательный предел.
– тот же самый первый замечательный предел.
! Но самостоятельно переставлять числитель и знаменатель нельзя! Если дан предел в виде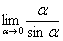 , то и решать его нужно в таком же виде, ничего не переставляя.
, то и решать его нужно в таком же виде, ничего не переставляя.
На практике в качестве параметра 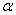 может выступать не только переменная
может выступать не только переменная 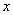 , но и элементарная функция, сложная функция. Важно лишь, чтобы она стремилась к нулю.
, но и элементарная функция, сложная функция. Важно лишь, чтобы она стремилась к нулю.
Примеры:
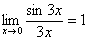 ,
, 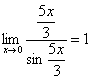 ,
, 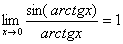 ,
, 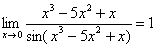
Здесь 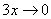 ,
, 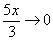 ,
, 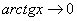 ,
, 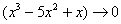 , и всё гуд – первый замечательный предел применим.
, и всё гуд – первый замечательный предел применим.
А вот следующая запись – ересь:
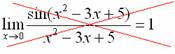
Почему? Потому что многочлен 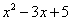 не стремится к нулю, он стремится к пятерке.
не стремится к нулю, он стремится к пятерке.
Кстати, вопрос на засыпку, а чему равен предел 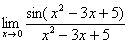 ? Ответ можно найти.
? Ответ можно найти.
Переходим к рассмотрению практических примеров:
Пример 1
Найти предел 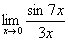
Если мы замечаем в пределе синус, то это нас сразу должно наталкивать на мысль о возможности применения первого замечательного предела.
Сначала пробуем подставить 0 в выражение под знак предела (делаем это мысленно или на черновике):
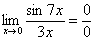 Итак, у нас есть неопределенность вида
Итак, у нас есть неопределенность вида 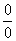 , ее обязательно указываем в оформлении решения. Выражение под знаком предела у нас похоже на первый замечательный предел, но это не совсем он, под синусом находится
, ее обязательно указываем в оформлении решения. Выражение под знаком предела у нас похоже на первый замечательный предел, но это не совсем он, под синусом находится 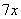 , а в знаменателе
, а в знаменателе 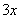 .
.
В подобных случаях первый замечательный предел нам нужно организовать самостоятельно, используя искусственный прием. Ход рассуждений может быть таким: «под синусом у нас 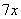 , значит, в знаменателе нам тоже нужно получить
, значит, в знаменателе нам тоже нужно получить 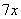 ».
».
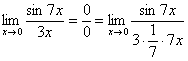
То есть, знаменатель искусственно умножается в данном случае на 7 и делится на ту же семерку. Теперь запись у нас приняла знакомые очертания.
Когда задание оформляется от руки, то первый замечательный предел желательно пометить простым карандашом:
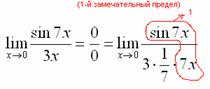
Что произошло? По сути, обведенное выражение у нас превратилось в единицу и исчезло в произведении:
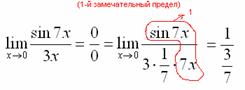
Теперь только осталось избавиться от трехэтажности дроби:
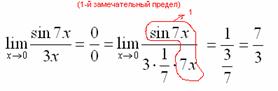 Готово. Окончательный ответ:
Готово. Окончательный ответ: 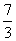
Если не хочется использовать пометки карандашом, то решение можно оформить так:
“
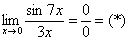
Используем первый замечательный предел 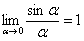
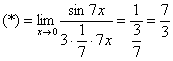
“
Пример 2
Найти предел 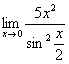
Опять мы видим в пределе дробь и синус. Пробуем подставить в числитель и знаменатель ноль:
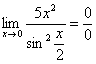 Действительно, у нас неопределенность
Действительно, у нас неопределенность 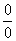 и, значит, нужно попытаться организовать первый замечательный предел. что когда у нас есть неопределенность
и, значит, нужно попытаться организовать первый замечательный предел. что когда у нас есть неопределенность 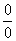 , то нужно разложить числитель и знаменатель на множители. Здесь – то же самое, степени мы представим в виде произведения (множителей):
, то нужно разложить числитель и знаменатель на множители. Здесь – то же самое, степени мы представим в виде произведения (множителей):
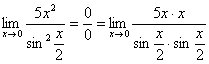
Далее, по уже знакомой схеме организовываем первые замечательные пределы. Под синусами у нас 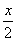 , значит, в числителе тоже нужно получить
, значит, в числителе тоже нужно получить 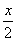 :
:
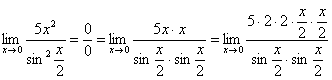
Аналогично предыдущему примеру, обводим карандашом замечательные пределы (здесь их два), и указываем, что они стремятся к единице:
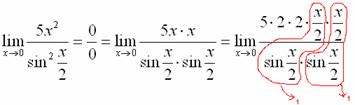
Собственно, ответ готов:
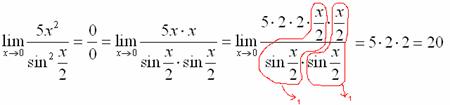
В следующих примерах, я не буду заниматься художествами в Пэйнте, думаю, как правильно оформлять решение в тетради – Вам уже понятно.
Пример 3
Найти предел 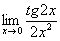
Подставляем ноль в выражение под знаком предела:
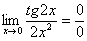
Получена неопределенность 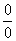 , которую нужно раскрывать. Если в пределе есть тангенс, то почти всегда его превращают в синус и косинус по известной тригонометрической формуле
, которую нужно раскрывать. Если в пределе есть тангенс, то почти всегда его превращают в синус и косинус по известной тригонометрической формуле 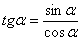 (кстати, с котангенсом делают примерно то же самое, см. методический материал ). В данном случае:
(кстати, с котангенсом делают примерно то же самое, см. методический материал ). В данном случае:
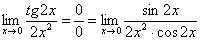 Косинус нуля равен единице, и от него легко избавиться (не забываем пометить, что он стремится к единице):
Косинус нуля равен единице, и от него легко избавиться (не забываем пометить, что он стремится к единице):
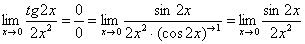 Таким образом, если в пределе косинус является МНОЖИТЕЛЕМ, то его, грубо говоря, нужно превратить в единицу, которая исчезает в произведении.
Таким образом, если в пределе косинус является МНОЖИТЕЛЕМ, то его, грубо говоря, нужно превратить в единицу, которая исчезает в произведении.
Дальше по накатанной схеме, организуем первый замечательный предел:
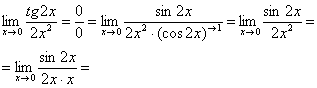
Здесь все вышло проще, без всяких домножений и делений. Первый замечательный предел тоже превращается в единицу и исчезает в произведении:
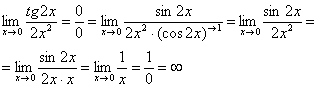
В итоге получена бесконечность, бывает и такое.
Пример 4
Найти предел 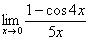 Пробуем подставить ноль в числитель и знаменатель:
Пробуем подставить ноль в числитель и знаменатель:
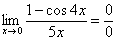
Получена неопределенность 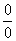 (косинус нуля, как мы помним, равен единице)
(косинус нуля, как мы помним, равен единице)
Используем тригонометрическую формулу 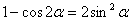 . Возьмите на заметку! Пределы с применением этой формулы почему-то встречаются очень часто.
. Возьмите на заметку! Пределы с применением этой формулы почему-то встречаются очень часто.
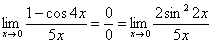 Постоянные множители вынесем за значок предела:
Постоянные множители вынесем за значок предела:
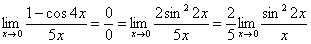 Организуем первый замечательный предел:
Организуем первый замечательный предел:
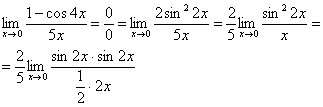
Здесь у нас только один замечательный предел, который превращается в единицу и исчезает в произведении:
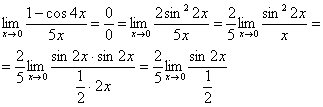 Избавимся от трехэтажности:
Избавимся от трехэтажности:
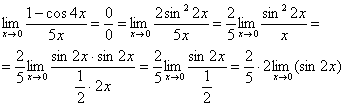
Предел фактически решен, указываем, что оставшийся синус стремится к нулю:
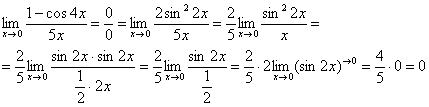
Пример 5
Найти предел 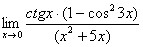 Этот пример сложнее, попробуйте разобраться самостоятельно:
Этот пример сложнее, попробуйте разобраться самостоятельно:
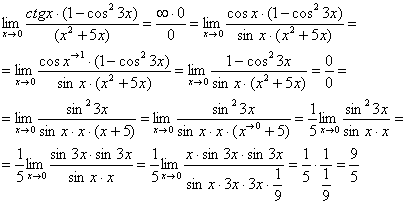
Некоторые пределы можно свести к 1-му замечательному пределу путём замены переменно
Второй замечательный предел
В теории математического анализа доказано, что:
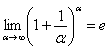
Данный факт носит название второго замечательного предела.
Справка: 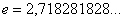 – это иррациональное число.
– это иррациональное число.
В качестве параметра 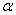 может выступать не только переменная
может выступать не только переменная 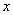 , но и сложная функция. Важно лишь, чтобы она стремилась к бесконечности.
, но и сложная функция. Важно лишь, чтобы она стремилась к бесконечности.
Пример 6 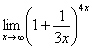 Найти предел
Найти предел
Когда выражение под знаком предела находится в степени – это первый признак того, что нужно попытаться применить второй замечательный предел.Но сначала, как всегда, пробуем подставить бесконечно большое число в выражение 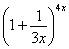 Нетрудно заметить, что при
Нетрудно заметить, что при  основание степени
основание степени 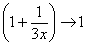 , а показатель –
, а показатель – 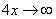 , то есть имеется, неопределенность вида
, то есть имеется, неопределенность вида 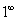 :
:
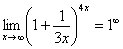 Данная неопределенность как раз и раскрывается с помощью второго замечательного предела. Но, как часто бывает, второй замечательный предел не лежит на блюдечке с голубой каемочкой, и его нужно искусственно организовать. Рассуждать можно следующим образом: в данном примере параметр
Данная неопределенность как раз и раскрывается с помощью второго замечательного предела. Но, как часто бывает, второй замечательный предел не лежит на блюдечке с голубой каемочкой, и его нужно искусственно организовать. Рассуждать можно следующим образом: в данном примере параметр 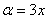 , значит, в показателе нам тоже нужно организовать
, значит, в показателе нам тоже нужно организовать 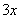 . Для этого возводим основание в степень
. Для этого возводим основание в степень 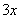 , и, чтобы выражение не изменилось – возводим в степень
, и, чтобы выражение не изменилось – возводим в степень 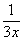 :
:
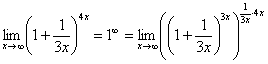
Когда задание оформляется от руки, карандашом помечаем:
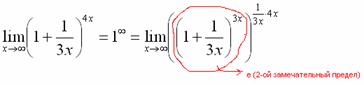
Практически всё готово, страшная степень превратилась в симпатичную букву 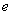 :
:
При этом сам значок предела перемещаем в показатель:
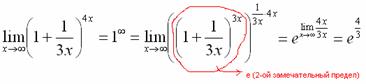
Далее, отметки карандашом я не делаю, принцип оформления, думаю, понятен.
Пример 7
Найти предел 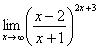
Внимание! Предел подобного типа встречается очень часто, пожалуйста, очень внимательно изучите данный пример.
Пробуем подставить бесконечно большое число в выражение, стоящее под знаком предела:
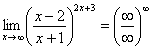
В результате получена неопределенность 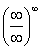 . Но второй замечательный предел применим к неопределенности вида
. Но второй замечательный предел применим к неопределенности вида 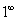 . Что делать? Нужно преобразовать основание степени. Рассуждаем так: в знаменателе у нас
. Что делать? Нужно преобразовать основание степени. Рассуждаем так: в знаменателе у нас 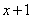 , значит, в числителе тоже нужно организовать
, значит, в числителе тоже нужно организовать 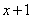 :
:
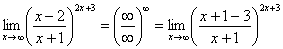
Теперь можно почленно разделить числитель на знаменатель:
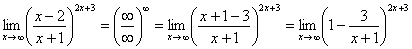
Вроде бы основание стало напоминать 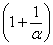 , но у нас знак «минус» да и тройка какая-то вместо единицы. Поможет следующее ухищрение, делаем дробь трехэтажной:
, но у нас знак «минус» да и тройка какая-то вместо единицы. Поможет следующее ухищрение, делаем дробь трехэтажной:
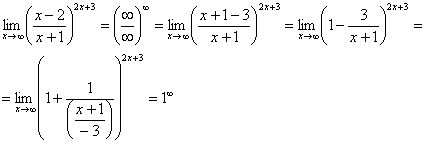
Таким образом, основание приняло вид 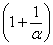 , и, более того, появилась нужная нам неопределенность
, и, более того, появилась нужная нам неопределенность 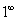 . Организуем второй замечательный предел
. Организуем второй замечательный предел 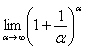 .
.
Легко заметить, что в данном примере 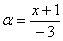 . Снова исполняем наш искусственный прием: возводим основание степени в
. Снова исполняем наш искусственный прием: возводим основание степени в 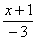 , и, чтобы выражение не изменилось – возводим в обратную дробь
, и, чтобы выражение не изменилось – возводим в обратную дробь 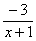 :
:
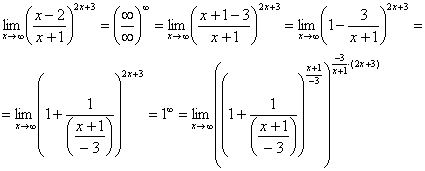
Наконец-то долгожданное 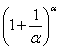 устроено, с чистой совестью превращаем его в букву
устроено, с чистой совестью превращаем его в букву 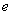 :
:
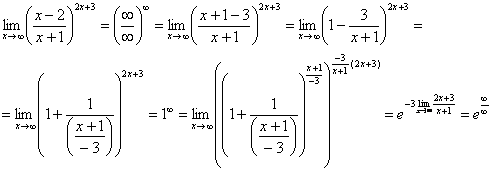
Но на этом мучения не закончены, в показателе у нас появилась неопределенность вида 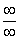 , Делим числитель и знаменатель на
, Делим числитель и знаменатель на 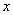 :
:

Готово.
А сейчас мы рассмотрим модификацию второго замечательного предела. Напомню, что второй замечательный предел выглядит следующим образом: 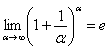 . Однако на практике время от времени можно встретить его «перевёртыш», который в общем виде записывается так:
. Однако на практике время от времени можно встретить его «перевёртыш», который в общем виде записывается так:
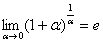
Пример 8
Найти предел 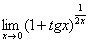
Сначала (мысленно или на черновике) пробуем подставить ноль (бесконечно малое число) в выражение, стоящее под знаком предела:
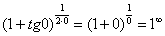
В результате получена знакомая неопределенность 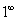 . Очевидно, что в данном примере
. Очевидно, что в данном примере 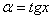 . С помощью знакомого искусственного приема организуем в показателе степени конструкцию
. С помощью знакомого искусственного приема организуем в показателе степени конструкцию 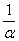 :
:
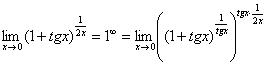
Выражение 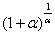 со спокойной душой превращаем в букву
со спокойной душой превращаем в букву 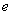 :
:
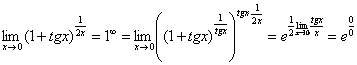
Еще не всё, в показателе у нас появилась неопределенность вида 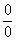 . Раскладываем тангенс на синус и косинус (ничего не напоминает?):
. Раскладываем тангенс на синус и косинус (ничего не напоминает?):
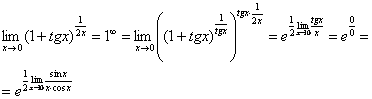
Косинус нуля стремится к единице (не забываем помечать карандашом), поэтому он просто пропадает в произведении:

Пример 14.
Найти производную функции 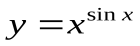 .
.
Решение.
Прологарифмируем обе части функции и преобразуем выражение:
 .
.
Теперь дифференцируем уравнение, как неявно заданную функцию:
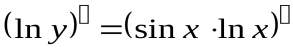 ;
;
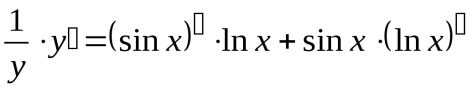 ;
;
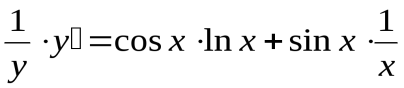 ;
;
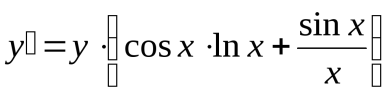 ;
;
Так как 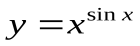 , то окончательно получаем:
, то окончательно получаем:
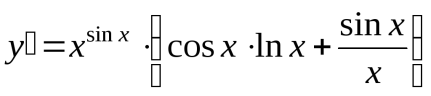
26. Производные неявных функций. Что такое неявная функция? Давайте сначала вспомним: Функция одной переменной 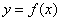 –это правило, по которому каждому значению независимой переменной
–это правило, по которому каждому значению независимой переменной 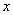 соответствует одно и только одно значение функции
соответствует одно и только одно значение функции 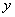 .
.
Переменная 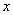 называется независимой переменной или аргументом.
называется независимой переменной или аргументом.
Переменная 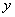 называется зависимой переменной или функцией.
называется зависимой переменной или функцией.
До сих пор мы рассматривали функции, заданные в явном виде. Что это значит? Устроим разбор полётов на конкретных примерах.
Рассмотрим функцию 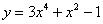
Мы видим, что слева у нас одинокий «игрек», а справа – только «иксы». То есть, функция 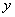 в явном виде выражена через независимую переменную
в явном виде выражена через независимую переменную 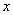 .
.
Рассмотрим другую функцию: 
Здесь переменные 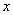 и
и 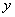 расположены «вперемешку». Причем никакими способами невозможно выразить «игрек» только через «икс». Что это за способы? Перенос слагаемых из части в часть со сменой знака, вынесение за скобки, перекидывание множителей по правилу пропорции и др. Перепишите равенство
расположены «вперемешку». Причем никакими способами невозможно выразить «игрек» только через «икс». Что это за способы? Перенос слагаемых из части в часть со сменой знака, вынесение за скобки, перекидывание множителей по правилу пропорции и др. Перепишите равенство  и попробуйте выразить «игрек» в явном виде:
и попробуйте выразить «игрек» в явном виде: 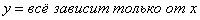 . Можно крутить-вертеть уравнение часами, но у вас этого не получится.:
. Можно крутить-вертеть уравнение часами, но у вас этого не получится.:  – пример неявной функции.
– пример неявной функции.
В курсе математического анализа доказано, что неявная функция существует (однако не всегда), у неё есть график (точно так же, как и у «нормальной» функции). У неявной функции точно так же существует первая производная, вторая производная и т.д. Как говорится, все права секс-меньшинств соблюдены.
.Пример 1 Найти производную от функции, заданной неявно 
1) На первом этапе навешиваем штрихи на обе части:
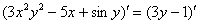
2) Используем правила линейности производной 
3) Непосредственное дифференцирование.
Как дифференцировать 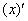 и
и 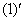 совершенно понятно. Что делать там, где под штрихами есть «игреки»?
совершенно понятно. Что делать там, где под штрихами есть «игреки»?
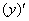 – просто до безобразия, производная от функции равна её производной:
– просто до безобразия, производная от функции равна её производной: 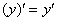 .
.
Как дифференцировать 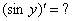
Здесь у нас сложная функция. Почему? Вроде бы под синусом всего одна буква «игрек». Но, дело в том, что всего одна буква «игрек» – САМА ПО СЕБЕ ЯВЛЯЕТСЯ ФУНКЦИЕЙ(см. определение в начале урока). Таким образом, синус – внешняя функция, 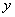 – внутренняя функция. Используем правило дифференцирования сложной функции
– внутренняя функция. Используем правило дифференцирования сложной функции 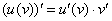 :
:
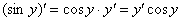 Произведение дифференцируем по обычному правилу
Произведение дифференцируем по обычному правилу 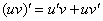 :
:
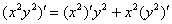
Обратите внимание, что  – тоже сложная функция, любой «игрек с наворотами» – сложная функция:
– тоже сложная функция, любой «игрек с наворотами» – сложная функция:
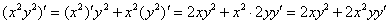
Само оформление решения должно выглядеть примерно так:
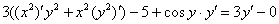
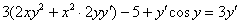
Если есть скобки, то раскрываем их: 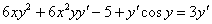
4) В левой части собираем слагаемые, в которых есть «игрек» со штрихом. В правую часть – переносим всё остальное:
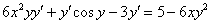 5) В левой части выносим производную
5) В левой части выносим производную 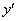 за скобки:
за скобки:
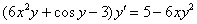 6) И по правилу пропорции сбрасываем эти скобки в знаменатель правой части:
6) И по правилу пропорции сбрасываем эти скобки в знаменатель правой части:
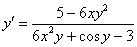 Производная найдена. Готово.
Производная найдена. Готово.
Интересно отметить, что в неявном виде можно переписать любую функцию. Например, функцию 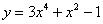 можно переписать так:
можно переписать так: 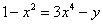 . И дифференцировать её по только что рассмотренному алгоритму. На самом деле фразы «функция, заданная в неявном виде» и «неявная функция» отличаются одним смысловым нюансом. Фраза «функция, заданная в неявном виде» более общая и корректная,
. И дифференцировать её по только что рассмотренному алгоритму. На самом деле фразы «функция, заданная в неявном виде» и «неявная функция» отличаются одним смысловым нюансом. Фраза «функция, заданная в неявном виде» более общая и корректная, 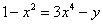 – эта функция задана в неявном виде, но здесь можно выразить «игрек» и представить функцию в явном виде. Под фразой «неявная функция» понимают «классическую» неявную функцию, когда «игрек» выразить нельзя.
– эта функция задана в неявном виде, но здесь можно выразить «игрек» и представить функцию в явном виде. Под фразой «неявная функция» понимают «классическую» неявную функцию, когда «игрек» выразить нельзя.
Второй способ решения
Внимание! Со вторым способом можно ознакомиться только в том случае, если Вы умеете уверенно находить частные производные. Начинающие изучать математический анализ и чайники, пожалуйста, не читайте и пропустите этот пункт, иначе в голове будет полная каша.
Найдем производную неявной функции  вторым способом.
вторым способом.
Переносим все слагаемые в левую часть: 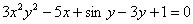
И рассматриваем функцию двух переменных: 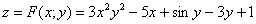
Тогда нашу производную можно найти по формуле 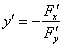
Найдем частные производные:
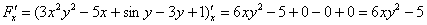
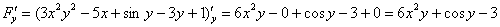
Таким образом:
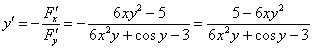
Второй способ решения позволяет выполнить проверку. Но оформлять им чистовой вариант задания нежелательно, поскольку частные производные осваивают позже, и студент, изучающий тему «Производная функции одной переменной», знать частные производные как бы еще не должен.
Рассмотрим еще несколько примеров.
Пример 2
Найти производную от функции, заданной неявно 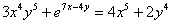
Навешиваем штрихи на обе части:
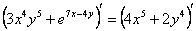
Используем правила линейности:
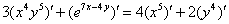
Находим производные:
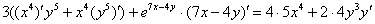
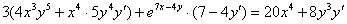
Раскрываем все скобки:
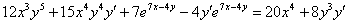
Переносим все слагаемые с 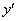 в левую часть, остальные – в правую часть:
в левую часть, остальные – в правую часть:
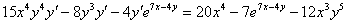
У В левой части выносим 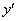 за скобку:
за скобку:
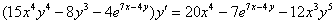
Окончательный ответ:

Пример 4
Найти производную от функции, заданной неявно 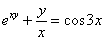
Заключаем обе части под штрихи и используем правило линейности:
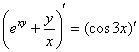
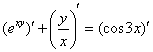
Дифференцируем, используя правило дифференцирования сложной функции 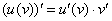 и правило дифференцирования частного
и правило дифференцирования частного 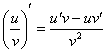 :
:
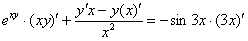

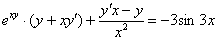
Раскрываем скобки:
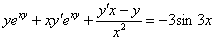
Теперь нам нужно избавиться от дроби. Это можно сделать и позже, но рациональнее сделать сразу же. В знаменателе дроби находится 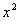 . Умножаем каждое слагаемое каждой части на
. Умножаем каждое слагаемое каждой части на 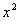 . Если подробно, то выглядеть это будет так:
. Если подробно, то выглядеть это будет так:
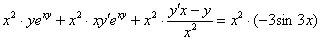
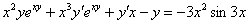
Иногда после дифференцирования появляется 2-3 дроби. Если бы у нас была еще одна дробь, например, 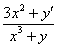 , то операцию нужно было бы повторить – умножить каждое слагаемое каждой части на
, то операцию нужно было бы повторить – умножить каждое слагаемое каждой части на 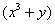
Далее алгоритм работает стандартно, после того, как все скобки раскрыты, все дроби устранены, слагаемые, где есть «игрек штрих» собираем в левой части, а в правую часть переносим всё остальное:
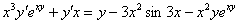
В левой части выносим 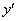 за скобку:
за скобку:
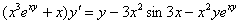
Окончательный ответ:
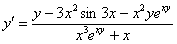
27. Параметрически заданные функции и их дифференцирование.
Правило Лопиталя.
Первое правило Лопиталя
Пусть функции f (x) и g (x) непрерывны на отрезке [а, b] и дифференцируемы на интервале (а, b), и пусть g ' (x) ≠ 0 всюду в (а, b). Пусть, далее, известно, что f (а) = g (а) = 0. Тогда говорят, что отношение 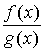 при х → а + 0 представляет собой неопределённость вида 0/0.Теорема. Если при указанных условиях
при х → а + 0 представляет собой неопределённость вида 0/0.Теорема. Если при указанных условиях
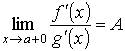 , то и
, то и 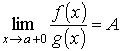 . Доказательство. Предположим, что ∞ < A < + ∞. Для заданного как угодно малого числа e > 0 выберем х0 так, чтобы в интервале (а, x0) выполнялось неравенство
. Доказательство. Предположим, что ∞ < A < + ∞. Для заданного как угодно малого числа e > 0 выберем х0 так, чтобы в интервале (а, x0) выполнялось неравенство 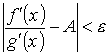 .
.
Применим теорему Коши к отрезку [а, x0], Если х  [а, x0], то существует такая точка с
[а, x0], то существует такая точка с  [а, x], что
[а, x], что
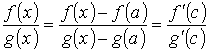 и, следовательно, для всех х
и, следовательно, для всех х  [а, x0] справедливо неравенство
[а, x0] справедливо неравенство
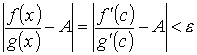 . Это означает, что
. Это означает, что 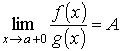 . Второе правило Лопиталя Пусть функции f (x) и g (x) непрерывны и дифференцируемы в интервале (a, b) (может быть, бесконечном) и g' (x) не обращается в нуль в (a, b). Пусть известно, что
. Второе правило Лопиталя Пусть функции f (x) и g (x) непрерывны и дифференцируемы в интервале (a, b) (может быть, бесконечном) и g' (x) не обращается в нуль в (a, b). Пусть известно, что 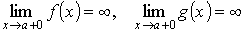 . Тогда говорят, что отношение
. Тогда говорят, что отношение 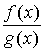 прих → а + 0 представляет собой неопределённость вида
прих → а + 0 представляет собой неопределённость вида
