Вопрос 8. Свойства пределов. Односторонние пределы. Бесконечно малые и большие величины.

Свойство 1. Постоянный множитель c можно выносить за знак предела:

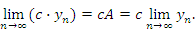
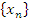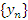Свойство 2. Если существуют конечные пределы последовательностей и , то

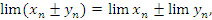
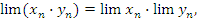
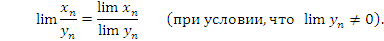
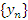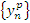Свойство 3. Если существуют конечные пределы последовательностей и , то

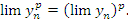
Интуитивные соображения. Пусть 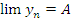. Тогда 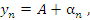где 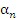– некоторая бесконечно малая величина. Следовательно,

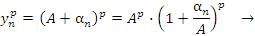
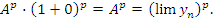
Последовательность 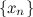называется бесконечно малой последовательностью (б.м.п.), если для любого 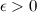существует номер 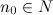такой, что для любого 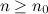выполняется неравенство: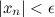

Последовательность 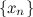называется бесконечно большой (б.б.п.), если для любого 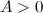существует номер 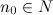такой, что для любого 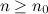выполняется неравенство: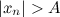

Если f(x) стремится к пределу b при x стремящемся к некоторому числу a так, что xпринимает только значения, меньшие a, то пишут 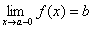и называют bпределом функции f(x) в точке a слева.

Таким образом, число b называется пределом функции y=f(x) при x→aслева, если каково бы ни было положительное число ε, найдется такое число δ (меньшее a), что для всех 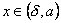выполняется неравенство .

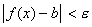Аналогично, если x→a и принимает значения большие a, то пишут 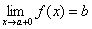и называют b пределом функции в точке а справа. Т.е. число b называется пределом функции y=f(x) при x→aсправа, если каково бы ни было положительное число ε, найдется такое число δ (большее а), что для всех 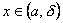выполняется неравенство .

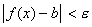Основные свойства б.м. и б.б. последовательностей

1° Сумма б.м. последовательностей есть б.м.п.

2° Произведение ограниченной последовательности и б.м. есть б.м.п.

3° Если 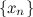- б.м.п., то 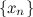- ограниченная последовательность.

4° Произведение б.м.п. есть последовательность б.м.

5° Если 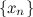- б.м.п. и 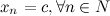, то 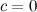, т.е.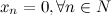

6° Если 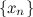- б.м.п. и 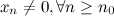, то последовательность 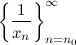- б.б.п.

7° Если 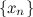- б.б.п., то 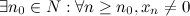и последовательность 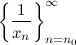- б.м.п.

Вопрос 9. Эквивалентные функции. Предел отношения бесконечно малых (больших) функций.

Б.м. функци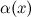и и 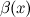называются эквивалентными или равносильными б.м. одного порядка при 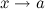, если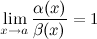

Обозначают: 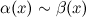при .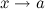

Пример

Задание. Проверить, являются ли функци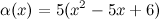и и 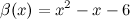эквивалентными бесконечно малыми при .

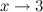Решение. Проверим вначале, что данные функции являютсябесконечно малыми функциями в точке :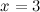

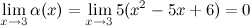
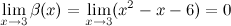
Найдем предел отношения этих функций:

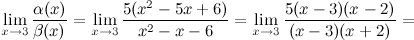
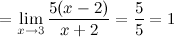
Ответ. Заданные функци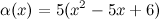и и 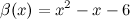являются эквивалентными бесконечно малыми.

Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.

.

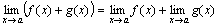Доказательство. Проведем доказательство для двух слагаемых, так как для любого числа слагаемых оно проводится так же. Пусть 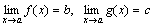.Тогда f(x)=b+α(x)и g(x)=c+β(x), где α и β – бесконечно малые функции. Следовательно,

f(x) + g(x)=(b + c) + (α(x) + β(x)).

Так как b + cесть постоянная величина, а α(x) + β(x) – функция бесконечно малая, то

.

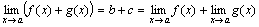Пример. .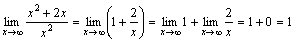

Теорема 2. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:

.

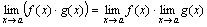Доказательство. Пусть 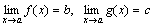. Следовательно, f(x)=b+α(x) иg(x)=c+β(x) и

fg = (b + α)(c + β) = bc + (bβ + cα + αβ).

Произведение bc есть величина постоянная. Функция bβ + c α + αβ на основании свойств бесконечно малых функций есть величина бесконечно малая. Поэтому .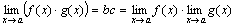

Следствие 1. Постоянный множитель можно выносить за знак предела:

.

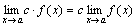Следствие 2. Предел степени равен степени предела:

.

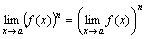Пример. .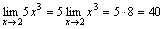

Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е.

.

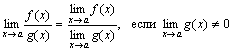Доказательство. Пусть 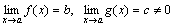. Следовательно, f(x)=b+α(x) и g(x)=c+β(x), где α, β – бесконечно малые. Рассмотрим частное

.

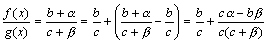Дробь 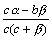является бесконечно малой функцией, так как числитель есть бесконечно малая функция, а знаменатель имеет предел c²≠0.

Примеры.

1. .
2. .
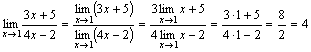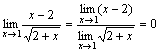3. Рассмотрим 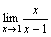. При x→1 числитель дроби стремится к 1, а знаменатель стремится к 0. Но так как 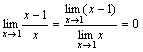, т.е. 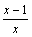есть бесконечно малая функция при x→1, то .

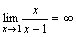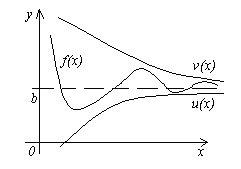Теорема 4. Пусть даны три функции f(x), u(x) иv(x), удовлетворяющие неравенствам u(x)≤f(x)≤ v(x). Если функции u(x) и v(x) имеют один и тот же предел при x→a (или x→∞), то и функция f(x)стремится к тому же пределу, т.е. если

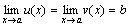, то .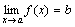

Смысл этой теоремы понятен из рисунка.

Теорема 5. Если при x→a (или x→∞) функция y=f(x) принимает неотрицательные значения y≥0 и при этом стремится к пределу b, то этот предел не может быть отрицательным: b≥0.

Доказательство. Доказательство проведем методом от противного. Предположим, что b<0, тогда |y – b|≥|b| и, следовательно, модуль разности не стремится к нулю при x→a. Но тогда y не стремится к пределу b при x→a, что противоречит условию теоремы.

Теорема 6. Если две функции f(x) и g(x) при всех значениях аргумента xудовлетворяют неравенству f(x)≥ g(x) и имеют пределы 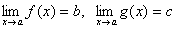, то имеет место неравенство b≥c.

Доказательство. По условию теоремы f(x)-g(x) ≥0, следовательно, по теореме 5 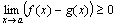, или 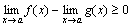.