Первообразная функции и неопределенный интеграл.

Функция F(x), определенная на некотором промежутке действительной оси, называется первообразной для действительной функции f(x), определенной на том же промежутке, если F'(x) = f(x) для всех х из этого промежутка.

Достаточное условие существования первообразной у заданной функции f – непрерывность этой функции.

У заданной на промежутке функции f любые две первообразные отличаются на постоянную,

т.е. если F'1(x) = f(x) и F'2(x) = f(x),

то F1(x) – F2(x) =C = const для всех х из промежутка определения функции f.

Неопределенный интеграл: от заданной на некотором промежутке действительной оси действительной функции f(x) определяется как множество всех ее первообразных на этом промежутке и обозначается

Свойства неопределенного интеграла.

Понятие определенного интеграла. Свойства и геометрическая интерпретация определенного интеграла.

Теорема 1.Определённый интеграл с одинаковыми пределами интегрирования равен нулю, т.е.

Это свойство содержится в самом определении определённого интеграла. Однако его можно получить и по формуле Ньютона-Лейбница:

Теорема 2.Величина определённого интеграла не зависит от обозначения переменной интегрирования, т.е.

Пусть F(x) – первообразная для f(x). Для f(t) первообразной служит та же функцияF(t), в которой лишь иначе обозначена независимая переменная. Следовательно,

На основании формулы последнее равенство означает равенство интегралов

и

Теорема 3.Постоянный множитель можно выносить за знак определённого интеграла, т.е.

Теорема 4.Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций, т.е.

Теорема 5.Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям, т.е. если

то

Теорема 6.При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак, т.е.

Теорема 7(теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке внутри его, т.е.

Теорема 8.Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если

Теорема 9.Если верхний предел интегрирования больше нижнего и функции и непрерывны, то неравенство

можно почленно интегрировать, т.е.

Формула Ньютона-Лейбница.

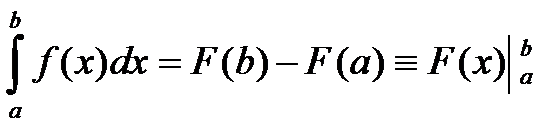
Основные понятия теории вероятностей. Пространство элементарных событий.

Теория вероятностей - математическая наука, изучающая количественные закономерности массовых случайных явлений.

Под случайными явлениями (или событиями) понимаются явления с неопределенным исходом, происходящие при неоднократном воспроизведении некоторого комплекса условий

Опыт – физический процесс, существующий или созданный, протекающий при некотором комплексе условий

Комплекс условий и есть испытание, опыт, а всякое событие есть исход этого испытания

Событие – факт, который может произойти или не произойти в результате опыта

События:

· достоверные

· обязательно должно произойти в результате испытания

· невозможные

· не может произойти в результате испытания

· случайные

· может произойти или не произойти

· несовместные

· появление одного из них в единичном испытании исключает появление другого в этом же испытании

· совместные

· в противном случае.

· единственно возможные

· если в результате испытания должно произойти хотя бы одно из них

· противоположные

· два единственно возможных и несовместных события

· независимые

· появление одного события не зависит от появления или не появления другого

· зависимые

· появление одного события зависит от появления или не появления другого

· равновозможные

· в результате испытания ни одно из этих событий не является объективно более возможным

· полная группа

· единственно возможные и несовместные

· элементарные

· образуют полную группу и равновозможные