Первообразная и неопределённый интеграл

Лекция 5. Первообразная и неопределённый интеграл. Свойства неопределённого интеграла. Таблица первообразных. Простейшие приёмы интегрирования: подведение функции под знак дифференциала, выделение полного квадрата, замена переменных и интегрирование по частям в неопределённом интеграле. Определённый интеграл, его свойства и геометрический смысл

Операция, обратная дифференцированию, называется интегрированием. Перейдём к её изложению.

Первообразная и неопределённый интеграл

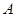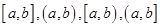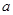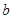Ниже в качестве берётся любой из промежутков: (концы и могут быть бесконечными).

Определение 1.Говорят, что функция 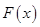является первообразной для функции 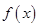на множестве 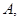если 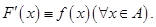Разыскание всех первообразных функции 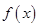называется интегрированием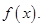

Например, функция 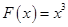является первообразной для 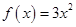на всей оси 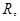так как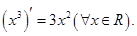

Теорема 1(об общем виде всех первообразных данной функции).Пусть 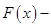фиксированная первообразная функции 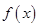(на множестве 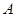). Тогда множество всех первообразных функции 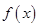(на множестве 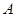) описывается формулой

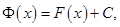
где 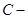произвольная постоянная.

Доказательствовытекает из того, что есл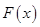и и 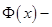две первообразные функции 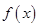, то 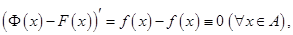а, значит, разность 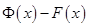является постоянной величиной на множестве 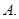, т.е.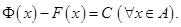

Определение 2.Совокупность всех первообразных функции 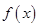(на множестве 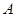) называется неопределённым интегралом на 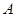этой функции. Обозначение: 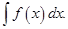При этом сама функция 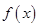называется подынтегральной функцией и если интеграл от неё существует, то говорят, что 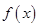интегрируема на .

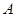Из теоремы 1 вытекает, что 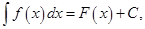где 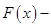фиксированная первообразная функции 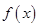(на множестве 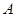), а 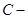произвольная постоянная. Отметим, что равенство 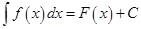равносильно равенству 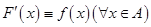. Таким образом, для доказательства того, что некоторая функция 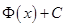является неопределённым интегралом от функции 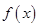надо продифференцировать её по 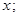если при этом будет получена подынтегральная функция 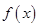, то равенство 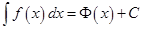будет истинным. Используя этот факт, легко докажем следующие формулы.

Таблица неопределённых интегралов (ниже везде 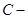произвольная постоянная)

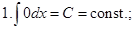
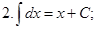
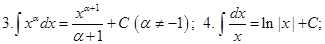
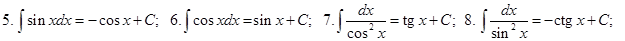
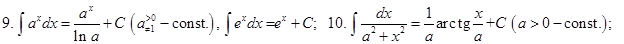
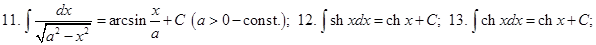
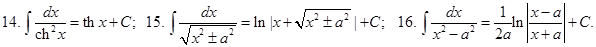
Докажем, например, формулу 10. Дифференцируем правую часть равенства 10 по :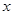

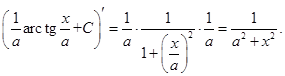
Получена подынтегральная функция левой части 10. Значит, равенство 10 верно. Точно так же доказываются остальные формулы этой таблицы.

Свойства неопределённого интеграла (везде ниже предполагается, что интегралы от соответствующих функций существуют):

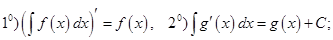
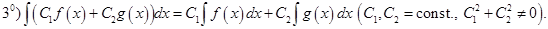
Свойство 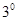называют свойством линейности интеграла. Первые два свойства показывают, что операции дифференцирования и интегрирования взаимно обратны.

Немного позже будет установлено, что всякая непрерывная на промежутке 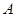функция 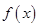интегрируема на этом промежутке.