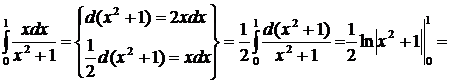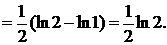Интегрирование путем подведения под знак дифференциала и методом подстановки

При сведении интеграла к табличному часто используют метод интегрирования путем подведения под знак дифференциала. В данном случае используют следующую формулу:

,

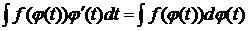где 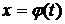– функция, имеющая непрерывную производную на рассматриваемом промежутке.

Применяют также интегрирование методом подстановки.

Обозначим 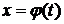, тогда получим 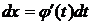. Тогда

.

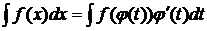Подведение под знак дифференциала есть одна из реализаций метода замены переменной.

Удачная замена переменной позволяет упростить исходный интеграл, а иногда свести его даже к табличному.

Примеры.Вычислить следующие интегралы:

1. .

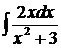1 способ.

.

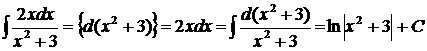2 способ.

.

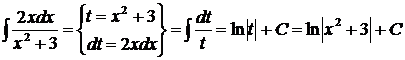2. .

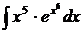1 способ.

.

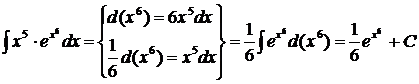2 способ.

.

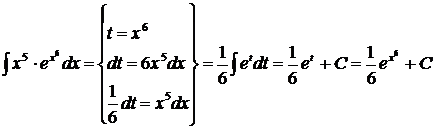3. .

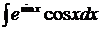1 способ.

.

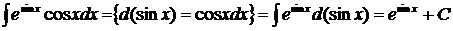2. способ.

.

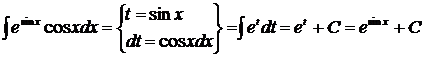
4. .

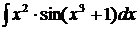1 способ.

.

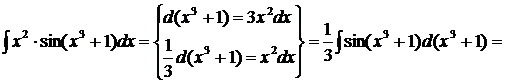
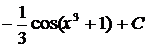2 способ.

.

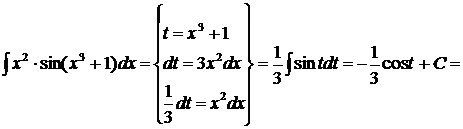
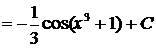Метод интегрирования по частям

Пусть функции 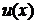и и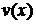меют непрерывные производные на заданном интервале, тогда справедлива формула интегрирования по частям:

.

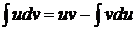Метод интегрирования по частям целесообразно применять в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен, при этом за 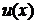берется та функция, которая при дифференцировании упрощается, а за 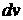берется та часть подынтегрального выражения, интеграл от которой известен или может быть найден.

Выделяют следующие типы интегралов, которые удобно вычислять методом интегрирования по частям:

1. 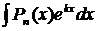, , 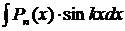, 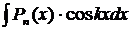где 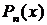- многочлен степени 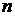, 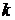– число.

При вычислении данных интегралов формулу применяют n раз, обозначив за .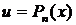

2. , , , , .

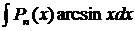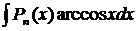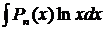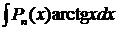При вычислении интегралов второго типа удобно обозначить за .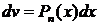

3. 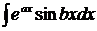, , 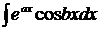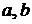– числа.

В данном случае обозначают .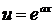

Примеры.

1.

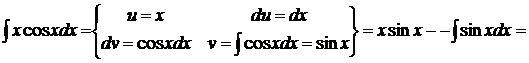
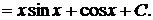
2.

.

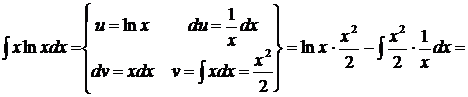
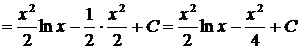Иногда формулу интегрирования по частям приходится применять более одного раза.

Пример.

.

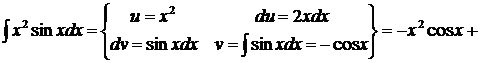
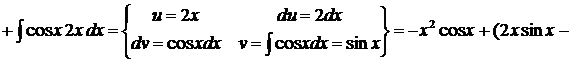
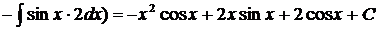Интегрирование простейших рациональных дробей

1. Интегралы вида 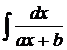сводят к табличным заменой .

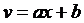2. Интегралы вида 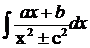разбиваются на сумму двух интегралов 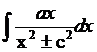и 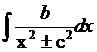. Первый решается заменой 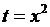. А второй представляет собой табличный интеграл.

3. Интегралы вида 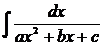решаются с помощью выделения полного квадрата в знаменателе

.

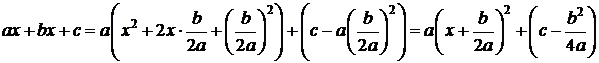Аналогично решаются интегралы вида .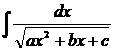

Интегрирование простейших видов иррациональностей

Пример. Вычислим интеграл .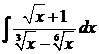

Подынтегральная функция рациональным образом зависит от 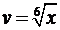, поскольку её можно записать в виде

.

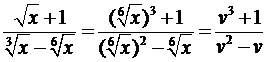Сделаем замену :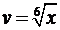

.

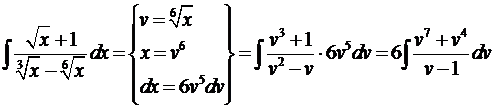Получили интеграл от рациональной дроби 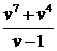, которая является неправильной дробью, поскольку степень её числителя, равная 7, больше степени знаменателя, равной 1. Значит, нужно выделить в этой дроби целую часть. Для этого разделим числитель на знаменатель «столбиком» неправильная дробь представляется в виде

.

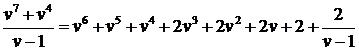Теперь можно вычислить интеграл:

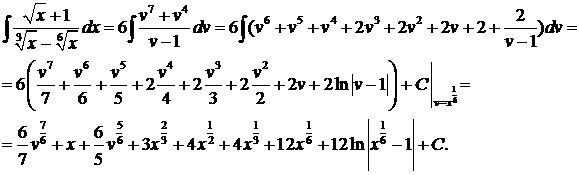
Определенный интеграл

Пусть функция 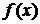определена и ограничена на 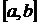и 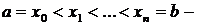произвольное разбиение этого отрезка на 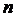элементарных отрезков. На каждом отрезке 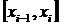выберем точку 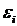. Тогда сумма 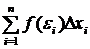называется интегральной суммой для функции 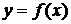на отрезке .

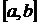Если предел интегральной суммы 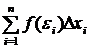при стремлении 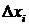к нулю существует и конечен, то он называется определенным интегралом от функции 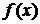в пределах от 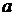до 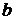и обозначается:

.

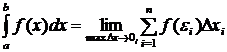Определенный интеграл не должен зависеть от способа выбора точек 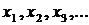и точек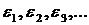

Для вычисления определенного интеграла используется формула Ньютона-Лейбница:

,

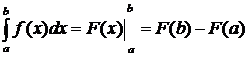где 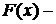любая первообразная функции 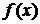на отрезке .

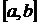Таким образом, при вычислении определенного интеграла с использованием формулы Ньютона-Лейбница сначала, используя технику нахождения неопределенного интеграла, находят первообразную 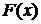для подынтегральной функции 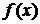, а затем вычисляют приращение первообразной на данном отрезке.

Примеры.

1.

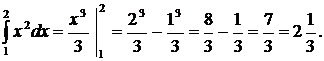
2.