Теоретические сведения к выполнению контрольной работы
Вычисление пределов функции
Пусть функция 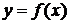 определена в некоторой окрестности точки
определена в некоторой окрестности точки 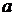 . Число
. Число 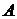 называется пределом функции
называется пределом функции 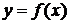 при
при 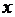 , стремящемся к
, стремящемся к 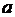 (в точке
(в точке 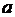 ), если для любого
), если для любого 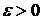 существует
существует 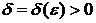 такое, что при
такое, что при 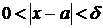 справедливо неравенство
справедливо неравенство 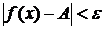 .
.
В этом случае пишут: 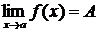 .
.
В самой точке 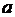 функция
функция 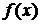 может и не существовать. Аналогично, запись
может и не существовать. Аналогично, запись 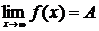 обозначает, что для любого
обозначает, что для любого 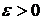 существует число
существует число 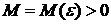 такое, что при
такое, что при 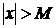 выполняется неравенство
выполняется неравенство 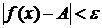 .
.
При вычислении пределов применяются следующие теоремы:
I. Если точка 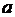 принадлежит области определения функции
принадлежит области определения функции 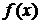 , то
, то 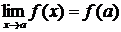 .
.
II. Если существуют конечные пределы 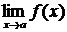 (или
(или 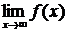 ) и
) и 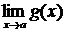 (или
(или 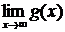 ), то
), то
1. 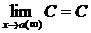 , где
, где 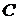 – постоянная.
– постоянная.
2. 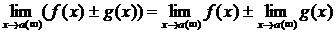 .
.
3.  .
.
4. 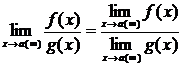 , если
, если 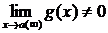 .
.
Полагают, что 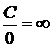 ,
, 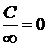 , где
, где 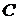 – постоянная, причем
– постоянная, причем 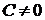 .
.
Вычисление предела 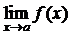 , где
, где 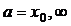 , начинают всегда с подстановки в
, начинают всегда с подстановки в 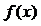 предельного значения её аргумента
предельного значения её аргумента 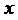 . В процессе вычисления пределов могут возникать неопределенности вида
. В процессе вычисления пределов могут возникать неопределенности вида 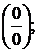

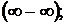
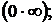
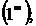
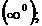
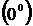 . В простейших случаях они раскрываются с помощью алгебраических преобразований.
. В простейших случаях они раскрываются с помощью алгебраических преобразований.
Пример. Найти 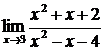 .
.
Решение. Используя теоремы о пределах, получим:
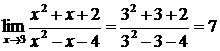 .
.
Ответ: 7.
Для раскрытия неопределенности 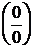 при
при 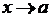 , если она задана отношением двух многочленов, сначала раскладывают на множители числитель и знаменатель, а затем сокращают на
, если она задана отношением двух многочленов, сначала раскладывают на множители числитель и знаменатель, а затем сокращают на 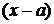 . При этом обычно используют формулы сокращенного умножения:
. При этом обычно используют формулы сокращенного умножения:
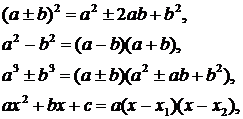
где 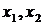 – корни квадратного уравнения
– корни квадратного уравнения 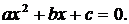
В квадратном трёхчлене 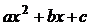 множитель выделяют разложением квадратного трёхчлена по формуле
множитель выделяют разложением квадратного трёхчлена по формуле 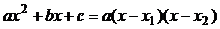 , где
, где 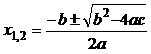 .
.
В выражении 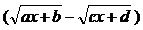 множитель выделяют следующим способом:
множитель выделяют следующим способом: 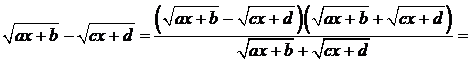
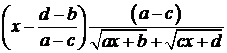
Пример. Найти 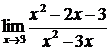 .
.
Решение. При подстановке в выражение, стоящего под знаком предела предельного значения 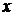 равного 3, получаем неопределенность
равного 3, получаем неопределенность  . Для разложения числителя на множители решаем квадратное уравнение
. Для разложения числителя на множители решаем квадратное уравнение 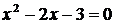 и находим корни
и находим корни 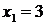 и
и 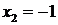 . Следовательно,
. Следовательно, 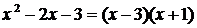 . В знаменателе выносим
. В знаменателе выносим 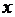 за скобку, получим
за скобку, получим 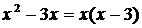 .После сокращения дроби на
.После сокращения дроби на 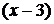 и подстановки в полученное выражение предельного значения
и подстановки в полученное выражение предельного значения 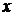 , равного 3, получим:
, равного 3, получим:
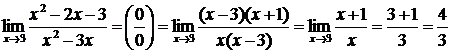 .
.
Ответ: 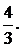
Пример.Найти 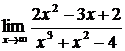 .
.
Решение. Имеем неопределенность вида  . Чтобы раскрыть ее, разделим числитель и знаменатель дроби на наибольшую степень
. Чтобы раскрыть ее, разделим числитель и знаменатель дроби на наибольшую степень 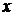 , то есть на
, то есть на 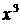 . Знаменатель полученной дроби при
. Знаменатель полученной дроби при 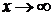 не равен 0, следовательно, применяя теоремы о пределах получим:
не равен 0, следовательно, применяя теоремы о пределах получим:
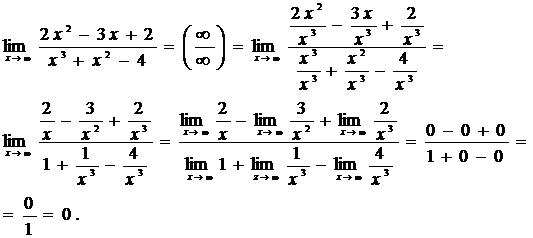
Ответ: 0.
Пример.Найти 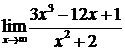
Решение. При подстановке вместо переменной 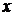 её предельного значения
её предельного значения 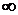 получим неопределённость
получим неопределённость 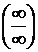 . Для её раскрытия сначала разделим числитель и знаменатель дроби на
. Для её раскрытия сначала разделим числитель и знаменатель дроби на 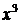 (старшую степень переменной
(старшую степень переменной 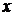 в числителе и знаменателе), после чего используем свойства конечных пределов и бесконечно больших функций. Получим
в числителе и знаменателе), после чего используем свойства конечных пределов и бесконечно больших функций. Получим 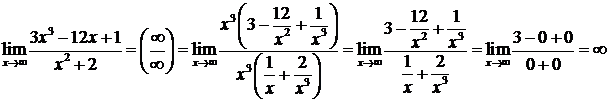
Пример.Найти 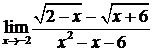
Решение.При подстановке вместо переменной 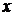 её предельного значения
её предельного значения 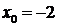 получим неопределённость
получим неопределённость  . Для её раскрытия выделим в числителе и знаменателе дроби общий множитель вида
. Для её раскрытия выделим в числителе и знаменателе дроби общий множитель вида 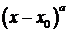 , где
, где 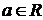 – некоторое число, т.е. множитель
– некоторое число, т.е. множитель 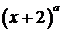 . Затем сократим на него числитель и знаменатель дроби, после чего используем свойства пределов.
. Затем сократим на него числитель и знаменатель дроби, после чего используем свойства пределов.
В результате получим 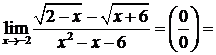
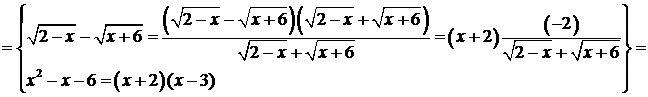
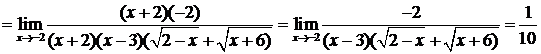 .
.
Для вычисления пределов часто используются первый замечательный предел:
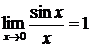
и второй замечательный предел:
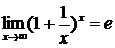
или
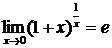 ,
,
а также их следствия:
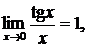
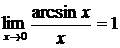 ,
,
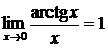 ,
,
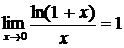 .
.
При вычислении пределов также могут использоваться следующие известные пределы: 
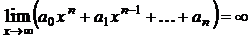 ,
, 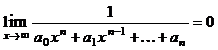 ,
, 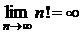 (
( 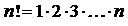 ).
).
Таким образом, для раскрытия неопределённостей  , содержащих тригонометрические и обратные тригонометрические функции, в числителе и знаменателе дроби выделяют сначала множители вида:
, содержащих тригонометрические и обратные тригонометрические функции, в числителе и знаменателе дроби выделяют сначала множители вида: 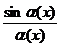 ,
, 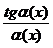 ,
, 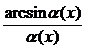 ,
, 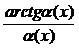 , где
, где 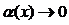 при
при 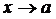 , используя формулы тригонометрии:
, используя формулы тригонометрии: 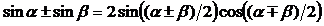 ,
, 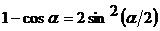 ,
, 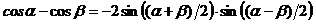 . После чего применяют свойства пределов, учитывая, что:
. После чего применяют свойства пределов, учитывая, что: 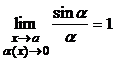 ,
, 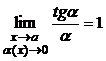 ,
, 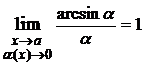 ,
, 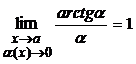 .
.
Для раскрытия неопределённости 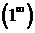 , возникающей при вычислении предела
, возникающей при вычислении предела 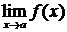 , где
, где 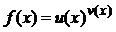 ,
, 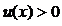 , сначала выражение
, сначала выражение 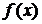 представляют в виде
представляют в виде 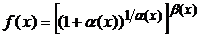 , где
, где 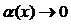 при
при 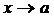 . После чего используют свойства пределов, заменяя выражение
. После чего используют свойства пределов, заменяя выражение 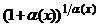 его предельным значением
его предельным значением 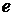 и учитывая, что
и учитывая, что 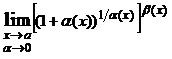 =
= 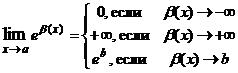 .
.
Пример. Найти 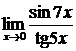 .
.
Решение. Так как под знаком предела 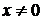 , то числитель умножаем и делим на
, то числитель умножаем и делим на 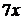 , а знаменатель – на
, а знаменатель – на 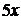 , далее применяем первый замечательный предел и его следствие:
, далее применяем первый замечательный предел и его следствие:
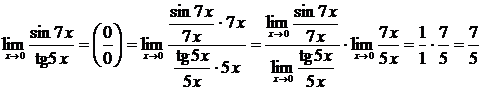 .
.
Ответ: 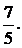
Пример. Найти 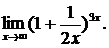
Решение. Выражение, стоящее под знаком предела при 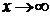 представляет собой неопределенность вида (
представляет собой неопределенность вида ( 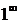 ), раскрываемую с помощью второго замечательного предела. Сделаем замену переменной
), раскрываемую с помощью второго замечательного предела. Сделаем замену переменной 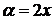 . При
. При 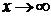 имеем
имеем 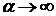 . Следовательно,
. Следовательно,
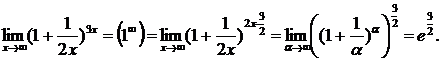
Ответ: 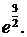
Пример. Найти 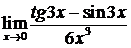
Решение. При подстановке вместо переменной 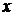 её предельного значения
её предельного значения 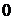 получим неопределённость
получим неопределённость  . Выделим в числителе множители вида
. Выделим в числителе множители вида 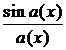 , где
, где 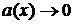 при
при 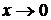 и используем свойства пределов. Получим
и используем свойства пределов. Получим
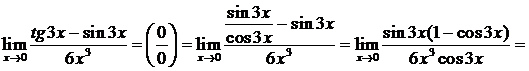
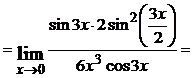
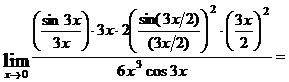
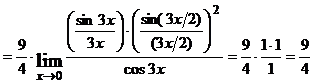 .
.
Пример. Найти 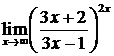
Решение. При подстановке вместо переменной 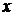 её предельного значения
её предельного значения 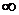 получим неопределённость (
получим неопределённость ( 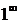 ). Представим
). Представим 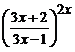 в виде
в виде 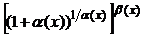 , где
, где 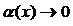 при
при 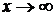 , следующим способом:
, следующим способом:
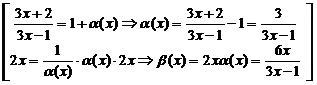
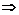
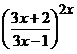 =
= 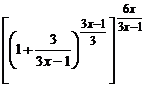 . Тогда учитывая, что
. Тогда учитывая, что 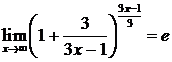 ,
, 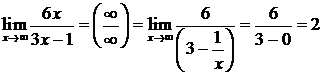 , получим
, получим 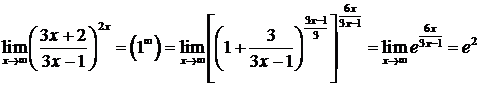 .
.
Непрерывность функции
Функция 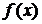 называется непрерывной в точке
называется непрерывной в точке 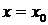 , если для
, если для 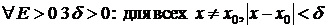 справедливо неравенство
справедливо неравенство 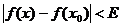 .
.
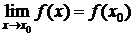 .
.
В определении предела 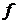 в точке число
в точке число 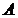 может быть любым числом, в частности
может быть любым числом, в частности 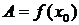 .
.
В определении непрерывности пределом 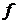 может быть только значение
может быть только значение 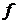 в предельной точке
в предельной точке 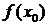 .
.
Непрерывность 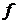 в точке означает выполнение трех условий:
в точке означает выполнение трех условий:
1) существование значения функции 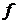 в предельной точке,
в предельной точке,
2) существование предела функции 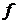 в рассматриваемой точке,
в рассматриваемой точке,
3) значение функции 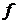 в предельной точке совпадает с пределом функции
в предельной точке совпадает с пределом функции 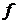 в заданной точке.
в заданной точке.
Если какое-либо из этих условий будет нарушено в заданной точке, то такая точка называется точкой разрыва.
Пример.Дана функция 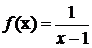
 , выяснить является ли
, выяснить является ли 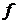 непрерывной в точках
непрерывной в точках 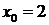
1) 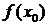 =
= 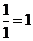
2) 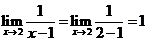
3) 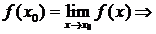 в точке
в точке 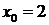 функция
функция 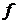 непрерывна.
непрерывна.
Теорема.Сумма, разность, произведение, частное двух непрерывных в точке функций (функция, стоящая в знаменателе 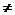 0) также являются непрерывными в точке функциями.
0) также являются непрерывными в точке функциями.
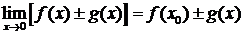
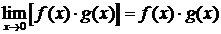
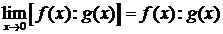 , g(x)
, g(x) 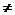 0
0
Определение. 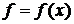 называется непрерывной на отрезке [а;b]если она непрерывна в каждой точке этого отрезка.
называется непрерывной на отрезке [а;b]если она непрерывна в каждой точке этого отрезка.
Точками разрыва функции 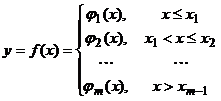 являются точки разрыва функций
являются точки разрыва функций 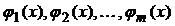 в промежутках
в промежутках 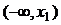 ,
, 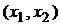 ,…,
,…, 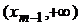 , кроме того, точками возможного разрыва функции
, кроме того, точками возможного разрыва функции 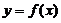 являются точки
являются точки 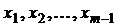 в окрестности которых и в самих точках функция задаётся разными аналитическими выражениями. Точка
в окрестности которых и в самих точках функция задаётся разными аналитическими выражениями. Точка 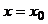 является точкой непрерывности функции
является точкой непрерывности функции 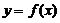 тогда и только тогда, когда:
тогда и только тогда, когда: 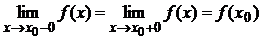 .
.
Пример.Для указанной функции 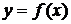 требуетсянайтиточки разрыва функции и исследовать их характер.Построить график функции.
требуетсянайтиточки разрыва функции и исследовать их характер.Построить график функции.
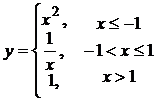 .
.
Решение. Функции 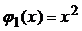 и
и 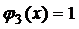 непрерывны в промежутках
непрерывны в промежутках 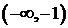 и
и 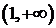 как элементарные функции, определённые в каждой точке данных промежутков, а функция
как элементарные функции, определённые в каждой точке данных промежутков, а функция 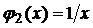 в промежутке
в промежутке 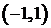 имеет точкой разрыва точку
имеет точкой разрыва точку 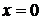 , в которой она не определена. Тогда для функции
, в которой она не определена. Тогда для функции 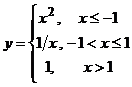 точка
точка 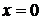 является точкой разрыва, а точки
является точкой разрыва, а точки 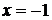 и
и 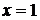 , в окрестности которых и в самих точках функция задаётся разными аналитическими выражениями, являются точками возможного разрыва.
, в окрестности которых и в самих точках функция задаётся разными аналитическими выражениями, являются точками возможного разрыва.
Исследуем на непрерывность точки 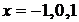 :
:
1) 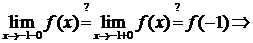
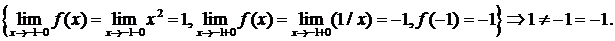
Следовательно, точка 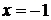 – точка разрыва 1-го рода функции
– точка разрыва 1-го рода функции 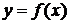 .
.
2) 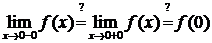
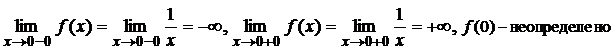 Следовательно, точка
Следовательно, точка 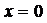 – точка бесконечного разрыва (2-го рода) функции
– точка бесконечного разрыва (2-го рода) функции 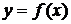 .
.
3) 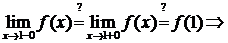
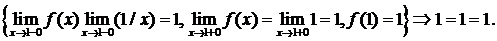
Следовательно, точка 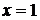 – точка непрерывности функции
– точка непрерывности функции 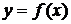 .
.
График функции 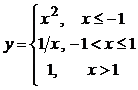 имеет вид, изображённый на рисунке.
имеет вид, изображённый на рисунке.
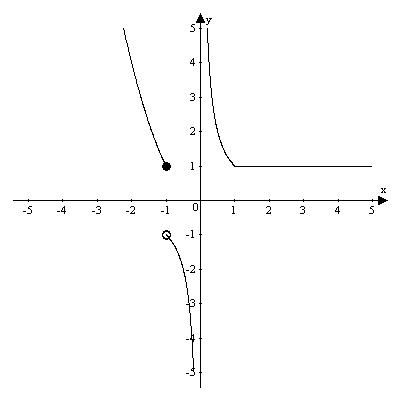
Ответ. 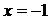 – точка разрыва 1-го рода,
– точка разрыва 1-го рода, 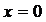 –точка бесконечного разрыва функции
–точка бесконечного разрыва функции 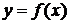 , в точке
, в точке 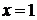 функция непрерывна.
функция непрерывна.
Производная
Приращением функции 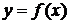 называется разность
называется разность 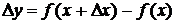 , где
, где 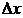 – приращение аргумента
– приращение аргумента 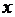 .
.
Если существует конечный предел отношения приращения функции 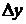 к приращению аргумента
к приращению аргумента 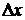 при произвольном стремлении
при произвольном стремлении 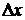 к нулю, то этот предел называется производной функции
к нулю, то этот предел называется производной функции 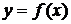 в точке
в точке 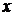 :
: 
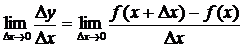 .
.
Обозначается производная одним из следующих символов:

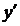 ,
, 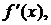
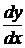 .
. 
Если указанный предел существует, то функция 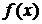 является дифференцируемой в точке х.
является дифференцируемой в точке х.
Правила дифференцирования
Пусть 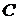 – постоянное число,
– постоянное число, 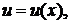
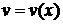 – некоторые дифференцируемые функции, тогда
– некоторые дифференцируемые функции, тогда
1. 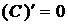 ,
,
2. 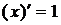 ,
,
3. 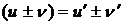 ,
,
4. 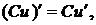
5. 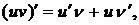
6. 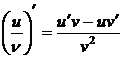
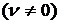 ,
,
7. 
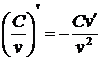 ,
,