Полярная система координат. Связь между полярными и прямоугольными координатами.

Полярная система координат задается точкойО, называемой полюсом, лучом Оp,

φ

О

р

r

M(r;φ)

Рис. 24.

называемой полярной осью, и единичным вектором 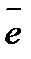того же направления, что и луч Оp.

Возьмем на плоскости точку М, не совпадающую с О. Положение точки М определяется двумя числами: ее расстоянием r от полюса О и угломφ, образованным отрезком ОМ с полярной осью (отсчет углов ведется в направлении, противоположном движению часовой стрелки) (см. рис. 24).

Числа r и φ называются полярными координатами точки М, пишут 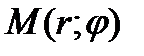, при этом r называют полярным радиусом, φ – полярным углом.

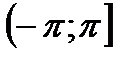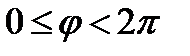Для построения всех точек плоскости достаточно полярный угол φ ограничить промежутком (или ), а полярный радиус – 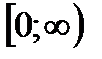. В этом случае каждой точке плоскости (кроме О) соответствует единственная пара чисел r и φ, и обратно.

Установим связь между прямоугольными и полярными координатами. Для этого совместим полюсО с началом координат системы Оху, а полярную ось с положительной полуосью Ох. Пусть х и у – прямоугольные координаты точки М, а rи φ – ее полярные координаты.

О

М

x

p

y

φ

r

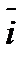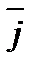Рис. 25.

Из рисунка 25 видно, что прямоугольные координаты точки М выражаются через полярные координаты точки следующим образом:

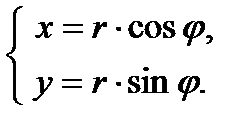
Полярные же координаты точки Мвыражаются через ее декартовы координаты (тот же рисунок) такими формулами:

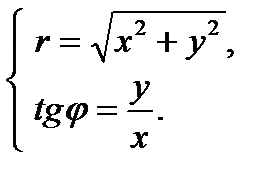
Определяя величину φ, следует установить (по знакам х и у) четверть, в которой лежит искомый угол, и учитывать, что .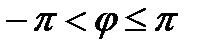

Пример 9.1. Дана точка 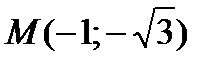. Найти полярные координаты точки М.

Решение: Находим r и φ:

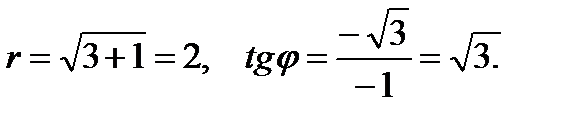
Отсюда 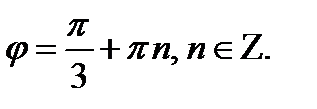Но так как точка М лежит в 3-й четверти, то 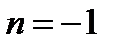и 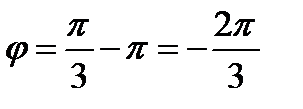. Итак, полярные координаты точки М есть 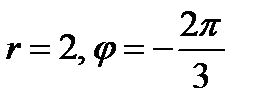, т.е. .

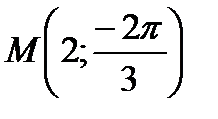Общее уравнение прямой на плоскости. Частные случаи. Нормальный вектор прямой.

Общее уравнение прямой

Рассмотрим уравнение первой степени относительно х и у в общем виде

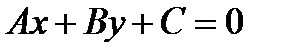, (10.4)

гдеА, В, С – произвольные числа, причем А и В не равны нулю одновременно.

Покажем, что уравнение (10.4) есть уравнение прямой линии. Возможны два случая.

ЕслиВ = 0, то уравнение (10.4) имеет вид 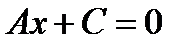, причем 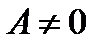, т.е. 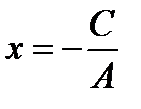. Это есть уравнение прямой, параллельной оси Оу и проходящей через точку .

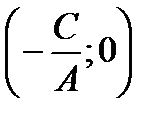Если 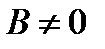, то из уравнения (10.4) получаем 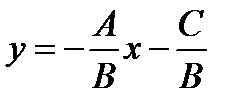. Это есть уравнение прямой с угловым коэффициентом .

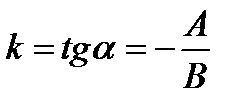Итак, уравнение (10.4) есть уравнение прямой линии, оно называется общим уравнением прямой.

Некоторые частные случаи общего уравнения прямой:

1) еслиА = 0, то уравнение приводится к виду 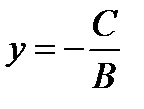. Это есть уравнение прямой, параллельной оси Ох;

2) еслиВ= 0, то прямая параллельна оси Оу;

3) еслиС= 0, то получаем 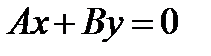. Уравнению удовлетворяют координаты точки 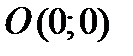, прямая проходит через начало координат.

Найдем уравнение прямой, проходящей через заданную точку 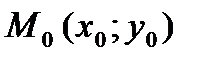перпендикулярно данному ненулевому вектору .

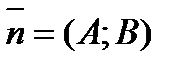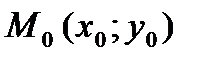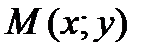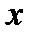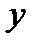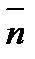Рис. 43.

Возьмем на прямой произвольную точку 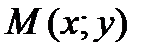и рассмотрим вектор 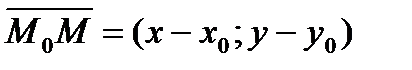(см. рис. 43). Поскольку векторы 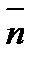и 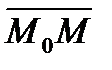перпендикулярны, то их скалярное произведение равно нулю: 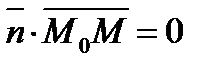, то есть

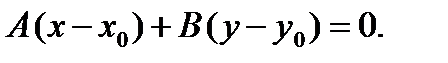(10.8)

Уравнение (10.8) называется уравнением прямой, проходящей через заданную точку перпендикулярно заданному вектору.

Вектор 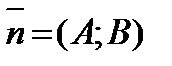, перпендикулярной прямой называется нормальным вектором этой прямой.

Уравнение (10.8) можно переписать в виде

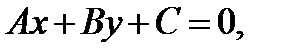(10.9)

гдеА и В – координаты нормального вектора, 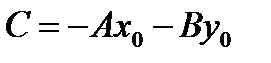– свободный член. Уравнение (10.9) есть общее уравнение прямой