Невырожденные матрицы. Алгоритм нахождения обратной матрицы.
Невырожденные матрицы. Алгоритм нахождения обратной матрицы.
Основные понятия
Пусть А – квадратная матрица n-го порядка.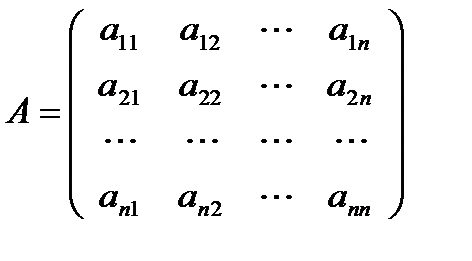 
Квадратная матрица А называется невырожденной, если определитель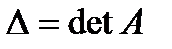 
не равен нулю: 
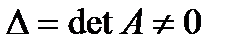. В противном случае ( 
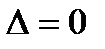) матрица А называется вырожденной.
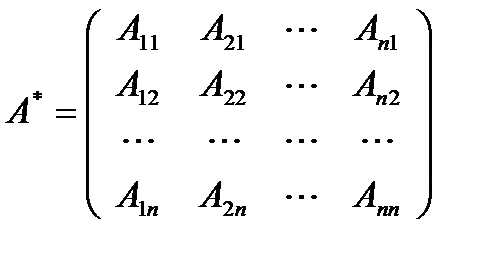Матрицей, союзной к матрице А, называется матрица
где -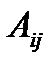 
алгебраическое дополнение элемента 
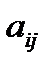данной матрицы А (оно определяется так же, как и алгебраическое дополнение элемента определителя).
Матрица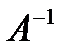 
называется обратной матрице А, если выполняется условие: 
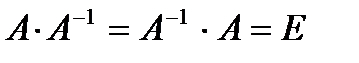, (3.1) где Е – единичная матрица того же порядка, что и матрица А. Матрица 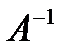имеет те же размеры, что и матрица А.
Теорема 3,1 Всякая невырожденная матрица имеет обратную
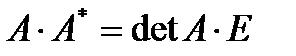(3.2) 
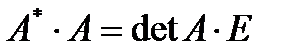. (3.3)Равенства (3.2) и (3.3) перепишем в виде 
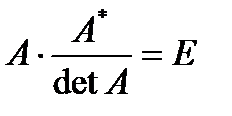и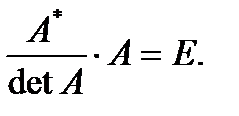 
Сравнивая полученные результаты с определением (3.1), получим 
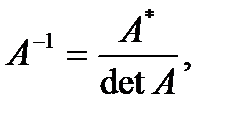т.е.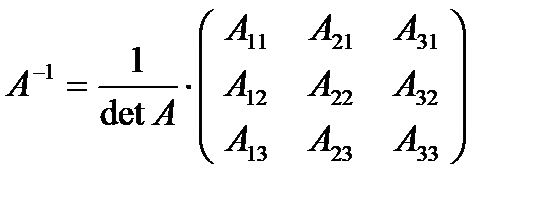 
.Отметим свойства обратной матрицы: 1. 
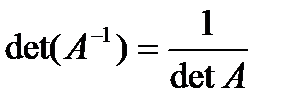; 2. 
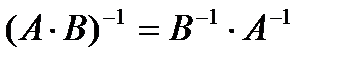;3.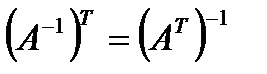 
.
Определители 2-го и 3-го порядка и методы их вычисления. Примеры.
Понятие определителя - число, характеризующее квадратную матрицу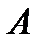 
, необходимо для решения систем линейных алгебраических уравнений.
Определитель матрицы 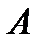обозначают 
, 
, 
.
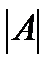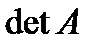1) Определителем матицы 1-го порядка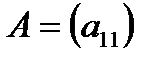 
, называется элемент 
: 
;
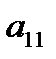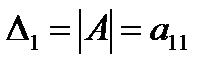2) Определителем матрицы 2-го порядка называется число, вычисляемое по формуле:
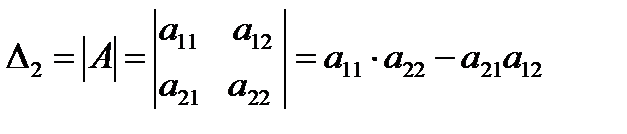. Произведения 
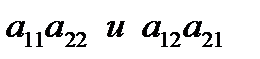называются членами определителя 2-го порядка.
3) Определителем матрицы 3-го порядка называется число, вычисляемое по формуле:
.
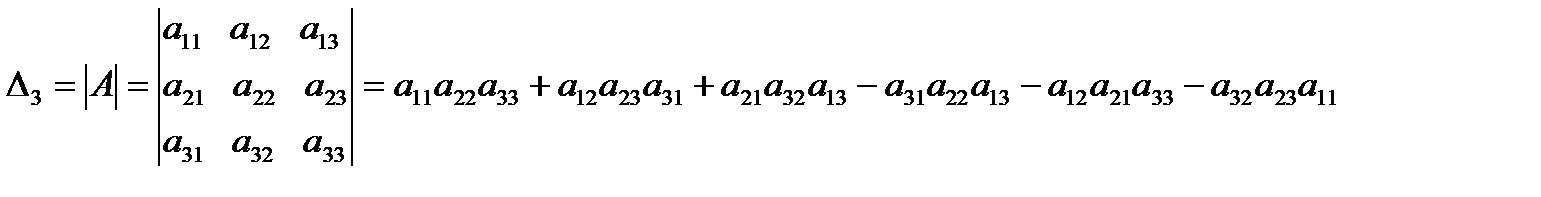Данная формула получила название правила треугольников или правило Саррюса.
Определители. Свойства определителей.
Сформулируем основные свойства определителей, присущие определителям всех порядков. Некоторые из этих свойств поясним на определителях 3-го порядка.
Свойство 1 («Равноправность строк и столбцов»). Определитель не изменяется, если его строки заменить столбцами, и наоборот.
Иными словами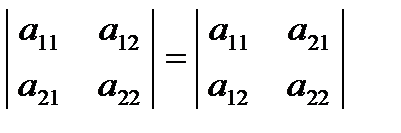 
, 
.
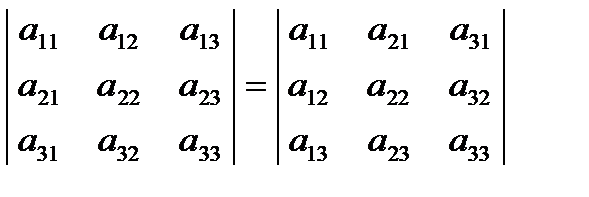Свойство 2. При перестановке двух параллельных рядов определитель меняет знак.
Свойство 3. Определитель, имеющий два одинаковых ряда, равен нулю.
Свойство 4. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.
Из свойств 3 и 4 следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.
Действительно,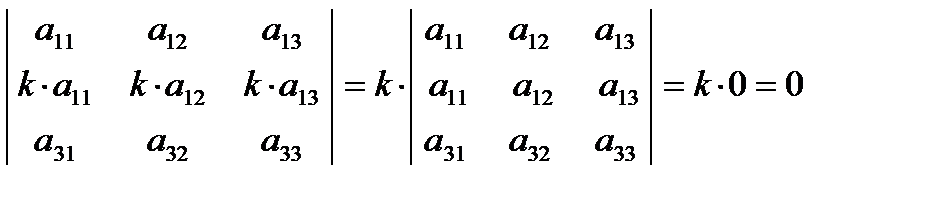 
.
Свойство 5. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.
Например,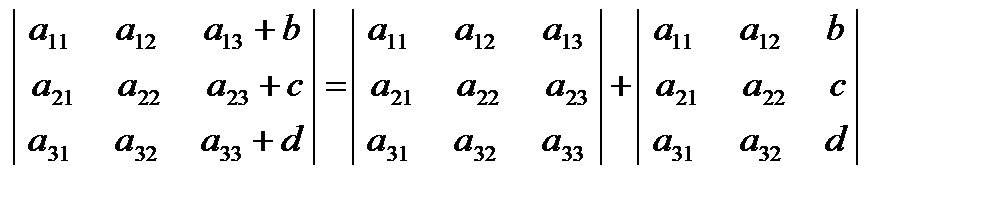 
.
Свойство 6. («Элементарные преобразования определителя»). Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на одно и то же число.
Пример 2.3. Доказать, что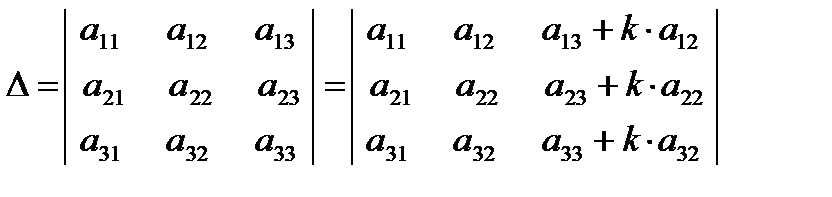 
.Решение: Действительно, используя свойства 5, 4 и 3 получим 
.
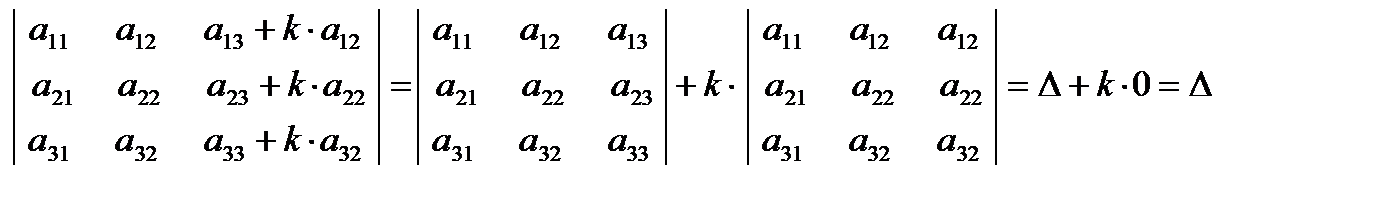Дальнейшие свойства определителя связаны с понятиями минора и алгебраического дополнения.
Невырожденные матрицы. Алгоритм нахождения обратной матрицы.
Основные понятия
Пусть А – квадратная матрица n-го порядка.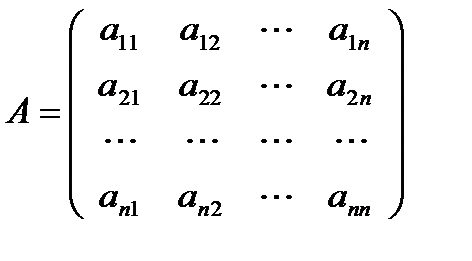
Квадратная матрица А называется невырожденной, если определитель 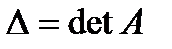не равен нулю: 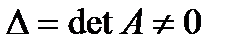. В противном случае ( 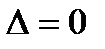) матрица А называется вырожденной.
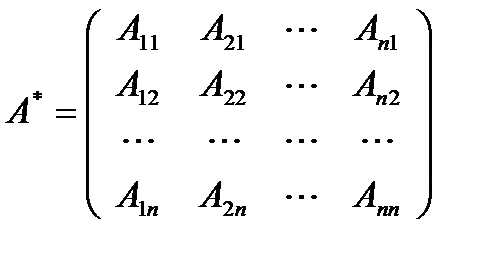Матрицей, союзной к матрице А, называется матрица
где - 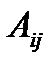алгебраическое дополнение элемента 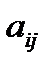данной матрицы А (оно определяется так же, как и алгебраическое дополнение элемента определителя).
Матрица 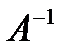называется обратной матрице А, если выполняется условие: 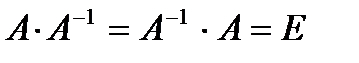, (3.1) где Е – единичная матрица того же порядка, что и матрица А. Матрица 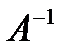имеет те же размеры, что и матрица А.
Теорема 3,1 Всякая невырожденная матрица имеет обратную
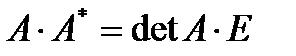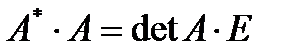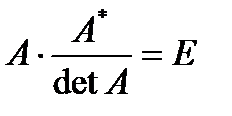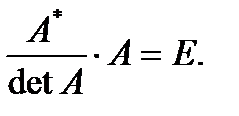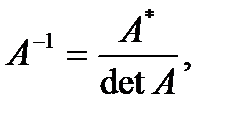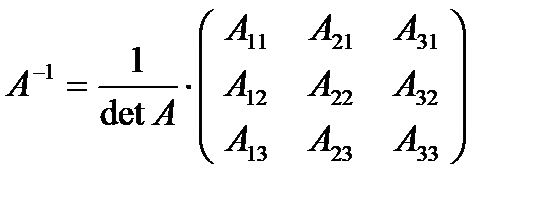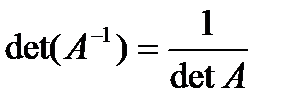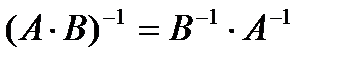(3.2) . (3.3)Равенства (3.2) и (3.3) перепишем в виде и Сравнивая полученные результаты с определением (3.1), получим т.е. .Отметим свойства обратной матрицы: 1. ; 2. ;3. .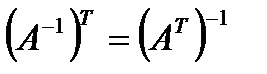
Определители 2-го и 3-го порядка и методы их вычисления. Примеры.
Понятие определителя - число, характеризующее квадратную матрицу 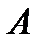, необходимо для решения систем линейных алгебраических уравнений.
Определитель матрицы 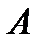обозначают , , .
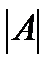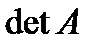1) Определителем матицы 1-го порядка 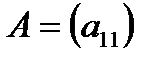, называется элемент : ;
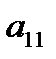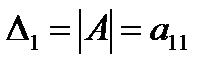2) Определителем матрицы 2-го порядка называется число, вычисляемое по формуле:
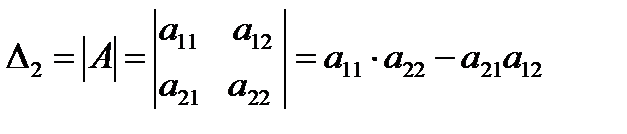. Произведения 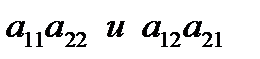называются членами определителя 2-го порядка.
3) Определителем матрицы 3-го порядка называется число, вычисляемое по формуле:
.
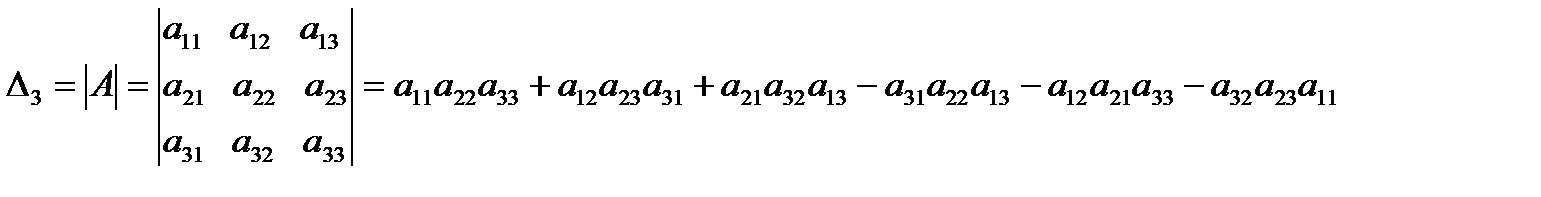Данная формула получила название правила треугольников или правило Саррюса.