Параметрические уравнения прямой на плоскости (с выводом) и их физический смысл.

30. Угол между двумя прямыми на плоскости, заданными общими уравнениями (с выводом формулы угла). Условия параллельности и перпендикулярности прямых.

31. Угол между двумя прямыми на плоскости, заданными каноническими уравнениями (с выводом формулы угла). Условия параллельности и перпендикулярности прямой.

I) Пусть две прямые заданы общим уравнением:

Угол между ними есть угол между их нормальными векторами.

формула угла между и .

Если и

Если

II.Пусть прямые заданы каноническими уравнениями:

Угол между ними есть угол между их направляющими векторами.

формула угла между и .

Если и

Если же

III.Пусть прямые заданы с угловыми коэффициентами:

y

x

0

Пусть – угол между и , т.е. Ясно, что Тогда tg

Если , то , а тогда т.е. условие

Если же

Определение углового коэффициента прямой. Уравнения прямых с угловыми коэффициентами (с выводами).

Угловым коэффициентом к прямой l называется тангенс угла наклона этой прямой с положительным направлением оси Ox:

Если

Если l:

1. Если y

0x

2. Если

y

x

3. Если

y

x

4. Если

y

x

Перепишем общее уравнение –уравнение lck.

Пусть тогда выполняется равенство

Отнимая почленно от равенство получим – уравнение lckпроходящий через фиксированную точку

Окружность: определение, общее и частные уравнения, понятия хорды, диаметра, формула длины окружности, схематические изображения.

Окружностью называется геометрическое место точек (г.м.т.) на плоскости, равноудаленных от одной точки, называемой её центром. Пусть

уравнение окружности с центром в точке 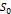и радиуса r.

Если , то

Если , то и окружность называется единичной.

Хордойназывается любой отрезок, соединяющий две точки окружности.

Хорда проходящая через центр называется диаметром.

Отрезок соединяющий любую точку окружности с центром называетсярадиусом.

Если d –диаметр, то d = 2r, или

34. Эллипс: определение, каноническое уравнение, фокусы, вершины, эксцентриситет, оси и уравнения директрис. Схематические изображения.

Эллипс – это геометрическое место точек на плоскости, сумма расстояний от каждой из который до 2 точек называемые фокусами, если величина постоянная (равная 2а).

Согласно определению:

Отношение называетсяэксцентриситетом эллипса.

Прямые называются директрисами эллипса.

Так как

Для окружности

Гипербола: определение, каноническое уравнение, фокусы, вершины, оси уравнения асиматог и директрис, свойства. Понятия равнобочной и сопряженной гипербол. Схематические изображения.

Парабола: определение, каноническое уравнение, фокус, эксцентриситет, директриса, ось симметрии. Различные виды парабол, схематические изображения.