Векторы и линейные операции над ними: сложение, вычитание, умножение вектора на число. Схематические изображения.

Вектор – это направленный отрезок.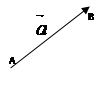

Векторы могут обозначаться как 2-мя прописными буквами, так и одной строчной с чертой или стрелкой.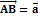

Длина вектора называется его модулем и обозначается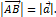

Если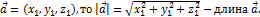

Если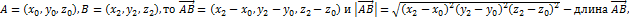

Векторы, лежащие на одной прямой или на параллельных прямых, называют коллинеарными.

Если начало и конец вектора совпадают 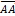, то такой вектор называется нулевым и обозначается 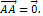Длина нулевого вектора равна нулю: 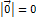, а направление – неопределенно.

Сложение векторов

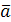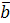Суммой двух векторов и называется вектор 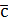, начало которого совпадает с началом вектора 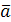, а конец – с концом вектора 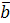, отложенного из конца вектора 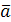(правило треугольника).

Суммой векторов 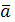и 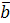называется такой третий вектор 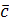, что при совмещенных началах этих трех векторов, векторы 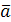и 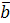служат сторонами параллелограмма, а вектор 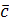– его диагональю (называется сложением по правилу параллелограмма).

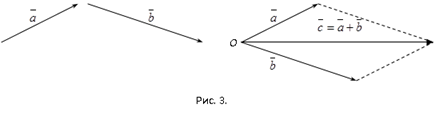
Сумма любого конечного числа векторов может быть найдена по правилу многоугольника: чтобы построить сумму конечного числа векторов, достаточно совместить начало каждого последующего вектора с концом предыдущего и построить вектор, соединяющий начало первого вектора с концом последнего.

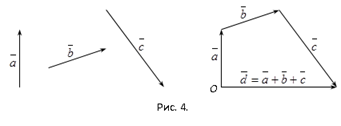
При сложении векторов выполняется переместительныйзакон, т.е. + = +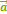

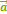
и сочетательныйзакон, т.е. ( + )+ = +( + )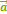

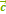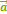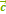Вычитание векторов

Под разностью векторов 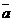и 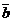понимается вектор 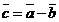такой, что 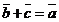(см. рис. 5).

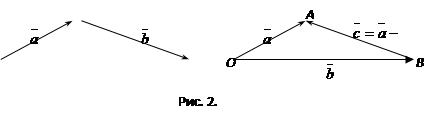
Умножение вектора на число

Произведением вектора 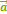на число k называется такой вектор , длина которого равна |k|⋅| 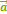|, причем векторы сонаправлены, если k>0, и противоположно направлены, если k<0.

Произведение нулевого вектора на любое число есть нулевой вектор.

Обозначение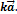

Вектора 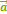и 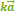коллинеарны для любого k. Если два вектора 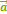и коллинеарны – то существует такое число k, что 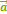=k .
Произведение любого вектора на число нуль есть нулевой вектор.

Для любых векторов 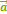и и чисел k и l справедливы следующие законы:

Сочетательный: (kl)a→=k(l )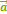

Первый распределительный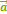: k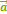( + )=k +k

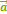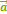Второй распределительный: (k+l) =k +l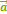

Разложение вектора по базисным ортам. Направляющие косинусы. Длины векторов. Примеры.

Единичные векторы 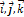выходящие из начала координат в положительных направлениях осей OX, OYи OZназываются ортами этих осей.

Любой вектор 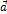можно разложить по ортам осей координат: 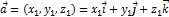, или

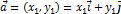(на плоскости).

Пример:

Задание. Вектор 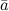задан своими координатами: 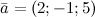. Записать разложение данного вектора по ортам осей координат.

Решение.

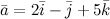
Числа 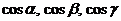называются направляющими косинусами вектора .

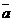Направляющие косинусы вектора 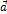определяются соотношениями:

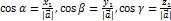, ясно что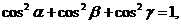

Пример: а = (3; -6; 2).

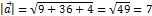
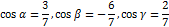
Длина вектора называется его модулем и обозначается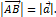

Если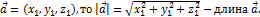

Если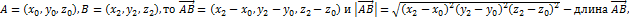

Пример: а = (3; -6; 2).

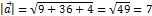
17. Ортогональные, коллинеарные и компланарные векторы: определения и примеры. Условия ортогональности, коллинеарности и компланарности.

Два вектора называются ортогональными, если в пересечении они образуют прямой угол, т.е. угол в 90^о.

Два вектора называются коллинеарными, если они лежат на одной прямой либо на параллельных прямых.

Три вектора называются компланарными , если они лежат в одной плоскости либо в параллельных плоскостях.

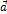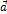Условие ортогональности векторов. Два вектора и ортогональны (перпендикулярны), если их скалярное произведение равно нулю. · = 0

Условия коллинеарности

Ø Два вектора a и b коллинеарны, если существует число n такое, что
a = n · b

Ø Два вектора коллинеарны, если отношения их координат равны.

Ø Два вектора коллинеарны, если их векторное произведение равно нулевому вектору.

Условия компланарности векторов

Ø Три вектора компланарны если их смешанное произведение равно нулю.

Ø Три вектора компланарны если они линейно зависимы.

Ø Для n векторов. Вектора компланарны если среди них не более двух линейно независимых векторов.

(НУЖНЫ ПРИМЕРЫ)