Матричный метод решения состоит в следующем.

Пусть дана система линейных уравнений с nнеизвестными:

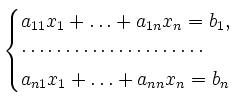
Её можно переписать в матричной форме: AX = B, где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:

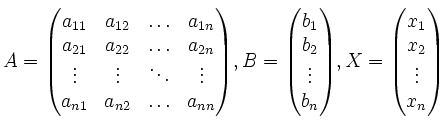
Умножим это матричное уравнение слева на A^-1 — матрицу, обратную к матрице A: A^-1 (AX) = A^-1 B

Так как A^-1A = E, получаем X = A^-1B. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A: detA≠ 0.

Для однородной системы линейных уравнений, то есть когда вектор B = 0, действительно обратное правило: система AX = 0 имеет нетривиальное (то есть не нулевое) решение только если detA = 0. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.

Пример решения неоднородной системы линейных алгебраических уравнений.

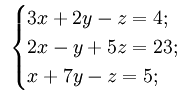
Убедимся в том, что определитель матрицы, составленный из коэффициентов при неизвестных системы линейных алгебраических уравнений не равен нулю.

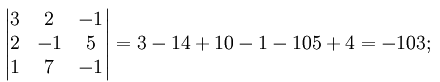
Следующим шагом будет вычисление алгебраических дополнений для элементов матрицы, состоящей из коэффициентов при неизвестных. Они понадобятся для нахождения обратной матрицы.

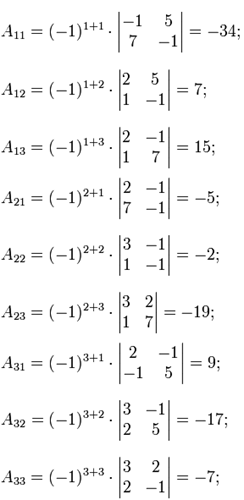
Теперь найдём союзную матрицу и транспонируем её, потом подставим в формулу для нахождения обратной матрицы.

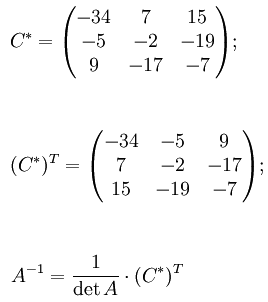
Подставляя переменные в формулу, получаем:

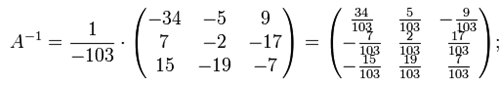
Найдем неизвестные. Для этого перемножим обратную матрицу и столбец свободных членов.

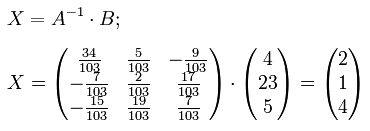
Итак, x=2; y=1; z=4.

5.ФормулыКрамера.

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение. Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители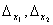

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

.

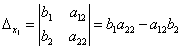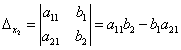Формулы Крамера для нахождения неизвестных:

.

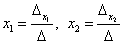Найти значения 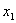и 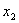возможно только при условии, если

.

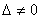Этот вывод следует из следующей теоремы.

Теорема Крамера. Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

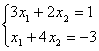. (2)

Согласно теореме Крамера имеем:

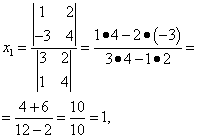
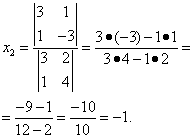
Итак, решение системы (2):

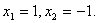
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера.