Модель М/М/m/0/N или модель Энгсета
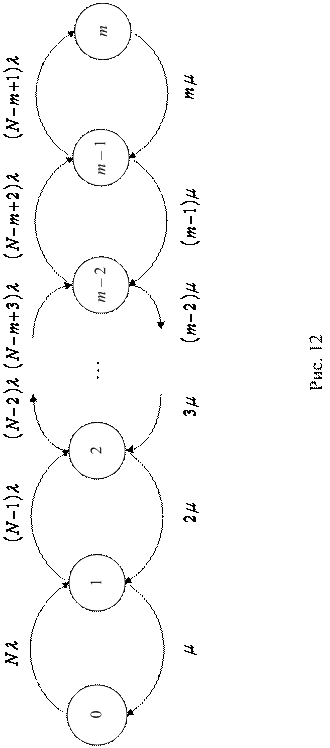
Модель системы массового обслуживания, представленную в настоящем разделе, можно назвать замкнутой версией модели Эрланга. Соответствующий граф состояний имеет вид, изображенный на
рис. 12. Мы будем предполагать, что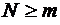 
, в этом случае требова-ноя, поступившие в систему тогда, когда в ней уже имеется 
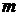требований, теряются и немедленно возвращаются обратно в источник, то есть в группу поступающих так, как будто бы они были полностью обслужены, в итоге очередь в системе отсутствует. В символике Кендалла данная СМО имеет очевидное обозначение М/М/m//0. Очевидно, что для этой модели 
.
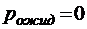Решение уравнений Колмогорова для этого случая имеет вид, очевидно,
, 
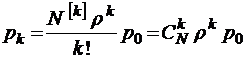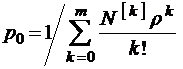
(распределение Энгсета).
Числовые характеристики установившегося режима
Вероятность отказа в данном случае находятся из соотношения
,
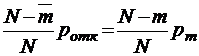откуда следует
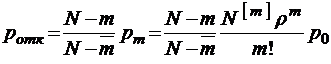. (3.3.1)
Вероятность обслуживания
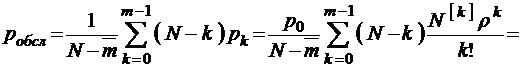
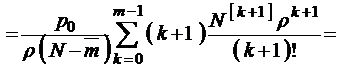
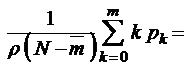
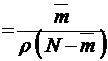, (3.3.2)
относительная пропускная способность, как всегда,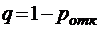 
. Абсолютная пропускная способность в этом случае, очевидно,
.
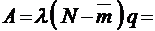
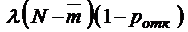
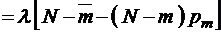Приведем еще один, более строгий, а иногда и более удобный, вывод этого же соотношения:
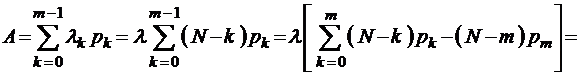
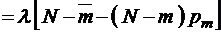. (3.3.3)
Заметим, что для открытых систем массового обслуживания с потерями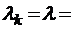 
const, формула (3.3.3) переходит в решение 
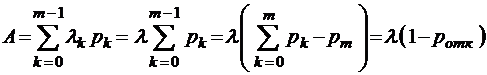, согласно результатам, полученным в § 2.3.
Среднее число требований, одновременно находящихся под обслуживанием (среднее число занятых линий),
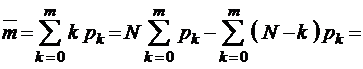
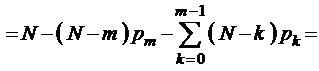
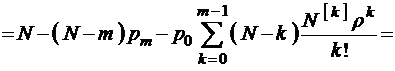
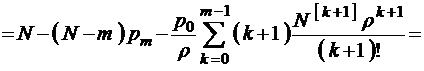
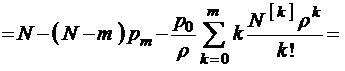
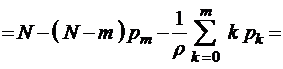
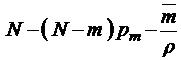. (3.3.4)
Этот же результат можно получить и непосредственно из формулы (3.3.3), поскольку
.
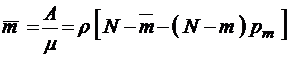Отсюда
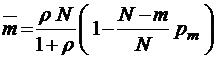
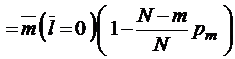. (3.3.5)
При этом, очевидно,
;
.
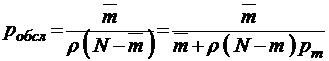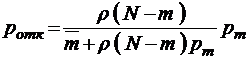Как и следовало ожидать, при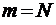 
соотношение (3.3.5) переходит в (3.2.3), а формула (3.3.3) – в зависимость 
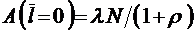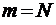. При имеем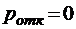 
, 
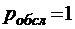. С помощью полученных соотношений легко проверить справедливость формул (3.3.1) и (3.3.2):
.
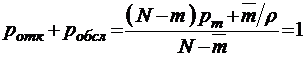Для формулы второго нулевого момента имеем
,
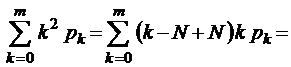
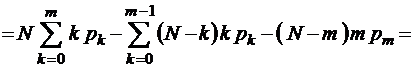
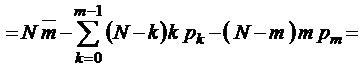
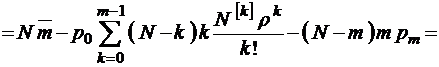
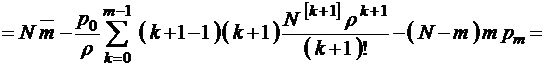
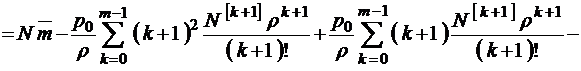
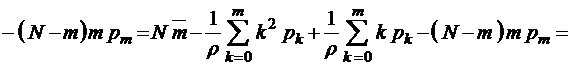
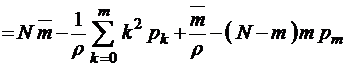откуда
,
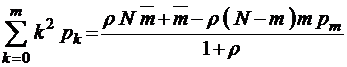и тогда второй центральный момент
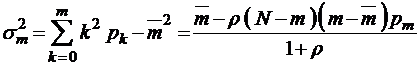. (3.3.6)
При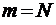 
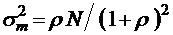в соответствии с результатом (3.2.6). Заметим, что формулу (3.3.6) можно получить, конечно, и по алгоритму, представленному в § 3.2. В этом случае 
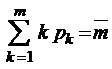, и тогда параметр 
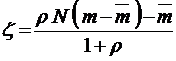, так что
.
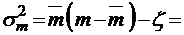
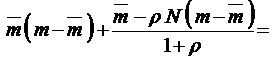
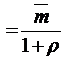
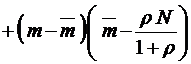Зависимость (3.3.6) получается из этой формулы простой подстановкой во второй сомножитель последнего слагаемого соотношения (3.3.5).
Среднее время обслуживания требования одним каналом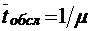 
( 
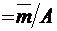), дисперсия времени обслуживания 
.
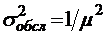Сводка формул
; 
;
; 
;
; 
;
; 
;
; 
; 
; 
;
.
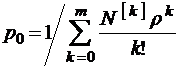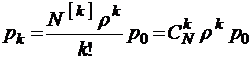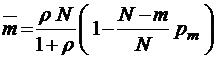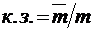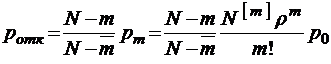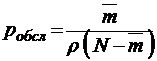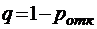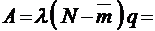
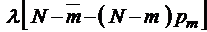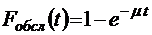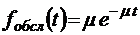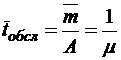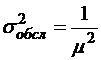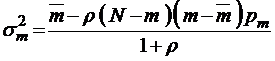Модель М/М/m/Е/N
Рассматриваемая в этом разделе система массового обслуживания является наиболее общей по отношению к трем изученным выше вариантам замкнутых СМО и при соответствующем выборе ее пара-
метров может быть сведена к любому из них. Предположим, что в системе имеется конечное число требований, m обслуживающих приборов (каналов) и, кроме того, конечное число мест для ожидания, что общее число требований в очереди не может превышать E. Предположим также, что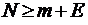 
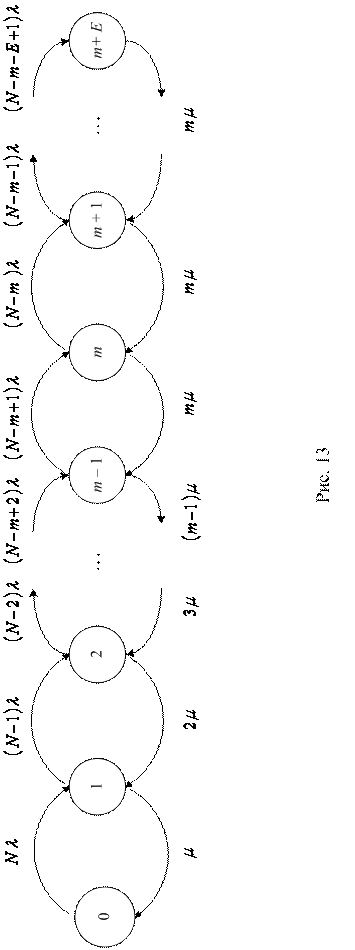
, при этом все требования, поступающие в систему тогда, когда в ней уже имеется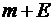 
заявок, теряются и немедленно возвращаются в группу поступающих так, как будто бы они были полностью обслужены (на языке символики Кендалла – это система М/М/m/E/N). Граф состояний такой СМО имеет вид, изображенный на рис. 13. При 
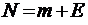эта модель переходит в модель зам-кнутой многоканальной СМО, рассмотренную в § 3.2, а при 
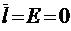в модель Энгсета.
Решение уравнений Колмогорова в данном случае вполне аналогично тому, которое было получено в § 3.2 для модели М/М/m//N, так что запишем сразу его конечный результат, которым является связка формул
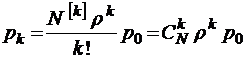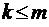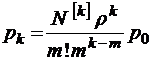при 
;
при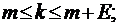 
.
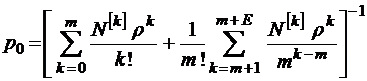