Модели замкнутых систем массового обслуживания
ЧАСТЬ 3.
МОДЕЛИ ЗАМКНУТЫХ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ
Модель М/М/1/N
До сих пор мы рассматривали такие системы массового обслуживания, в которых все заявки приходили откуда-то извне, и при этом интенсивность потока поступающих в систему заявок не зависела от состояния самой системы. Тем самым считалось, что источник располагает неограниченным числом требований. В этом случае поступающий поток заявок (по нашему предположению – пуассоновский) характеризуется как процесс, не зависимый от выходящего потока. Системы массового обслуживания такого рода называют разомкнутыми (или открытыми), считается, что их питает источник, располагающий бесконечным числом заявок.
Рассмотрим теперь тот случай, когда узел обслуживания предназначен для обслуживания конечного (обычно постоянного) числа циркулирующих в системе заявок. В этом случае, как только требования обслуживаются, они возвращаются обратно в источник. Задачи такого рода особенно часто встречаются при эксплуатации машин и механизмов (или комплексного оборудования), которые могут выходить из строя, но восстанавливаются после ремонта. Требования, покидающие систему, при этом возвращаются обратно в источник, где они пребывают в течение некоторого случайного промежутка времени, а затем вновь поступают в систему. Такого рода системы называются замкнутыми системами массового обслуживания.
Еще одним примером таких систем является так называемая сеть массового обслуживания. Источник сети при этом рассматривается как система, в свою очередь, нагружаемая выходами самой сети массового обслуживания. В более общем случае требование последовательно проходит через несколько систем, и тогда мы имеем сеть, структура которой определяется правилами циркуляции требований в различных системах массового обслуживания (такая сеть, конечно, может быть как замкнутой, так и разомкнутой).
В сущности, любая СМО, конечно, имеет дело только с ограниченным числом заявок, но весьма часто число их так велико, что на практике влиянием эффектов, связанных с конечностью числа требований, на функционирование системы можно пренебречь. Например, поток вызовов на АТС крупного города исходит, в сущности, от ограниченного числа абонентов, но это число так велико, что практически его можно считать бесконечным.
Итак, рассмотрим тот случай, когда входящий в систему пуассоновский поток требований создается конечной группой ее возможных клиентов. Систему будем считать состоящей из очереди и одного обслуживающего прибора. Пусть структура системы такова, что всего имеется N >1 заявок (требований), циркулирующих в системе, но при этом каждое требование может либо реально находиться в системе (в очереди или под обслуживанием), либо вне системы (фактически пребывая в источнике), чтобы через некоторое время вновь в нее вернуться. Все заявки поступают в систему и обслуживаются прибором независимо друг от друга. Ясно при этом, что если в системе находится k требований (очередь плюс прибор обслуживания), то в числе поступающих в систему (в источнике) будет находиться 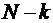 заявок.
заявок.
Пусть интервал времени, через которое каждое требование после его обслуживания и повторного пребывания в источнике заявок, вновь поступает в систему, есть некоторая случайная величина. Будем считать, что эта случайная величина распределена по показательному (экспоненциальному) закону, со средним значением, рав-
ным 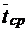 . Или, что то же самое,
. Или, что то же самое, 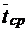 ‑ это среднее время нахождения одного требования в источнике заявок от окончания обслуживания и до его возвращения обратно в систему. В этом случае физический смысл интенсивности
‑ это среднее время нахождения одного требования в источнике заявок от окончания обслуживания и до его возвращения обратно в систему. В этом случае физический смысл интенсивности 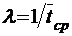 , очевидно, заключается в том, что она определяет среднее число возвращений в единицу времени (своего рода частоту возвращений) одной заявки после обслуживания обратно в систему. И тогда, в свою очередь, общая интенсивность поступающих в систему требований равна
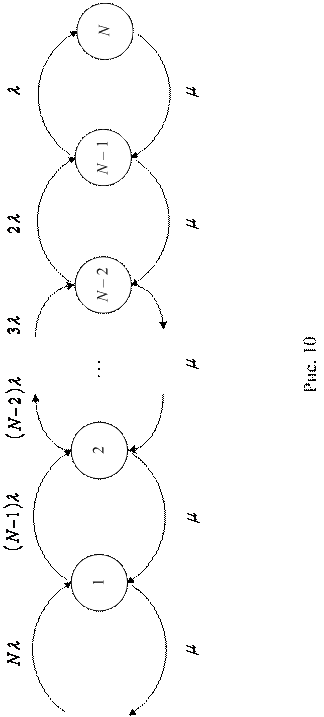
, очевидно, заключается в том, что она определяет среднее число возвращений в единицу времени (своего рода частоту возвращений) одной заявки после обслуживания обратно в систему. И тогда, в свою очередь, общая интенсивность поступающих в систему требований равна 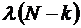 , где k – номер состояния системы, то есть число заявок, реально в ней находящихся, как в очереди, так и под обслуживанием. Граф такой системы изображен на рис. 10. В рамках символики Кендалла такие системы массового обслуживания обозначают аббревиатурой М/М/1//N, в которой последний символ означает полное (предельное) число заявок в системе.
, где k – номер состояния системы, то есть число заявок, реально в ней находящихся, как в очереди, так и под обслуживанием. Граф такой системы изображен на рис. 10. В рамках символики Кендалла такие системы массового обслуживания обозначают аббревиатурой М/М/1//N, в которой последний символ означает полное (предельное) число заявок в системе.
Заметим, что в строгом смысле замкнутые системы массового обслуживания являются саморегулируемыми. В самом деле, если такая система перегружена, вследствие чего в ней образовалась большая очередь ждущих обслуживания заявок, то интенсивность поступающего в систему потока дополнительных требований падает, что предотвращает дальнейший перегруз системы. Говоря другими словами, замкнутые СМО – это СМО с обратной связью.
Применяя общие формулы расчета вероятностей стационарных состояний для процесса гибели и размножения, изображенного на графе состояний (рис. 10), имеем
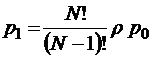 ;
; 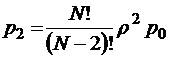 ;
; 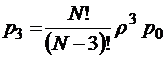 ; …;
; …;
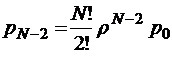 ;
; 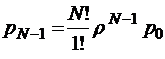 ;
; 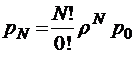 .
.
В общем виде
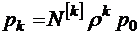
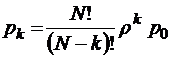 или
или
для всех 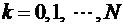 . Здесь
. Здесь
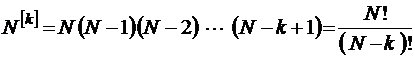 ;
;
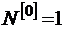 – так называемые факториальные многочлены или обобщенные степени [17]. Ясно, что при этом
– так называемые факториальные многочлены или обобщенные степени [17]. Ясно, что при этом
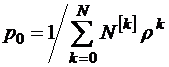 . (3.1.1)
. (3.1.1)
Сводка формул
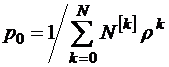 ;
; 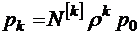 ;
;
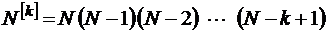 (факториальные многочлены);
(факториальные многочлены);
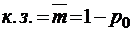 ;
; 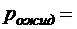
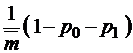 ;
; 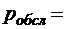
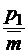 ;
;
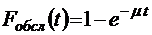 ;
; 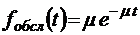 ;
; 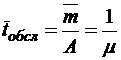 ;
; 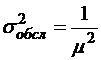 ;
;
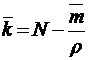 ;
; 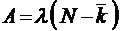 ;
; 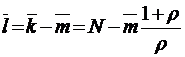 ;
;
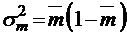 ;
; 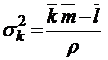 ;
; 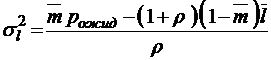 ;
;
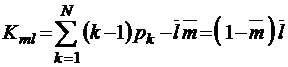 ;
; 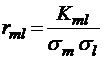 ;
;
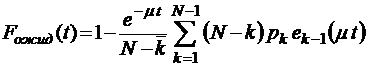 ;
;
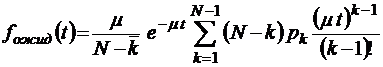 ;
;
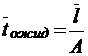 ;
; 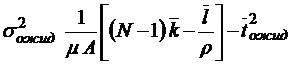 ;
;
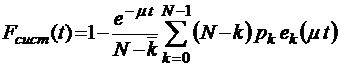 ;
;
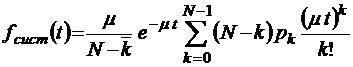 ;
;
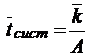 ;
; 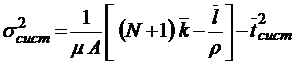 .
.
Модель М/М/m//N
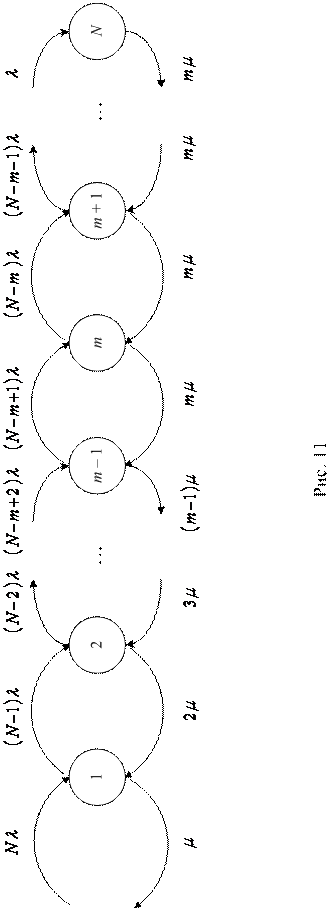
Рассмотрим теперь более общий случай замкнутой СМО, имеющей в наличии m обслуживающих каналов. Все каналы имеют одинаковую интенсивность обслуживания 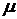 . Точно так же, как и в предыдущем случае, общая интенсивность поступающего в систему потока заявок составляет
. Точно так же, как и в предыдущем случае, общая интенсивность поступающего в систему потока заявок составляет 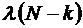 . Очевидно при этом, что если число приборов превышает общее число N требований в системе (или равно ему), то для каждого требования можно выделить свой обслуживающий прибор и, таким образом, требования никогда не будут ожидать обслуживания. При этом приборы, не связанные ни с одним из требований, останутся бездействующими и их можно вообще не учитывать. Таким образом, нам достаточно рассмотреть лишь тот случай, когда
. Очевидно при этом, что если число приборов превышает общее число N требований в системе (или равно ему), то для каждого требования можно выделить свой обслуживающий прибор и, таким образом, требования никогда не будут ожидать обслуживания. При этом приборы, не связанные ни с одним из требований, останутся бездействующими и их можно вообще не учитывать. Таким образом, нам достаточно рассмотреть лишь тот случай, когда 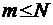 .
.
Граф такой системы имеет вид, изображенный на рис. 11 (на языке символики Кендалла – это система М/М/m//N). Вычисляя вероятности стационарных состояний системы обычным образом, имеем
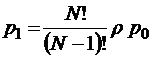 ;
; 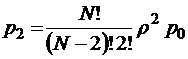 ;
; 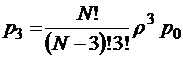 ;
;
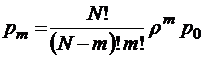 ;
; 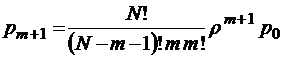 ;
;
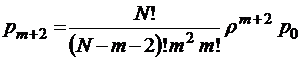 ; … ;
; … ;
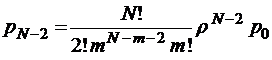 ;
; 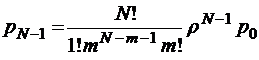 ;
;
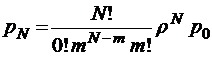 ,
,
так что в общем виде
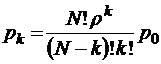 при
при 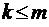 ;
;
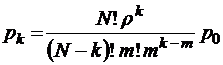 при
при 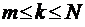
или 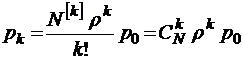 при
при 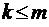 ;
; 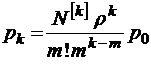 при
при
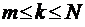 , где
, где 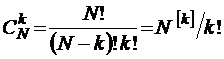 – биномиальные коэффициенты. Ясно, что при этом
– биномиальные коэффициенты. Ясно, что при этом
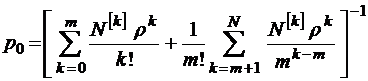 .
.
Для случая 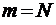 очереди нет, и тогда имеем особенно простую зависимость (формула бинома Ньютона)
очереди нет, и тогда имеем особенно простую зависимость (формула бинома Ньютона)
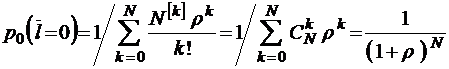 .
.
Сводка формул
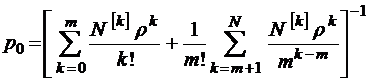 ;
;
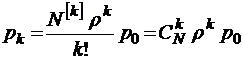 при
при 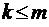 ;
;
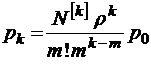 при
при 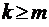 ;
;
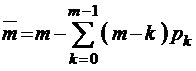 ;
; 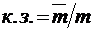 ;
;
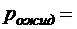
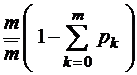 ;
; 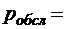
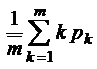 ;
;
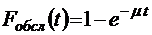 ;
; 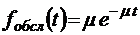 ;
; 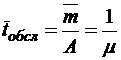 ;
; 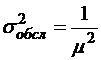 ;
;
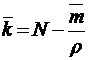 ;
; 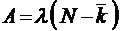 ;
; 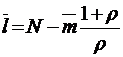
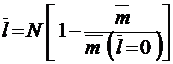 ;
;
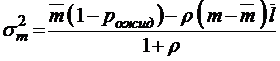 ;
; 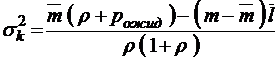 ;
;
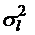
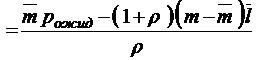 ;
;
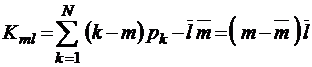 ;
; 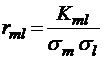 ;
;
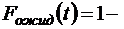
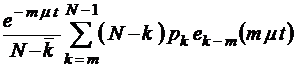 ;
;
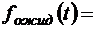
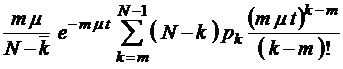 ;
;
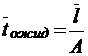 ;
; 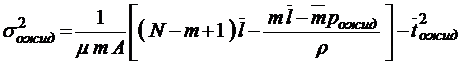 ;
;
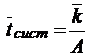 ;
;
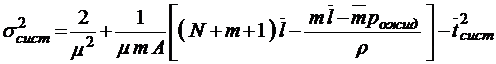 .
.
При 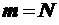
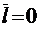 ;
; 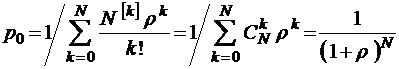 ;
;
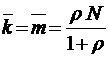 ;
; 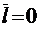 ;
; 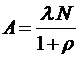 ;
; 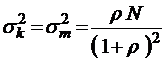 ;
;
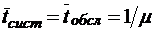 ;
; 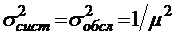 .
.
Сводка формул
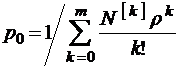 ;
; 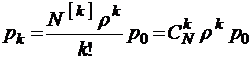 ;
;
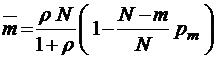 ;
; 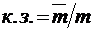 ;
;
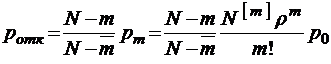 ;
; 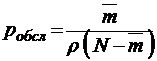 ;
;
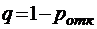 ;
; 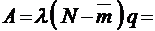
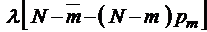 ;
;
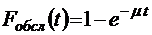 ;
; 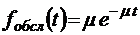 ;
; 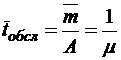 ;
; 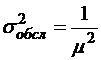 ;
;
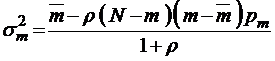 .
.
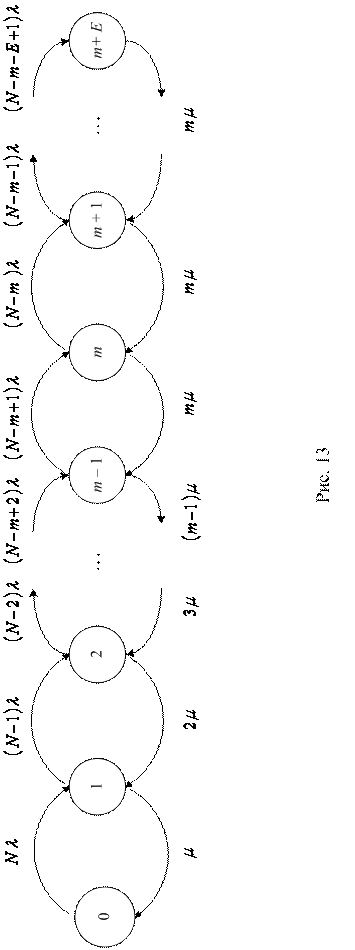
Модель М/М/m/Е/N
Рассматриваемая в этом разделе система массового обслуживания является наиболее общей по отношению к трем изученным выше вариантам замкнутых СМО и при соответствующем выборе ее пара-
метров может быть сведена к любому из них. Предположим, что в системе имеется конечное число требований, m обслуживающих приборов (каналов) и, кроме того, конечное число мест для ожидания, что общее число требований в очереди не может превышать E. Предположим также, что 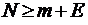 , при этом все требования, поступающие в систему тогда, когда в ней уже имеется
, при этом все требования, поступающие в систему тогда, когда в ней уже имеется 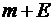 заявок, теряются и немедленно возвращаются в группу поступающих так, как будто бы они были полностью обслужены (на языке символики Кендалла – это система М/М/m/E/N). Граф состояний такой СМО имеет вид, изображенный на рис. 13. При
заявок, теряются и немедленно возвращаются в группу поступающих так, как будто бы они были полностью обслужены (на языке символики Кендалла – это система М/М/m/E/N). Граф состояний такой СМО имеет вид, изображенный на рис. 13. При 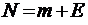 эта модель переходит в модель зам-кнутой многоканальной СМО, рассмотренную в § 3.2, а при
эта модель переходит в модель зам-кнутой многоканальной СМО, рассмотренную в § 3.2, а при 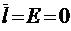 в модель Энгсета.
в модель Энгсета.
Решение уравнений Колмогорова в данном случае вполне аналогично тому, которое было получено в § 3.2 для модели М/М/m//N, так что запишем сразу его конечный результат, которым является связка формул
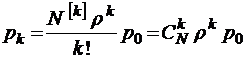 при
при 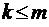 ;
;
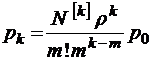 при
при 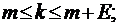
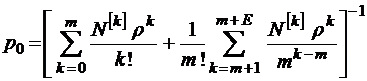 .
.
Сводка формул
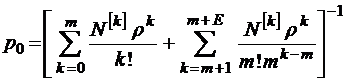 ;
;
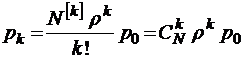 при
при 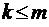 ;
;
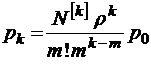 при
при 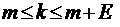 ;
;
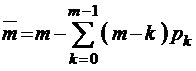 ;
; 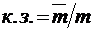 ;
;
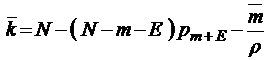 ;
; 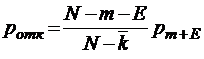 ;
;
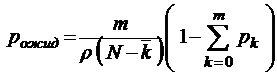 ;
; 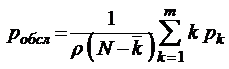 ;
;
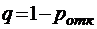 ;
; 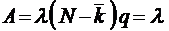
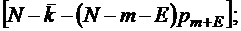
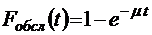 ;
; 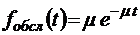 ;
; 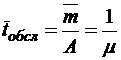 ;
; 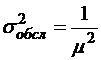 ;
;
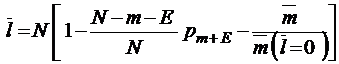 ;
; 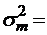
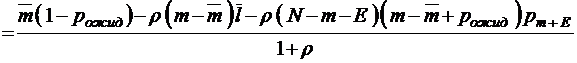 ;
;
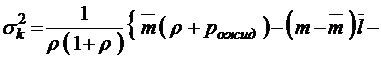
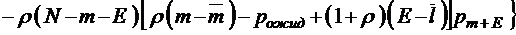 ;
;
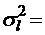
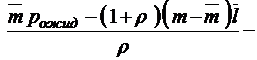
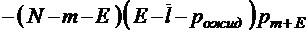 ;
;
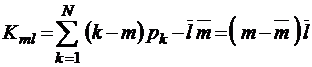 ;
; 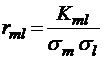 ;
;
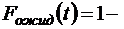
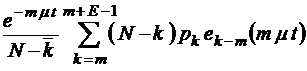 ;
;
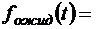
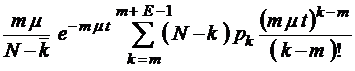 ;
;
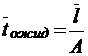 ;
; 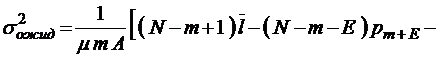
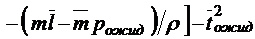 ;
; 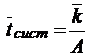 ;
;
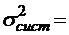
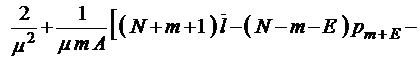
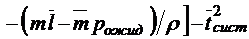 ;
;
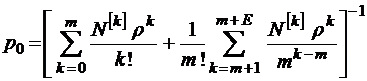 .
.
Сводка формул
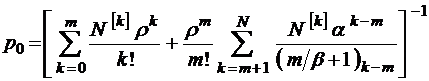 ;
;
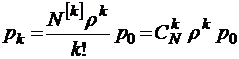 при
при 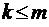 ;
;
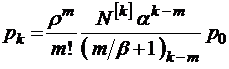 при
при 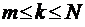 ;
;
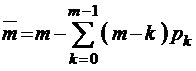 ;
; 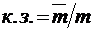 ;
;
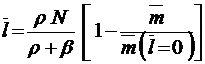 ;
;
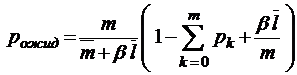 ;
; 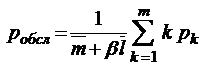 ;
;
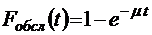 ;
; 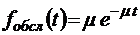 ;
; 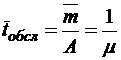 ;
; 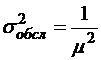 ;
;
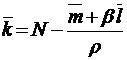 ;
; 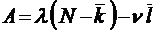 ;
; 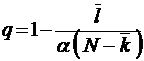 ;
;
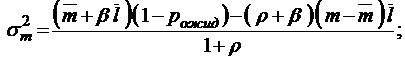
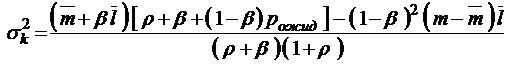 ;
;
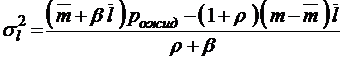 ;
;
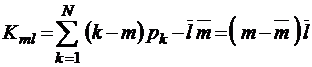 ;
; 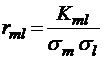 ;
;
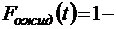
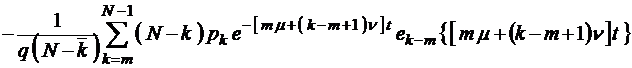 ;
;
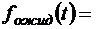
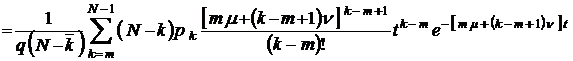 ;
;
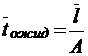 ;
; 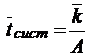 ;
;
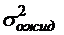
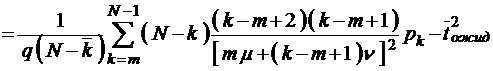 ;
;
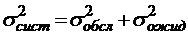 .
.
Эта систему формул так же, как и в случае открытых систем массового обслуживания, можно распространить и на системы с ограниченным средним временем пребывания в системе в целом (то есть как в очереди, так и в обслуживающем приборе), если в ней всюду совершить ту же замену 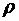 на
на 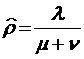 и
и 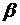 на
на 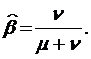
ЧАСТЬ 3.
МОДЕЛИ ЗАМКНУТЫХ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ
Модель М/М/1/N
До сих пор мы рассматривали такие системы массового обслуживания, в которых все заявки приходили откуда-то извне, и при этом интенсивность потока поступающих в систему заявок не зависела от состояния самой системы. Тем самым считалось, что источник располагает неограниченным числом требований. В этом случае поступающий поток заявок (по нашему предположению – пуассоновский) характеризуется как процесс, не зависимый от выходящего потока. Системы массового обслуживания такого рода называют разомкнутыми (или открытыми), считается, что их питает источник, располагающий бесконечным числом заявок.
Рассмотрим теперь тот случай, когда узел обслуживания предназначен для обслуживания конечного (обычно постоянного) числа циркулирующих в системе заявок. В этом случае, как только требования обслуживаются, они возвращаются обратно в источник. Задачи такого рода особенно часто встречаются при эксплуатации машин и механизмов (или комплексного оборудования), которые могут выходить из строя, но восстанавливаются после ремонта. Требования, покидающие систему, при этом возвращаются обратно в источник, где они пребывают в течение некоторого случайного промежутка времени, а затем вновь поступают в систему. Такого рода системы называются замкнутыми системами массового обслуживания.
Еще одним примером таких систем является так называемая сеть массового обслуживания. Источник сети при этом рассматривается как система, в свою очередь, нагружаемая выходами самой сети массового обслуживания. В более общем случае требование последовательно проходит через несколько систем, и тогда мы имеем сеть, структура которой определяется правилами циркуляции требований в различных системах массового обслуживания (такая сеть, конечно, может быть как замкнутой, так и разомкнутой).
В сущности, любая СМО, конечно, имеет дело только с ограниченным числом заявок, но весьма часто число их так велико, что на практике влиянием эффектов, связанных с конечностью числа требований, на функционирование системы можно пренебречь. Например, поток вызовов на АТС крупного города исходит, в сущности, от ограниченного числа абонентов, но это число так велико, что практически его можно считать бесконечным.
Итак, рассмотрим тот случай, когда входящий в систему пуассоновский поток требований создается конечной группой ее возможных клиентов. Систему будем считать состоящей из очереди и одного обслуживающего прибора. Пусть структура системы такова, что всего имеется N >1 заявок (требований), циркулирующих в системе, но при этом каждое требование может либо реально находиться в системе (в очереди или под обслуживанием), либо вне системы (фактически пребывая в источнике), чтобы через некоторое время вновь в нее вернуться. Все заявки поступают в систему и обслуживаются прибором независимо друг от друга. Ясно при этом, что если в системе находится k требований (очередь плюс прибор обслуживания), то в числе поступающих в систему (в источнике) будет находиться 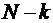 заявок.
заявок.
Пусть интервал времени, через которое каждое требование после его обслуживания и повторного пребывания в источнике заявок, вновь поступает в систему, есть некоторая случайная величина. Будем считать, что эта случайная величина распределена по показательному (экспоненциальному) закону, со средним значением, рав-
ным 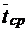 . Или, что то же самое,
. Или, что то же самое, 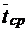 ‑ это среднее время нахождения одного требования в источнике заявок от окончания обслуживания и до его возвращения обратно в систему. В этом случае физический смысл интенсивности
‑ это среднее время нахождения одного требования в источнике заявок от окончания обслуживания и до его возвращения обратно в систему. В этом случае физический смысл интенсивности 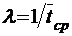 , очевидно, заключается в том, что она определяет среднее число возвращений в единицу времени (своего рода частоту возвращений) одной заявки после обслуживания обратно в систему. И тогда, в свою очередь, общая интенсивность поступающих в систему требований равна
, очевидно, заключается в том, что она определяет среднее число возвращений в единицу времени (своего рода частоту возвращений) одной заявки после обслуживания обратно в систему. И тогда, в свою очередь, общая интенсивность поступающих в систему требований равна 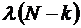 , где k – номер состояния системы, то есть число заявок, реально в ней находящихся, как в очереди, так и под обслуживанием. Граф такой системы изображен на рис. 10. В рамках символики Кендалла такие системы массового обслуживания обозначают аббревиатурой М/М/1//N, в которой последний символ означает полное (предельное) число заявок в системе.
, где k – номер состояния системы, то есть число заявок, реально в ней находящихся, как в очереди, так и под обслуживанием. Граф такой системы изображен на рис. 10. В рамках символики Кендалла такие системы массового обслуживания обозначают аббревиатурой М/М/1//N, в которой последний символ означает полное (предельное) число заявок в системе.
Заметим, что в строгом смысле замкнутые системы массового обслуживания являются саморегулируемыми. В самом деле, если такая система перегружена, вследствие чего в ней образовалась большая очередь ждущих обслуживания заявок, то интенсивность поступающего в систему потока дополнительных требований падает, что предотвращает дальнейший перегруз системы. Говоря другими словами, замкнутые СМО – это СМО с обратной связью.
Применяя общие формулы расчета вероятностей стационарных состояний для процесса гибели и размножения, изображенного на графе состояний (рис. 10), имеем
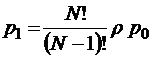 ;
; 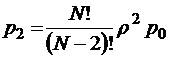 ;
; 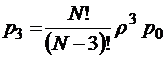 ; …;
; …;
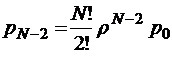 ;
; 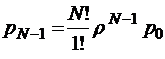 ;
; 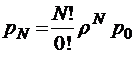 .
.
В общем виде

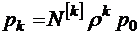
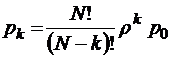 или
или
для всех 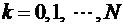 . Здесь
. Здесь
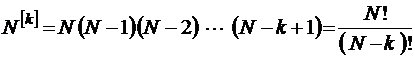 ;
;
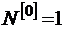 – так называемые факториальные многочлены или обобщенные степени [17]. Ясно, что при этом
– так называемые факториальные многочлены или обобщенные степени [17]. Ясно, что при этом
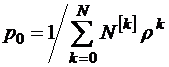 . (3.1.1)
. (3.1.1)
