Математические модели с использованием систем массового обслуживания
Эти системы основаны на марковском случайном процессе. Физическая система 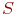 с течением времени меняет свое состояние (переходит из одного состояния в другое) случайным образом. Тогда в системе
с течением времени меняет свое состояние (переходит из одного состояния в другое) случайным образом. Тогда в системе 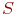 протекает случайный процесс, который называется марковским, если для любого момента времени
протекает случайный процесс, который называется марковским, если для любого момента времени 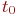 вероятностные характеристики процесса в "будущем" зависят только от его состояния в данный момент времени
вероятностные характеристики процесса в "будущем" зависят только от его состояния в данный момент времени 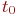 и не зависят от того, когда и как система пришла в это состояние. Вероятностные характеристики в "будущем" можно найти: например, вероятность того, что через некоторое время т система
и не зависят от того, когда и как система пришла в это состояние. Вероятностные характеристики в "будущем" можно найти: например, вероятность того, что через некоторое время т система 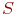 окажется в состоянии
окажется в состоянии 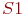 или сохранит состояние
или сохранит состояние 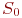 , и т. д.
, и т. д.
Таким образом, в марковском случайном процессе "будущее" зависит от "прошлого" только через "настоящее".
Рассматривая марковские процессы с дискретными состояниями и непрерывным временем, удобно будет представлять, что все переходы системы 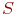 из состояния в состояние происходят под действием каких-то потоков событий (поток вызовов, отказов, восстановлений и т. п.). Если все потоки событий, переводящие систему
из состояния в состояние происходят под действием каких-то потоков событий (поток вызовов, отказов, восстановлений и т. п.). Если все потоки событий, переводящие систему 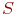 из состояния в состояние, - простейшие, то процесс, протекающий в системе, будет марковским. Это и естественно, так как простейший поток не обладает последействием: в нем "будущее" не зависит от "прошлого".
из состояния в состояние, - простейшие, то процесс, протекающий в системе, будет марковским. Это и естественно, так как простейший поток не обладает последействием: в нем "будущее" не зависит от "прошлого".
Если система S находится в каком-то состоянии 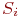 , из которого есть непосредственный переход в другое состояние
, из которого есть непосредственный переход в другое состояние 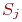 (стрелка, ведущая из
(стрелка, ведущая из 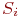 в
в 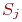 на графе состояний), то это можно представлять так, как будто на систему, пока она находится в состоянии
на графе состояний), то это можно представлять так, как будто на систему, пока она находится в состоянии 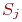 , действует простейший поток событий, приводящий ее по стрелке
, действует простейший поток событий, приводящий ее по стрелке  . Как только появится первое событие этого потока, происходит "перескок" системы из
. Как только появится первое событие этого потока, происходит "перескок" системы из 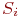 в
в 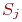 .
.
Для наглядности очень удобно представлять граф состояний. Построим размеченный граф состояний для технического устройства из двух узлов. Состояния системы будут:
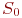 - оба узла исправны;
- оба узла исправны;
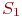 - первый узел ремонтируется, второй исправен;
- первый узел ремонтируется, второй исправен;
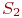 - второй узел ремонтируется, первый исправен;
- второй узел ремонтируется, первый исправен;
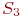 - оба узла ремонтируются.
- оба узла ремонтируются.
Интенсивность потоков событий, переводящих систему из состояния в состояние, вычисляется при условии, что среднее время ремонта узла не зависит от того, ремонтируется ли один узел или оба сразу. Это будет именно так, если ремонтом каждого узла занят отдельный специалист. Найдем все интенсивности потоков событий, переводящих систему из состояния в состояние. Пусть система находится в состоянии 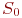 . Какой поток событий переводит ее в состояние
. Какой поток событий переводит ее в состояние 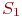 ? Очевидно, поток отказов первого узла. Его интенсивность
? Очевидно, поток отказов первого узла. Его интенсивность 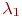 равна единице, деленной на среднее время безотказной работы первого узла. Какой поток событий переводит систему обратно из
равна единице, деленной на среднее время безотказной работы первого узла. Какой поток событий переводит систему обратно из 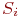 в
в 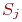 ? Очевидно, поток "окончаний ремонтов" первого узла. Его интенсивность
? Очевидно, поток "окончаний ремонтов" первого узла. Его интенсивность 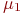 равна единице, деленной на среднее время ремонта первого узла. Аналогично вычисляются интенсивности потоков событий, переводящих систему по всем стрелкам графа рис. 13.2.
равна единице, деленной на среднее время ремонта первого узла. Аналогично вычисляются интенсивности потоков событий, переводящих систему по всем стрелкам графа рис. 13.2.
Имея в своем распоряжении размеченный граф состояний системы, легко построить математическую модель данного процесса.
В самом деле, пусть рассматривается система 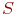 , имеющая
, имеющая 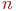 возможных состояний
возможных состояний 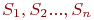 . Назовем вероятностью i-го состояния вероятность
. Назовем вероятностью i-го состояния вероятность 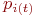 того, что в момент
того, что в момент 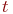 система будет находиться в состоянии
система будет находиться в состоянии 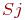 . Очевидно, что для любого момента сумма всех вероятностей состояний равна единице:
. Очевидно, что для любого момента сумма всех вероятностей состояний равна единице:
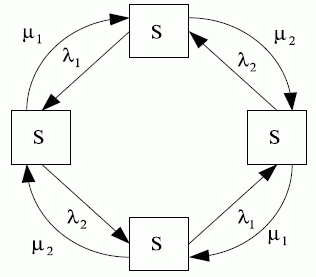
Рис. 13.2. Размеченный граф
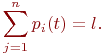 | (13.6) |
Имея в своем распоряжении размеченный граф состояний, можно найти все вероятности состояний 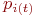 как функции времени. Для этого составляют и решают так называемые уравнения Колмогорова - особый вид дифференциальных уравнений, в которых неизвестными функциями являются вероятности состояний.
как функции времени. Для этого составляют и решают так называемые уравнения Колмогорова - особый вид дифференциальных уравнений, в которых неизвестными функциями являются вероятности состояний.
Рассматривается методика использования основных понятий теории множеств при решении задач конструкторского проектирования. Содержание
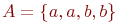 не является множеством. Существует два основных способа задания множеств: перечисление и описание. Первый способ состоит в том, что задаётся и перечисляется полный список элементов, входящих в множество. Например, множество элементов схемы РЭС определяется их списком. Данный способ удобно применять только к ограниченному числу конечных множеств. Второй способ применяется, когда множество нельзя или затруднительно задать с помощью списка (это может относиться к конечным и бесконечным множествам). В таком случае множества определяются свойствами их элементов. Множество не является множеством. Существует два основных способа задания множеств: перечисление и описание. Первый способ состоит в том, что задаётся и перечисляется полный список элементов, входящих в множество. Например, множество элементов схемы РЭС определяется их списком. Данный способ удобно применять только к ограниченному числу конечных множеств. Второй способ применяется, когда множество нельзя или затруднительно задать с помощью списка (это может относиться к конечным и бесконечным множествам). В таком случае множества определяются свойствами их элементов. Множество 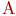 считается заданным, если указано свойство считается заданным, если указано свойство 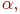 которым обладают все элементы, принадлежащие множеству А, и которым элементы, не принадлежащие множеству которым обладают все элементы, принадлежащие множеству А, и которым элементы, не принадлежащие множеству 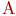 , не обладают. Если , не обладают. Если 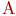 - произвольное множество, а - произвольное множество, а 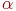 - некоторое свойство, то запись - некоторое свойство, то запись 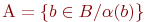 означает множество тех и только тех элементов означает множество тех и только тех элементов 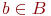 , которые обладают свойством , которые обладают свойством 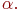 При задании множеств вторым способом необходимо так задавать свойство, характеризующее элементы множества, чтобы оно было общим непротиворечивым для всех его элементов. Как основное понятие теории, понятие множества не подлежит логическому определению. Элементы множества могут иметь различную природу. Например, можно говорить о множестве микросхем, входящих в определённую конструкцию РЭС, или о множестве чертежей, входящих в полный комплект конструкторской документации для производства какого-либо изделия. Множества обозначают заглавными буквами латинского алфавита: При задании множеств вторым способом необходимо так задавать свойство, характеризующее элементы множества, чтобы оно было общим непротиворечивым для всех его элементов. Как основное понятие теории, понятие множества не подлежит логическому определению. Элементы множества могут иметь различную природу. Например, можно говорить о множестве микросхем, входящих в определённую конструкцию РЭС, или о множестве чертежей, входящих в полный комплект конструкторской документации для производства какого-либо изделия. Множества обозначают заглавными буквами латинского алфавита: 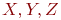 и т.д., а элементы множества - соответствующими строчными буквами того же алфавита: и т.д., а элементы множества - соответствующими строчными буквами того же алфавита: 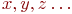 или строчными буквами с индексами: или строчными буквами с индексами: 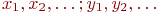 и т.д. Равенство и т.д. Равенство 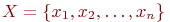 свидетельствует о том, что элементы свидетельствует о том, что элементы 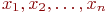 являются элементами множества являются элементами множества  . Множество можно задавать не только перечислением его элементов, но и с помощью описательного способа, указывающего характерное свойство, которым обладают все элементы этого множества. Например, если во всём множестве . Множество можно задавать не только перечислением его элементов, но и с помощью описательного способа, указывающего характерное свойство, которым обладают все элементы этого множества. Например, если во всём множестве  микросхем электронного блока сложной радиоаппаратуры есть некоторое множество микросхем электронного блока сложной радиоаппаратуры есть некоторое множество 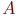 гибридных интегральных схем, то это можно записать так: гибридных интегральных схем, то это можно записать так: 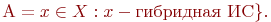 Это читается так: множество Это читается так: множество 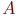 состоит из элементов состоит из элементов 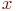 множества множества  , обладающих тем свойством, что , обладающих тем свойством, что 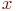 является гибридной интегральной схемой. Здесь введено новое обозначение является гибридной интегральной схемой. Здесь введено новое обозначение 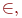 означающее, что объект означающее, что объект 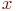 является элементом множества является элементом множества  . Если же некоторый объект . Если же некоторый объект 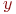 не принадлежит множеству не принадлежит множеству  , то это условие записывают в виде , то это условие записывают в виде 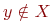 . В том случае, когда не вызывает сомнения, из какого множества берутся элементы . В том случае, когда не вызывает сомнения, из какого множества берутся элементы 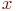 , принадлежность их к множеству , принадлежность их к множеству  можно не указывать. Например, известно, что множество гибридных интегральных схем входит во множество микросхем того же самого электронного блока, тогда запись будет иметь вид можно не указывать. Например, известно, что множество гибридных интегральных схем входит во множество микросхем того же самого электронного блока, тогда запись будет иметь вид  Число элементов множества Число элементов множества 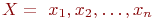 называют мощностью этого множества и обозначают прямыми скобками, например, называют мощностью этого множества и обозначают прямыми скобками, например, 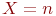 . Если число элементов множества . Если число элементов множества  конечно, то такое множество называют конечным.В противном случае множество будет бесконечным. В теории множеств вводится понятие пустого множества, в котором не содержится ни одного элемента. Пустое множество обозначают специальным символом конечно, то такое множество называют конечным.В противном случае множество будет бесконечным. В теории множеств вводится понятие пустого множества, в котором не содержится ни одного элемента. Пустое множество обозначают специальным символом 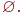 Например, если множество Например, если множество  пусто, то пишут пусто, то пишут 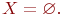 Последовательность из Последовательность из 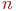 элементов множества называют n - строкой. В отличие от обычного множества, где порядок элементов безразличен, в элементов множества называют n - строкой. В отличие от обычного множества, где порядок элементов безразличен, в 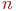 - строке обязательно задаётся их определённая последовательность. Множество - строке обязательно задаётся их определённая последовательность. Множество  равно множеству равно множеству 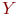 , если оба эти множества состоят из одних и тех же элементов. Если множество , если оба эти множества состоят из одних и тех же элементов. Если множество  полностью содержится во множестве полностью содержится во множестве 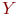 и при этом и при этом 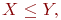 то говорят, что множество то говорят, что множество  является подмножеством множества Y: является подмножеством множества Y: 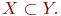 Следовательно, мы рассмотрели два соотношения: - принадлежность Следовательно, мы рассмотрели два соотношения: - принадлежность 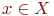 ; - включение ; - включение 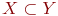 . Первое определяет связь между множеством и его элементами, а второе - между двумя множествами. В случае, когда . Первое определяет связь между множеством и его элементами, а второе - между двумя множествами. В случае, когда 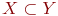 и, одновременно, и, одновременно, 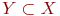 , имеет место равенство , имеет место равенство 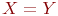 , т.е. множества , т.е. множества  и и 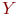 совпадают. Символическая запись совпадают. Символическая запись 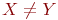 означает, что множество означает, что множество  не совпадает с множеством не совпадает с множеством 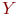 . . |
 |
Лекция: Математические методы описания моделей конструкций РЭС. Элементы теории графов

С использованием введенных в предыдущей лекции элементов теории множеств рассматриваются элементы теории графов при решении задач конструкторского проектирования.
Содержание
- 17.1. Основные понятия
- 17. 2. Части графа
- 17. 3. Способы задания графов
- Матрица смежности
- Матрица весовых соотношений
- Матрица инцидентности
- Контрольные вопросы
Изложить основные понятия теории графов, знание которых является обязательным при современном конструкторском проектировании РЭС.
Основные понятия
Теорию графов применяют для решения таких задач, как анализ электронных схем, разбиение и размещение электронных элементов, проектирование проводного и печатного монтажа, сетевое планирование и многих других. Это объясняется тем, что использование графов сокращает объём вычислений по сравнению с другими методами и, сохраняя наглядность описания объектов (конструкций), позволяет строить компактные и удобные для реализации на ЭВМ алгоритмы преобразований и оптимизации.
Понятие графа 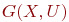 опирается на понятие множества.
опирается на понятие множества.
Под абстрактным графом или просто графом G(X,U) понимают совокупность непустого множества  и изолированного от него подмножества
и изолированного от него подмножества 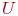 (возможно, пустого), представляющего собой множество всех упорядоченных пар
(возможно, пустого), представляющего собой множество всех упорядоченных пар 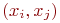 , где
, где 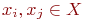 . Элементы множеств
. Элементы множеств  и
и 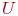 называют, соответственно, вершинами и дугами графа. Следовательно, граф - это множество
называют, соответственно, вершинами и дугами графа. Следовательно, граф - это множество  всех вершин
всех вершин  , связи между которыми определены множеством рёбер
, связи между которыми определены множеством рёбер 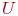 .
.
Геометрически граф можно представить в виде множества точек 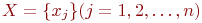 в
в 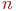 -мерном евклидовом пространстве
-мерном евклидовом пространстве 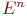 и множества простых, направленных самонепересекающихся кривых
и множества простых, направленных самонепересекающихся кривых
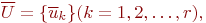
соединяющих 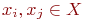 , которые находятся в некотором отношении друг к другу.
, которые находятся в некотором отношении друг к другу.
То, что элемент 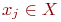 находится в отношении
находится в отношении 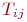 к элементу
к элементу 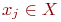 , отображается на графе соединением элементов
, отображается на графе соединением элементов  и
и 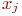 линией со стрелкой в направлении от
линией со стрелкой в направлении от  к
к 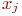 . Такие соединения вершин графа с указанием направления называют ориентированными рёбрами или дугами и записывают так:
. Такие соединения вершин графа с указанием направления называют ориентированными рёбрами или дугами и записывают так:
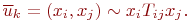
Граф, в котором все вершины соединены дугами, называют ориентированным, направленным или несимметрическим графом.
Аналитически любой ориентированный граф описывается системой алгебраических уравнений, связывающих параметры 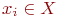 , и наоборот, любая система алгебраических уравнений может быть представлена в виде направленного графа.
, и наоборот, любая система алгебраических уравнений может быть представлена в виде направленного графа.
Пример. Рассмотрим граф, показанный на рис. 17.1.
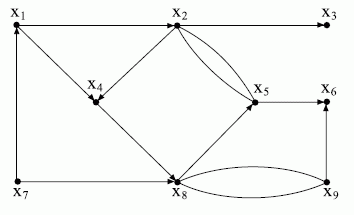
Рис. 17.1. Ориентированный граф
Этот граф определяет следующую систему уравнений:
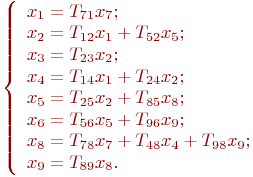
Граф, в котором для любых двух вершин 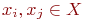 справедливо выражение
справедливо выражение 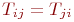 , называют неориентированным, ненаправленным или симметрическим графом.
, называют неориентированным, ненаправленным или симметрическим графом.
В таком графе вершины  и
и 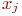 соединены ненаправленной кривой, называемой неориентированным ребром или просто ребром графа (рис. 17.2).
соединены ненаправленной кривой, называемой неориентированным ребром или просто ребром графа (рис. 17.2).
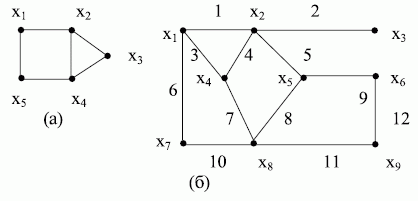
Рис. 17.2. Неориентированные графы
В дальнейшем рассматриваются в основном неориентированные графы, т.к. при решении большинства задач конструкторского проектирования существенным является лишь наличие или отсутствие связей между отдельными элементами конструкции.
При анализе электронных схем, наоборот, пользуются только направленными графами.
На рис. 17.2 неориентированные рёбра обозначены цифрами  .и т.д.
.и т.д.
Две вершины  считаются смежными, если они определяют ребро ( дугу ) и, соответственно, два различных ребра ( дуги ) смежны, если они имеют общую вершину.
считаются смежными, если они определяют ребро ( дугу ) и, соответственно, два различных ребра ( дуги ) смежны, если они имеют общую вершину.
Иными словами, вершина  смежна
смежна  , если
, если 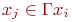 , где
, где 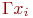 - отображение
- отображение  на множестве
на множестве  .
.
В связи с тем, что отображение 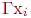 представляет собой совокупность всех вершин графа
представляет собой совокупность всех вершин графа 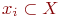 , смежных
, смежных 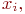 получаем ещё один способ задания графа:
получаем ещё один способ задания графа:
Граф задан, если задано непустое множество 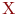 и отображение
и отображение 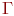 множества
множества 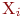 в
в 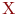 . Обозначим его
. Обозначим его 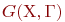 . При геометрической реализации такого графа каждую вершину
. При геометрической реализации такого графа каждую вершину 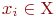 соединяют со всеми вершинами
соединяют со всеми вершинами 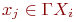 .
.
Например, для графа 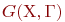 (рис. 17.2,б) можно записать:
(рис. 17.2,б) можно записать:
 | (.\) |
Для графа
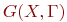
(рис. 17.2, а) запись будет следующей:
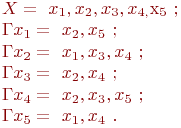
Вершина  инцидента ребру ( дуге )
инцидента ребру ( дуге ) 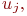 если она является началом или концом ребра ( дуги ). Аналогично утверждение, что ребро ( дуга )
если она является началом или концом ребра ( дуги ). Аналогично утверждение, что ребро ( дуга ) 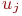 инцидентно вершине
инцидентно вершине  , если оно входит или выходит из этой вершины.
, если оно входит или выходит из этой вершины.
Число рёбер ( дуг ), инцидентных некоторой вершине  , называют локальной степенью вершины и обозначают
, называют локальной степенью вершины и обозначают 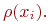
Для графа (рис. 17.2, б) можно записать:
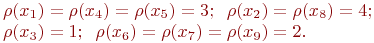
Учитывая, что каждое ребро неориентированного графа инцидентно двум вершинам, получим выражение, связывающее число рёбер графа со степенями вершин
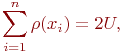 | (U() |
где 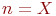 - число вершин графа;
- число вершин графа;
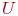 - число рёбер графа.
- число рёбер графа.
Из этого выражения следует, что число вершин с нечётной степенью в графе чётное, так как при опускании всех вершин  с чётными степенями
с чётными степенями 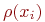 сумма слева остаётся чётной.
сумма слева остаётся чётной.
Вершину, неинцидентную никакому ребру ( дуге ), называют изолированной.
Граф, состоящий только из изолированных вершин ( 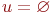 ), называют нуль - графом и обозначают
), называют нуль - графом и обозначают 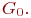
При использовании графов для анализа радиоэлектронных устройств в отдельных случаях целесообразно введение связи вершины самой с собой, т.е.
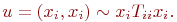
Такую связь называют петлёй.
Если граф 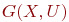 имеет петлю при вершине
имеет петлю при вершине 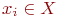 , то
, то 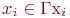 .
.
Отсюда следует, что необходимым и достаточным условием отсутствия петель в графе является
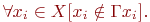
При геометрической реализации графа петля представляется замкнутой дугой, начинающейся и оканчивающейся в одной и той же вершине

и не проходящей через другие вершины графа. Поскольку концевые точки петли совпадают, то петлю считают неориентированной.
Граф называют конечным,если число его рёбер конечно и бесконечным, если число его рёбер бесконечно.
Граф называют однородным степени t, если степени всех его вершин равны t , т.е.



Лекция: Характеристические числа графов и их применение в конструкторском проектировании РЭС

Рассматриваются некоторые характеристические числа графа, позволяющие в ряде случаев упростить решение задач исследования топологических свойств графа.
Содержание
- 18. 1. Цикломатическое число
- 18. 2. Хроматическое число
- 18.3. Плоские графы
- Критерии планарности графов
- Разбиение графа на плоские суграфы
- 18.4. Представление конструкции РЭС с помощью графов
- Контрольные вопросы
Изложить основные понятия теории графов, знание которых является обязательным при современном конструкторском проектировании РЭС.
Рассмотрим некоторые характеристические числа графа, позволяющие в ряде случаев упростить решение задач исследования топологических свойств графа. К таким числам, не зависящим от изоморфных преобразований, относятся: цикломатическое 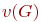 и хроматическое
и хроматическое 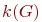 числа, числа внутренней
числа, числа внутренней 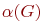 и внешней
и внешней 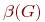 устойчивости графа.
устойчивости графа.
Цикломатическое число
При рассмотрении произвольного неориентированного графа 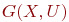 без петель с
без петель с 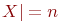 и
и 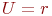 , состоящего из "
, состоящего из " 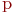 " компонент связности, величину
" компонент связности, величину
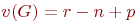 | (18.1) |
называют цикломатическим числом графа.
Иногда вводят понятие ранга графа
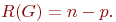 | (18.2) |
В этом случае цикломатическое число
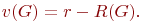 | (18.3) |
Цикломатическое число графа указывает то наименьшее число рёбер, которое нужно удалить из данного графа, чтобы получить дерево (для связного графа) или лес (для несвязного графа), т.е. добиться отсутствия у графа циклов.
Цикломатическое число всегда неотрицательно.
Основное свойство цикломатического числа формулируется в виде теоремы:
Цикломатическое число мультиграфа равно максимальному числу независимых циклов.
Знание цикломатического числа оказывается полезным при анализе топологии электронных схем, а также для решения целого класса задач конструкторского проектирования РЭС.
Пример. Если рассматривать конструкцию печатной платы, то схему электрических соединений можно интерпретировать графом 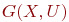 , где
, где  - множество областей контактных площадок, внутри которых проведение проводников запрещено, a
- множество областей контактных площадок, внутри которых проведение проводников запрещено, a 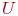 - множество трасс.
- множество трасс.
При этом всё коммутационное пространство разбивается проведёнными соединениями на отдельные, локально замкнутые области
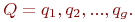 | (18.4) |
Любые две вершины 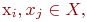 находящиеся в различных областях
находящиеся в различных областях 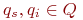 , не могут быть соединены ребром
, не могут быть соединены ребром 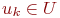 без пересечения рёбер (соединений), ограничивающих области
без пересечения рёбер (соединений), ограничивающих области 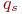 и
и 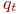 .
.
В связи с этим возникает необходимость контроля непопадания смежных вершин в различные изолированные области.
Цикломатическое число 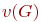 позволяет определить число таких локально замкнутых областей и перейти к решению задачи рационального перераспределения рёбер графа
позволяет определить число таких локально замкнутых областей и перейти к решению задачи рационального перераспределения рёбер графа 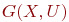 .
.
Хроматическое число
Пусть, задан граф 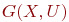 без петель. Разобьём множество его вершин на k непересекающихся подмножеств
без петель. Разобьём множество его вершин на k непересекающихся подмножеств
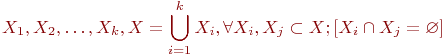 | (18.5) |
так, чтобы любые две смежные вершины 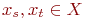 принадлежали разным подмножествам, т.е. чтобы рёбра графа
принадлежали разным подмножествам, т.е. чтобы рёбра графа 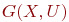 соединяли вершины из разных подмножеств
соединяли вершины из разных подмножеств
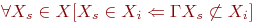 | (18.6) |
Отметим все вершины 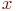 индексами
индексами 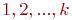 (т.е. раскрасим вершины
(т.е. раскрасим вершины 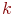 цветами), причём вершины внутри каждого подмножества
цветами), причём вершины внутри каждого подмножества 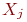 помечают одним индексом (раскрашивают одним цветом). Подмножества формируют таким образом, чтобы концы любого ребра графа имели различные индексы.
помечают одним индексом (раскрашивают одним цветом). Подмножества формируют таким образом, чтобы концы любого ребра графа имели различные индексы.
Наименьшее возможное число подмножеств, получаемое в результате такого разбиения вершин графа 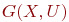 , называют хроматическим числом графа
, называют хроматическим числом графа 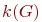 , граф
, граф 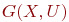 называют
называют 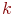 - хроматическим,а выражения (18.5) и (18.6)- хроматическим разложением
- хроматическим,а выражения (18.5) и (18.6)- хроматическим разложением  .
.
Особое значение имеет частный вид 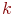 - хроматического графа - бихроматический или двудольный граф, для которого множество вершин
- хроматического графа - бихроматический или двудольный граф, для которого множество вершин  можно разбить на два непересекающихся подмножества
можно разбить на два непересекающихся подмножества 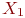 и
и 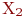 так, чтобы никакое ребро не соединяло бы вершины одного и того же подмножества, т.е.
так, чтобы никакое ребро не соединяло бы вершины одного и того же подмножества, т.е.
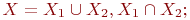 | (18.7) |
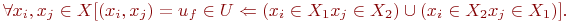
Такие графы называют графами Кёнига и обозначают 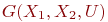 .
.
Критерий бихроматичности произвольного графа формулируется теоремой Кёнига, согласно которой обыкновенный граф 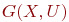 является бихроматическим тогда и только тогда, когда он не содержит циклов нечётной длины.
является бихроматическим тогда и только тогда, когда он не содержит циклов нечётной длины.
Если граф 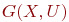 - дерево, т.е. в нём полностью отсутствуют циклы (существуют лишь циклы нулевой длины), то он является бихроматическим графом и может быть представлен в виде двудольного графа (рис. 18.1).
- дерево, т.е. в нём полностью отсутствуют циклы (существуют лишь циклы нулевой длины), то он является бихроматическим графом и может быть представлен в виде двудольного графа (рис. 18.1).
Граф Кёнига 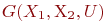 называют полным, если каждая вершина
называют полным, если каждая вершина 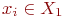 смежна с каждой вершиной
смежна с каждой вершиной 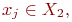 и наоборот.
и наоборот.
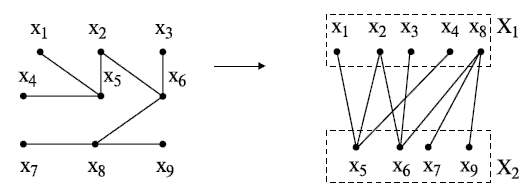
Рис. 18.1. Пример двудольного графа
Пример. Рассмотрим пример бихроматического графа 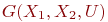 , у которого
, у которого
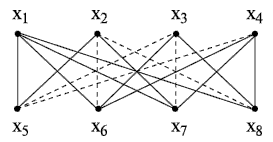
Рис. 18.2. Бихроматический граф
При добавлении к этому графу рёбер 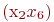 ,
, 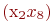 ,
, 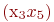 ,
, 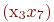 и
и 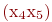 получим полный бихроматический граф. Очевидно, что подмножество
получим полный бихроматический граф. Очевидно, что подмножество 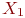 множества вершин
множества вершин  можно раскрасить в один цвет, а
можно раскрасить в один цвет, а 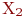 - в другой.
- в другой.
Число рёбер полного бихроматического графа 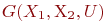
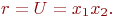
При составлении целого ряда алгоритмов проектирования РЭС используют операцию удаления некоторых вершин и рёбер графа. При этом особое значение приобретает понятие критического графа.
Граф 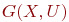 называют критическим, если удаление любой вершины
называют критическим, если удаление любой вершины 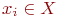 с инцидентными ей рёбрами уменьшает хроматическое число графа.
с инцидентными ей рёбрами уменьшает хроматическое число графа.
Критическим 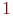 - хроматическим графом является одна вершина; критическим 2 - хроматическим - две вершины, соединённые ребром; критическим
- хроматическим графом является одна вершина; критическим 2 - хроматическим - две вершины, соединённые ребром; критическим 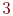 - хроматическим - простой цикл нечётной длины, так как при удалении из него любой вершины с инцидентными ей рёбрами получим двудольный граф. Очевидно, что полный граф всегда является критическим, причём его хроматическое число равно
- хроматическим - простой цикл нечётной длины, так как при удалении из него любой вершины с инцидентными ей рёбрами получим двудольный граф. Очевидно, что полный граф всегда является критическим, причём его хроматическое число равно
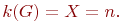
В отличие от цикломатического числа определение хроматического числа осуществляется с помощью сравнительно сложных алгоритмов, в основу большинства которых положены методы целочисленного линейного программирования.
Оценка хроматического числа через число вершин графа 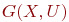 имеет вид:
имеет вид:
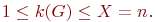
В этом выражении нижняя граница соответствует пустым, а верхняя - полным графам.
На практике для простых связных графов оценить величину  можно следующим образом.
можно следующим образом.
Сначала выбираем вершину с минимальной локальной степенью и пометим (раскрасим) её, затем произведём хроматическую раскраску вершин, смежных с данной, и так далее.
Например, для графа на рис. 18.2, б сначала выбираем вершину  для которой
для которой 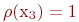 , и раскрасим её в красный цвет. Тогда вершину
, и раскрасим её в красный цвет. Тогда вершину 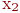 можно раскрасить в синий цвет, а вершины
можно раскрасить в синий цвет, а вершины 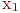 и
и 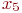 - в красный (они не смежны с
- в красный (они не смежны с 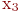 ). Вершины
). Вершины 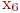 и
и 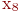 можно раскрасить в синий цвет, а оставшиеся вершины
можно раскрасить в синий цвет, а оставшиеся вершины 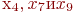 - в жёлтый. На раскраску вершин графа пошло три краски
- в жёлтый. На раскраску вершин графа пошло три краски 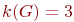 .
.
Знание хроматического числа графа позволяет в ряде случаев упростить алгоритмы, используемые на этапе конструкторского проектирования РЭС.
Пример. Рассмотрим задачу оценки числа слоёв многослойной печатной платы. Пусть, граф 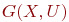 интерпретирует фрагмент коммутационного поля платы, где х - множество областей контактных площадок конструктивных элементов, внутри которых проведение проводников запрещено, a
интерпретирует фрагмент коммутационного поля платы, где х - множество областей контактных площадок конструктивных элементов, внутри которых проведение проводников запрещено, a 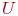 - множество трасс платы.
- множество трасс платы.
Построим граф пересечений 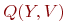 , в котором вершинами являются отдельные компоненты связности (электрические цепи) графа
, в котором вершинами являются отдельные компоненты связности (электрические цепи) графа 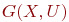 , причём
, причём 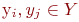 смежны, если соответствующие им компоненты связности
смежны, если соответствующие им компоненты связности 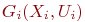 и
и 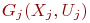 перекрывают друг друга.
перекрывают друг друга.
При этом хроматическое число 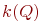 графа
графа 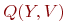 определит верхнюю границу числа коммутационных слоев рассматриваемого фрагмента платы (в нашем примере
определит верхнюю границу числа коммутационных слоев рассматриваемого фрагмента платы (в нашем примере 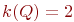 ). В этом случае цепи, соответствующие вершинам одного цвета графа
). В этом случае цепи, соответствующие вершинам одного цвета графа 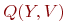 , можно располагать в одном слое печатной платы.
, можно располагать в одном слое печатной платы.
