Ограниченным средним временем пребывания в очереди
До сих пор мы рассматривали СМО с ожиданием, ограниченным только длиной очереди, то есть числом Е заявок, одновременно находящихся в очереди. В такой СМО, как известно, заявка, раз ставшая в очередь, уже не покидает ее и терпеливо дожидается обслуживания. На практике, однако, нередко встречаются и СМО другого типа, в которых заявка, подождав некоторое время, может уйти из очереди – так называемые «нетерпеливые» заявки. Мы будем рассматривать СМО подобного типа, оставаясь в рамках марковской схемы.
Предположим, что имеется m-канальная СМО с ожиданием, в которой число мест в очереди не ограничено. При этом, однако, среднее время пребывания заявки в очереди ограничено некоторым значением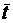 
. Тем самым на каждую заявку, стоявшую в очереди, действует своего рода дополнительный «поток уходов» с интенсивностью 
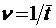. Ясно, что если этот поток носит пуассоновский характер, то процесс, протекающий в СМО, будет марковским. Найдем вероятности стационарных состояний для этого процесса.
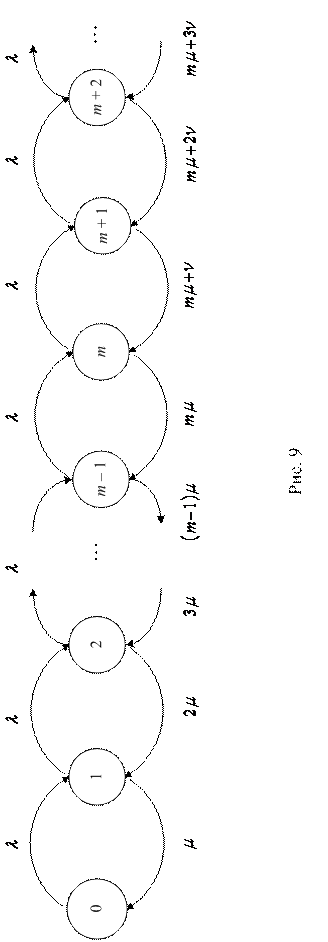
Граф состояний описанной системы имеет вид, изображенный на рис. 9. Как видим, что касается состояний с очередью, то в данном случае у стрелок, ведущих из этих состояний справа налево, стоят теперь суммарные интенсивности потоков обслуживаний всех m каналов (то есть mμ) плюс соответствующие интенсивности потоков уходов нетерпеливых заявок из очереди. Ясно, что если в очереди состоит, например, s заявок, то при этом суммарная интенсивность их уходов равна соответственно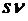 
.
Как видно из графа, перед нами опять классическая схема процесса гибели и размножения. Применив общие выражения для вероятностей предельных (стационарных) состояний в этой схеме, получим
; 
; 
;
; 
;
;
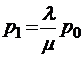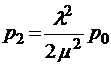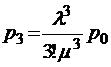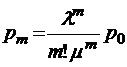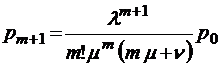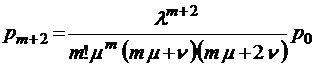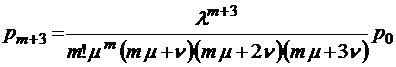
или в обозначениях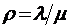 
и 
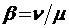(своего рода приведенная интенсивность ухода «нетерпеливых» заявок из очереди, параметр 
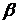показывает, сколько в среднем заявок покидает очередь необслуженными за среднее время обслуживания системой одной заявки)
; 
; 
;
; 
;
;
.
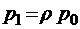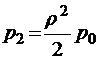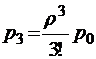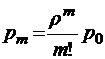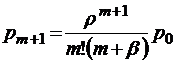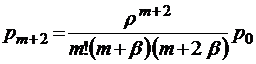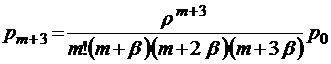В итоге имеем следующие формулы для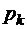 
:
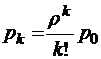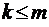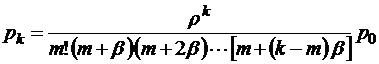при 
;
при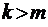 
. (2.5.1)
Запись формул (2.5.1) для 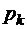можно упростить. В самом деле, разделим числитель и знаменатель второго из этих соотношений на 
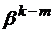. Тогда получим
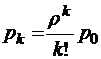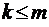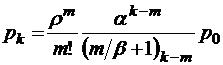при ; 
при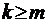 
,
где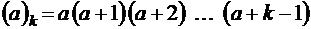 
; 
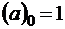– символ Похгаммера [14]. Величина 
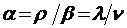, очевидно, показывает, какое среднее число заявок поступает в систему за среднее время пребывания «нетерпеливой» заявки в очереди. В этом случае из условия нормировки имеем
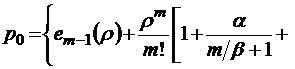
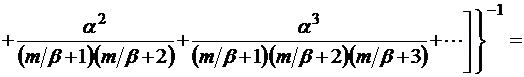
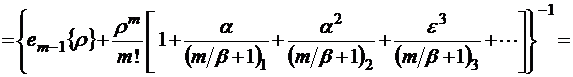
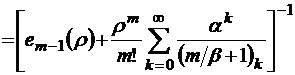. (2.5.2)
Рассмотрим более внимательно сумму в формуле (2.5.2). Ясно, что в отличие от соответствующих соотношений § 2.1 – 2.4, в которых суммы бесконечного или конечного числа слагаемых сводились к суммам бесконечной или конечной геометрических прогрессий, в формуле (2.5.2) содержится сумма бесконечного ряда, не являющегося такого рода прогрессией. Поэтому будем действовать следующим образом.
Заметив, что ex definition
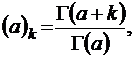
где Γ – гамма-функция, перепишем интересующую нас сумму как
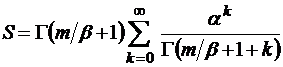, (2.5.3)
и тогда
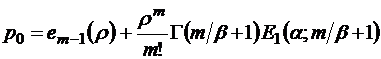, (2.5.4)
где
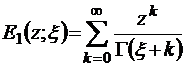(2.5.5)
– функция Миттаг–Леффлера первого порядка (обобщение показательной функции exp z). Эта функция хорошо известна специалистам в области теории функции комплексного переменного и интегральных преобразований [15, 16]. Выражение (2.5.4) в свою очередь можно еще больше упростить. Из формулы (2.5.5), очевидно, имеем
,
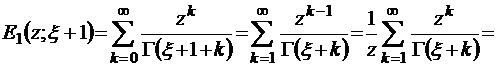
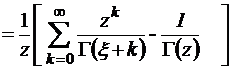так что
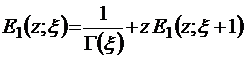(2.5.6)
– рекуррентная формула для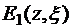 
, и тогда из соотношения (2.5.3) с учетом известного рекуррентного соотношения 
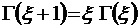следует
.
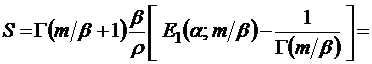
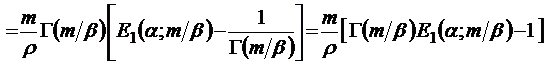В итоге соотношение (2.5.4) дает следующую формулу для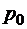 
:
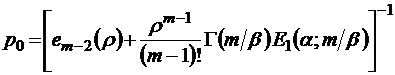(2.5.7)
(напомним, что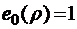 
и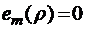 
для всех 
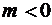). Для одноканальной CMО (m=1) формула (2.5.7) имеет особенно простой вид
.
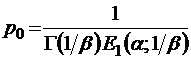В частности, при β=1 (то есть в том случае, когда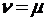 
) 
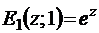, и тогда 
.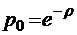