Модель М/М/1 или классическая СМО
Предположим, что мы имеем одноканальную СМО с однородным бесконечным простейшим потоком заявок и неограниченной очередью. Пусть интенсивность входящего потока заявок равна l, а длительность обслуживания одной заявки – случайная величина с математическим ожиданием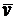 
.
Как было сказано выше, наряду с понятием средней длительности обслуживания мы будем использовать понятие интенсивности обслуживания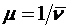 
– величину, обратную 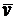и характеризующую число заявок, которое может обслужить прибор в единицу времени.
В этом случае, как уже говорилось, можно считать, что навстречу потоку заявок (требований), входящих в систему, движется поток обслуженных заявок (требований), исходящих из системы.
Поток обслуженных заявок также будем считать простейшим потоком (с интенсивностью m). В теории массового обслуживания принята символика Кендалла, впоследствии усовершенствованная рядом авторов [4]. В соответствии с этой символикой рассматриваемая система массового обслуживания условно обозначается как М/М/1. В этой символике первые два символа описывают распределение промежутков времени между двумя последовательными требованиями во входящем потоке и распределение времени их обслуживания, то есть являются символами соответственно входящего и исходящего потоков заявок. В данном случае буква М (от markovian – марковский) является символом простейшего потока, обладающего марковским свойством (свойством отсутствия последействия). Третий символ в аббревиатуре Кендалла обозначает число обслуживающих приборов. Очевидно, что в данном случае это единица.
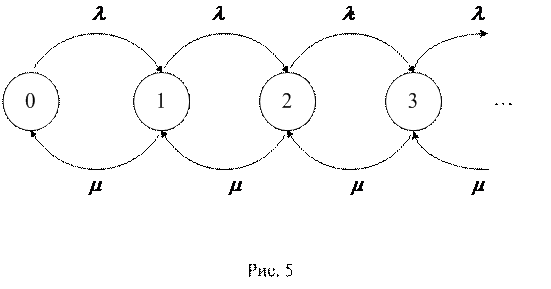
Выделив состояния СМО по числу заявок, находящихся в системе (0, 1, 2 и так далее), мы получим процесс с дискретными состояниями и непрерывным временем, граф состояний которого изображен на рис. 5 – уже знакомый нам процесс гибели и размножения. Применим общие формулы (1.5.4), (1.5.5) для расчета вероятностей стационарных состояний в этом конкретном случае.
Обозначим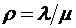 
(стандартное обозначение теории массового обслуживания, иногда эту величину называют приведенной интенсивностью входящего потока заявок, она показывает, сколько в среднем заявок поступает в систему за среднее время обслуживания этой системой одной заявки). Тогда, очевидно, формулы (1.5.4) дают
; 
; 
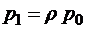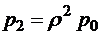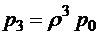
и так далее, так что общая формула для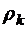 
имеет вид
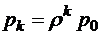, k = 1, 2,… ,
откуда с использованием условия нормировки (1.5.5) имеем
.
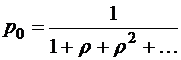Очевидно, что при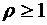 
ряд в знаменателе этого выражения расходится, и в этом случае число ожидающих обслуживания требований будет возрастать бесконечно. Стационарный режим (стационарное состояние) классической СМО устанавливается, таким образом, только в том случае, если 
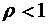. В противном же случае 
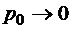, значит, и все
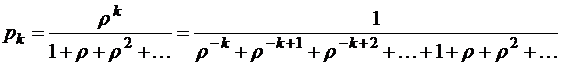
также стремятся к нулю. Если же 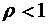, то ряд в знаменателе этих формул представляет собой обычную геометрическую прогрессию, сумма которой 
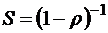согласно (П.3), так что
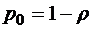, (2.1.1)
и тогда
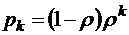. (2.1.2)
Последнее выражение представляет собой так называемое геометрическое распределение, хорошо известное в математической статистике.
Заметим также, что в приведенном выводе формул (2.1.1), (2.1.2) никак не участвовало начальное число i требований, находящихся в системе. Отсюда следует, что при сделанных предположениях установившийся режим классической СМО (когда он существует) не зависит от начальных условий.