Модели открытых систем массового обслуживания
ЧАСТЬ 2.
МОДЕЛИ ОТКРЫТЫХ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ
Сводка формул
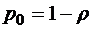 ;
; 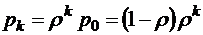 ;
; 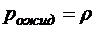 ;
;
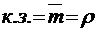 ;
; 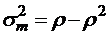 ;
;
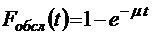 ;
; 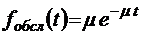 ;
; 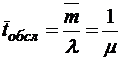 ;
; 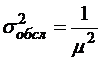 ;
;
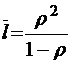 ;
; 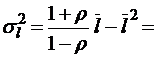
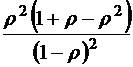 ;
;
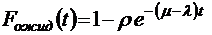 ;
; 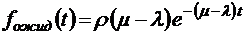 ;
;
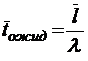
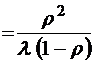 ;
; 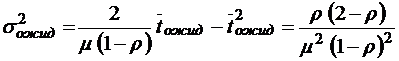 ;
;
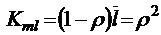 ;
; 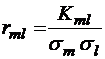
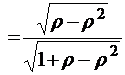 ;
;
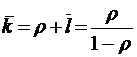 ;
; 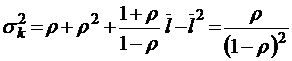 ;
;
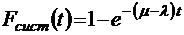 ;
; 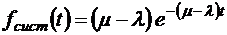 ;
;

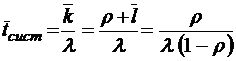 ;
;
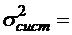
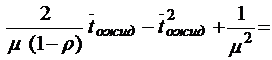
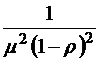 ;
;
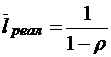 ;
; 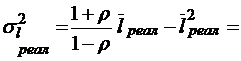
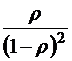 ;
;
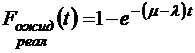 ;
; 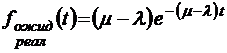 ;
;
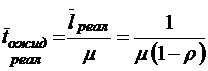 ;
; 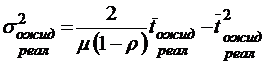
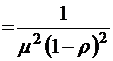 .
.
Модель М/М/m или многоканальное устройство
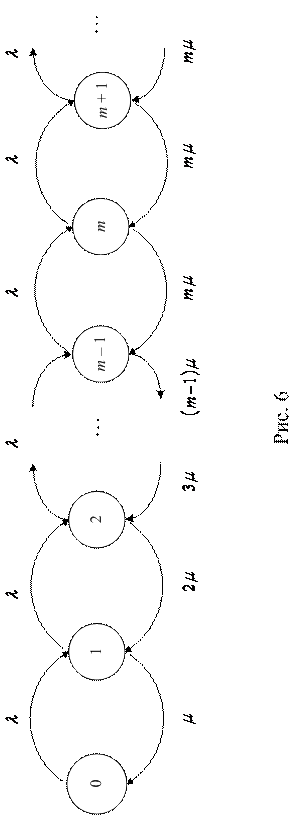
Предположим теперь, что изучаемая нами система массового обслуживания имеет m обслуживающих каналов с одинаковой интенсивностью обслуживания μ при общем простейшем входящем потоке заявок с интенсивностью λ. Такая система имеет условное обозначение М/М/m. Граф состояний этой системы подобен графу состояний одноканальной СМО (см. рис. 6).
Интенсивности перехода в соседнее правое состояние при этом определяются точно так же, как и у одноканальной СМО, интенсивностью входящего потока заявок λ – с приходом очередной заявки система приходит в следующее по порядку правое состояние. Иначе обстоит дело с интенсивностями у нижних стрелок. Пусть наша система находится в состоянии 1 – работает один канал, который обслуживает μ заявок в единицу времени, и тогда 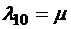 . Пусть теперь система находится в состоянии 2. Для перехода из этого состояния в состояние 1, очевидно, необходимо, чтобы закончили обслуживание и первый, и второй каналы (вместо этих заявок в систему поступает новая заявка из входящего потока). Это в свою очередь означает, что суммарная интенсивность обслуживания заявок этими двумя каналами составляет
. Пусть теперь система находится в состоянии 2. Для перехода из этого состояния в состояние 1, очевидно, необходимо, чтобы закончили обслуживание и первый, и второй каналы (вместо этих заявок в систему поступает новая заявка из входящего потока). Это в свою очередь означает, что суммарная интенсивность обслуживания заявок этими двумя каналами составляет 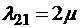 , и так далее: суммарный поток обслуживания
, и так далее: суммарный поток обслуживания 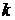 каналами имеет интенсивность
каналами имеет интенсивность 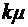 . При
. При 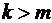 интенсивность обслуживания уже не меняется и сохраняется равной
интенсивность обслуживания уже не меняется и сохраняется равной 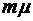 . Формулы (1.5.4) дадут в этом случае
. Формулы (1.5.4) дадут в этом случае
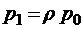 ;
; 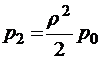 ;
; 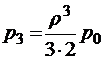 … ;
… ;
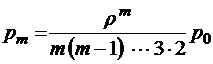 ;
; 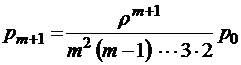 ;
;
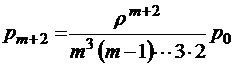
и так далее, так что в итоге получим
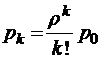 при
при 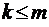 ;
; 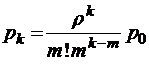 при
при 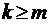 .
.
Условие нормировки 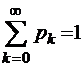 даст нам тогда
даст нам тогда
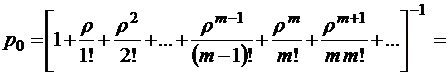
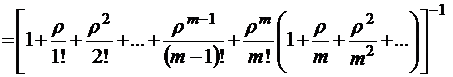 ,
,
откуда с учетом (П.3) имеем
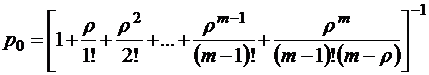
или
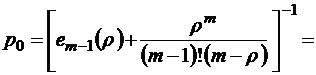
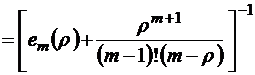 , (2.2.1)
, (2.2.1)
где 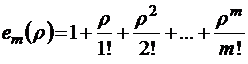 – неполная экспоненциальная функция (неполная экспонента). При этом
– неполная экспоненциальная функция (неполная экспонента). При этом 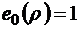 , а при
, а при 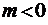 полагаем
полагаем 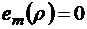 . Ясно, что
. Ясно, что 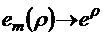 при
при 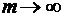 . Легко проверить, что при
. Легко проверить, что при 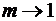 формула (2.2.1) переходит в соотношение (2.1.1) модели М/М/1. Очевидно также, что данная модель имеет стационарный режим для всех
формула (2.2.1) переходит в соотношение (2.1.1) модели М/М/1. Очевидно также, что данная модель имеет стационарный режим для всех 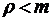 .
.
Итак, вероятности равновесных состояний системы найдены. Перейдем к вычислению числовых характеристик установившегося в системе стационарного режима.
Сводка формул
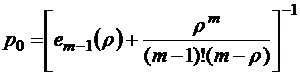 ;
;
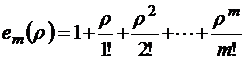 (неполная экспонента);
(неполная экспонента);
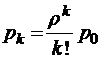 при
при 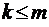 ;
; 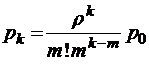 при
при 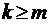 ;
;
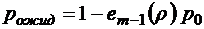
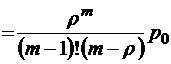 ;
;
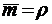 ;
; 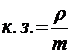 ;
; 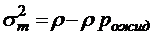 ;
;
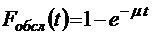 ;
; 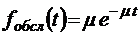 ;
; 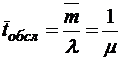 ;
; 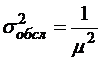 ;
;
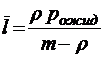 ;
; 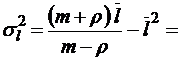
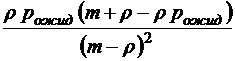 ;
;
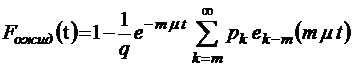
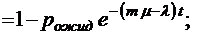
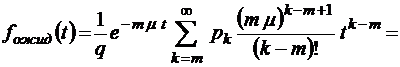
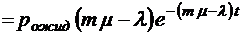 ;
; 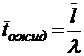
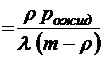 ;
;
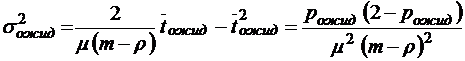 ;
;
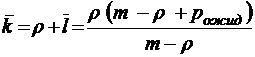 ;
; 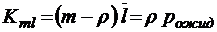 ;
;
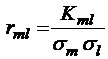
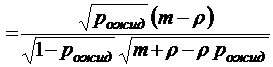 ;
;
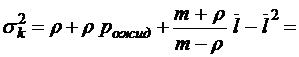

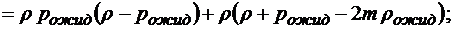
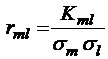
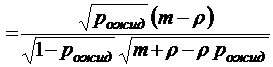 ;
;
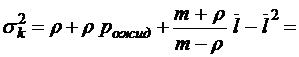
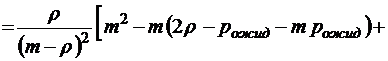
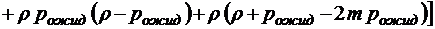 ;
;
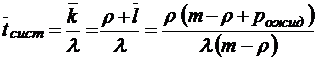 ;
;
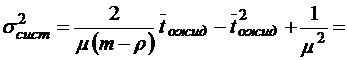
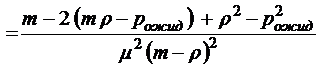 ;
;
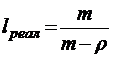 ;
; 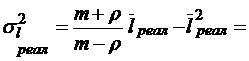
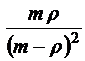 ;
;
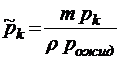 ;
; 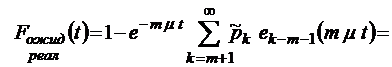
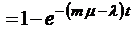 ;
;
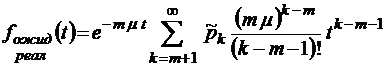
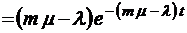 ;
;
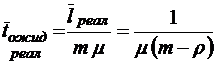 ;
;
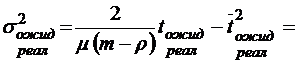
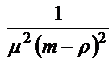 .
.
Сводка формул
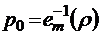 ;
; 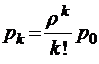 ;
;
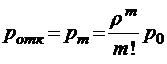 ;
; 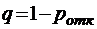 ;
; 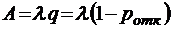 ;
;
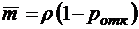 ;
; 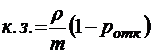 ;
; 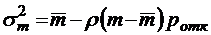 ;
;
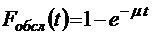 ;
; 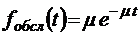 ;
; 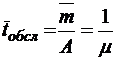 ;
; 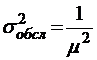 .
.
Модель М/М/m/Е или модель с очередью
Конечной длины
Рассмотрим теперь многоканальную систему массового обслуживания, для которой фиксировано максимальное число требований, ожидающих обслуживания; в частности, предположим, что в очереди одновременно могут находиться не более Е заявок и что любое поступившее сверх этого числа требование получает отказ и немедленно покидает систему без обслуживания. Поступление новых требований происходит по закону Пуассона, времена их обслуживания распределены экспоненциально со средней интенсивностью обслуживания μ заявок в единицу времени, но при этом в систему допускаются только те требования, которые застают в ней строго меньше заявок, чем m+E. Ясно, что при Е=0 такая система массового обслуживания сводится к СМО с отказами (модель М/М/m/0, изученная в предыдущем разделе).
Граф состояний такой системы изображен на рис. 8. Отсюда в соответствии с результатами, полученными в § 2.2 для аналогичной системы (там Е=∞), мы сразу можем записать результат решения уравнений Колмогорова для вероятностей стационарных состояний:
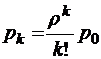 при
при 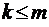 ;
;
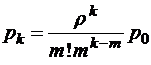 при
при 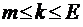 , (2.4.1)
, (2.4.1)
и тогда
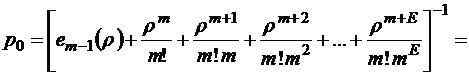
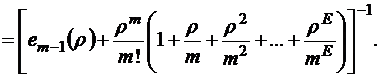
Отсюда в силу формулы (П.7) имеем
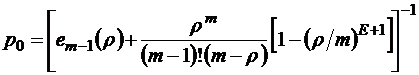 . (2.4.2)
. (2.4.2)
Заметим также, что последнюю формулу для 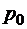 можно переписать в виде
можно переписать в виде
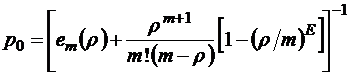 ,
,
что очевидно. При Е=0 формулы (2.4.1), (2.4.2) для 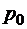 и
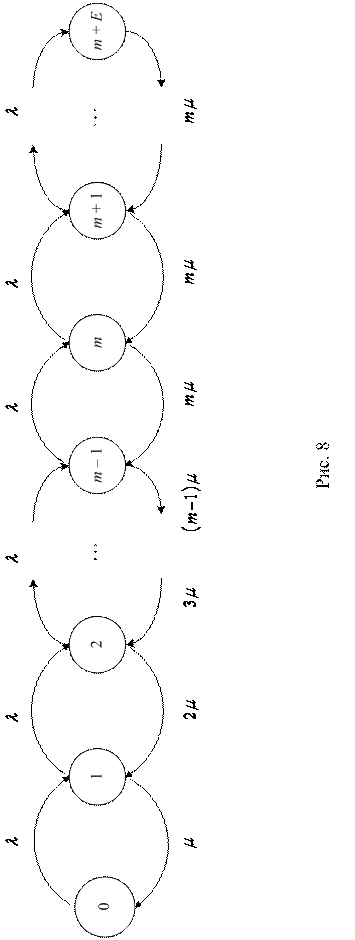
и 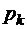 совпадают с полученными выше (§ 2.3), при Е→ ∞ и
совпадают с полученными выше (§ 2.3), при Е→ ∞ и 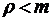 получаем аналогичные соотношения для модели M/M/m (§ 2.2), поскольку в этом
получаем аналогичные соотношения для модели M/M/m (§ 2.2), поскольку в этом
случае 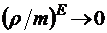 . Если же
. Если же 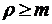 , то при Е→ ∞
, то при Е→ ∞
lim 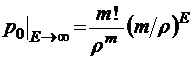 ,
,
то есть с ростом E стремится к нулю.
Данная модель работает при всех значениях параметра накачки (заявок в систему) ρ. Случай 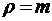 , однако, должен быть разобран особо, поскольку в этом случае знаменатель в формуле (2.4.2) содержит неопределенность типа
, однако, должен быть разобран особо, поскольку в этом случае знаменатель в формуле (2.4.2) содержит неопределенность типа 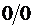 , раскрыв которую по правилу Лопиталя, имеем
, раскрыв которую по правилу Лопиталя, имеем
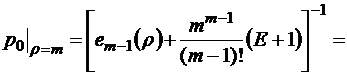
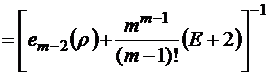 . (2.4.3)
. (2.4.3)
Заметим, что, как показывает практика, в действительности формула (2.4.3) начинает работать, то есть давать более точные значения 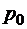 , чем формула (2.4.2), не только тогда, когда строго выполняются условия равенства
, чем формула (2.4.2), не только тогда, когда строго выполняются условия равенства 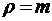 , но уже в некоторой окрестности значений параметра ρ вокруг точки
, но уже в некоторой окрестности значений параметра ρ вокруг точки 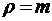 . Для достаточно больших E и
. Для достаточно больших E и 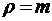 , очевидно,
, очевидно,
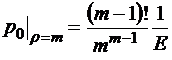 .
.
Сводка формул
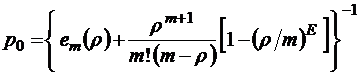 ;
;
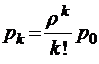 при
при 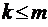 ;
; 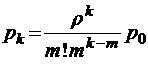 при
при 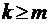 ;
;
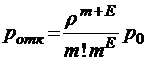 ;
;
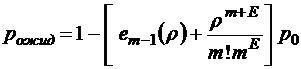
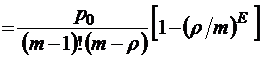 ;
;
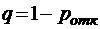 ;
; 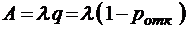 ;
;
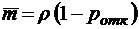 ;
; 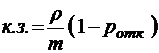 ;
;
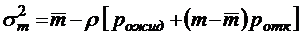 ;
;
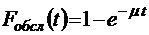 ;
; 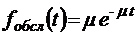 ;
; 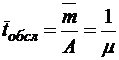 ;
; 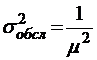 ;
;
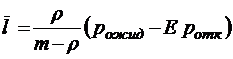 ;
; 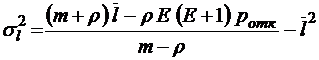 ;
;
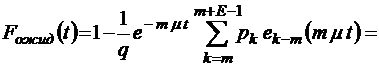
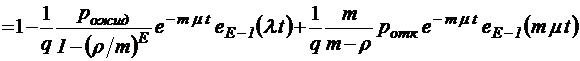 ;
;
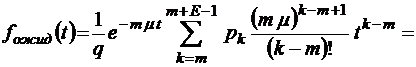
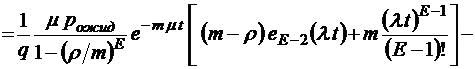
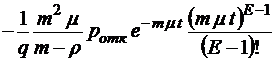 ;
;
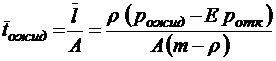 ;
;
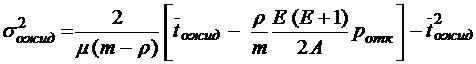 ;
;
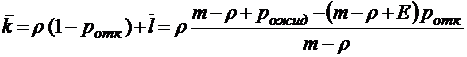 ;
;
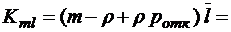
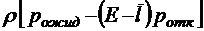 ;
;
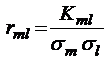 ;
; 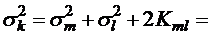
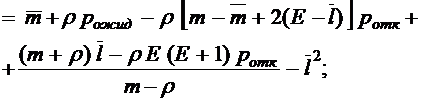
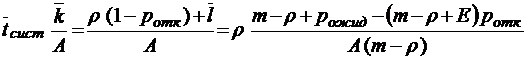 ;
;
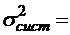
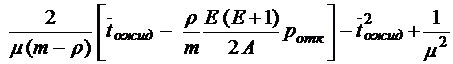 ;
;
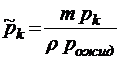 ;
; 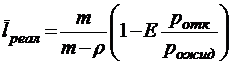 ;
;
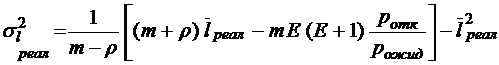 ;
;
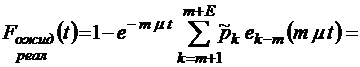
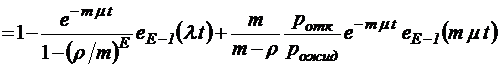 ;
;
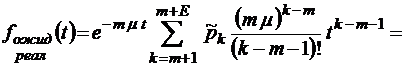
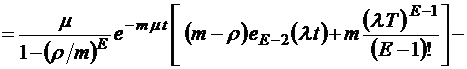
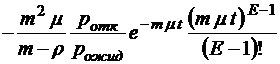 ;
;
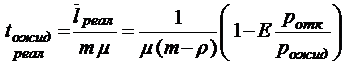 ;
;
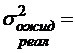
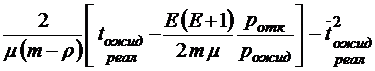 .
.
При ρ = m
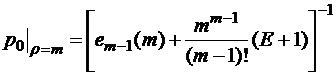 ;
;
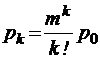 при
при 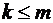 ;
; 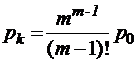 при
при 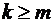 ;
;
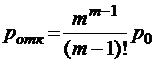 ;
; 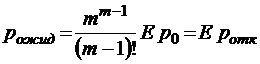 ;
;
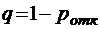 ;
; 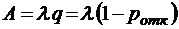 ;
;
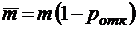 ;
; 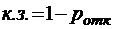 ;
; 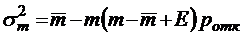 ;
;
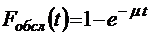 ;
; 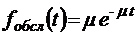 ;
; 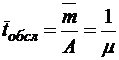 ;
; 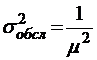 ;
;
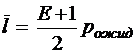 ;
; 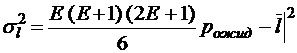 ;
;
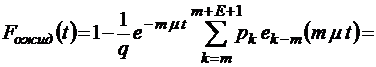
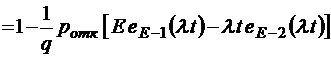 ;
;
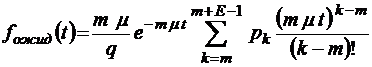
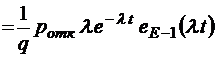 ;
;
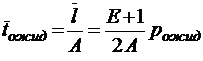 ;
; 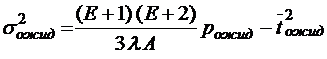 ;
;
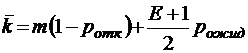 ;
;
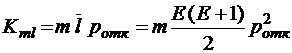 ;
; 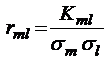 ;
;
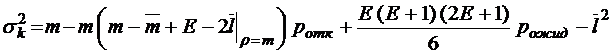 ;
;
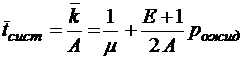 ;
;
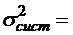
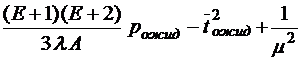 ;
;
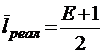 ;
; 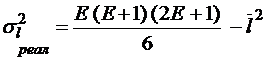 ;
;
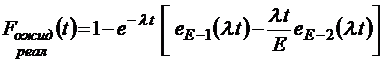 ;
;
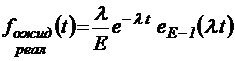 ;
; 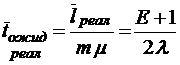 ;
;
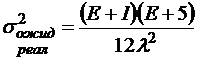 .
.
Сводка формул
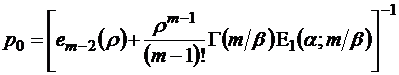 ;
;
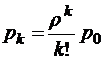 при
при 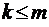 ;
; 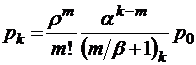 при
при 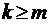 ;
;
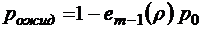
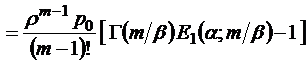 .
.
При малых 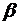
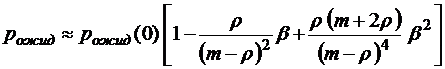 ;
;
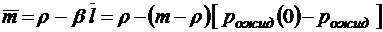 ;
;
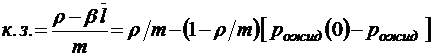 ;
;
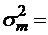
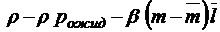 ;
;
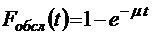 ;
; 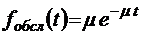 ;
; 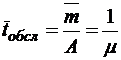 ;
; 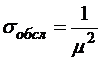 ;
;
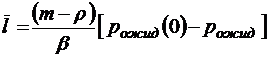 ;
; 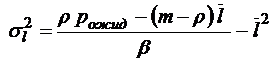 ;
;
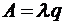 ;
; 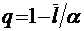 ;
;
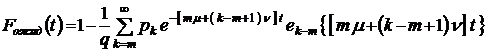 ;
;
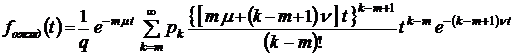 ;
;
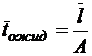
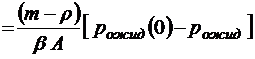 ;
;
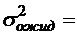
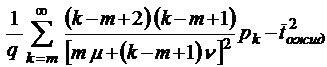 ;
;
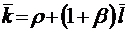 ;
; 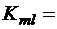
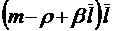 ;
; 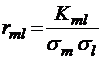 ;
;
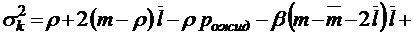
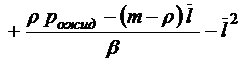 ;
;
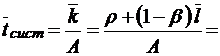
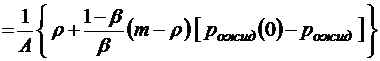 ;
;
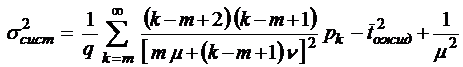 ;
;
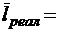
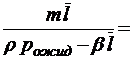
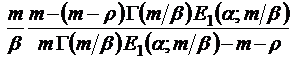 ;
;
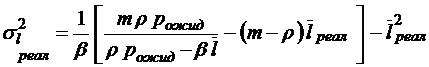 ;
;
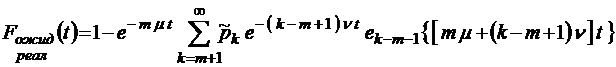 ;
;
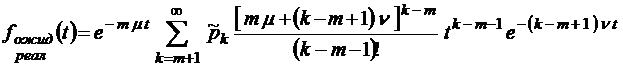 ;
;
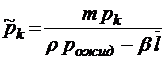 ;
; 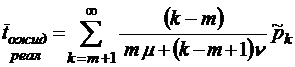 ;
;
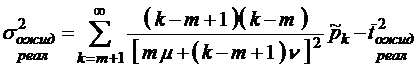 .
.
Заметим, что формализацию этой модели можно осуществить и с использованием вырожденной гипергеометрической функции Куммера
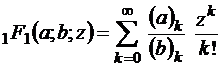 ,
,
то есть 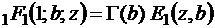 , поскольку
, поскольку 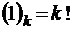 . В этом случае, очевидно,
. В этом случае, очевидно,
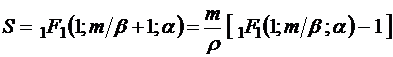 ,
,
так что
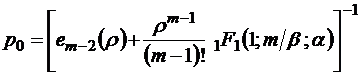 ;
;
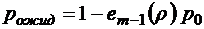
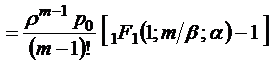 .
.
Все же остальные формулы остаются без изменений.
Легко также видеть, что полученные выше формулы останутся справедливыми и для модели открытой системы массового обслуживания с ограниченным средним временем пребывания в системе при очевидной замене 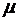 на
на 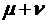 , то есть
, то есть 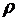 на
на 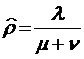 и
и 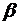 на
на 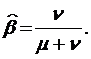 Первая из этих величин, очевидно, означает среднее число поступивших в систему заявок за среднее время, в течение которого заявка находится в обслуживающем приборе, а вторая – среднее число заявок, покинувших систему за то же самое время необслуженными.
Первая из этих величин, очевидно, означает среднее число поступивших в систему заявок за среднее время, в течение которого заявка находится в обслуживающем приборе, а вторая – среднее число заявок, покинувших систему за то же самое время необслуженными.
ЧАСТЬ 2.
МОДЕЛИ ОТКРЫТЫХ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ
