Ценные бумаги с фиксированным доходом

К ценным бумагам с фиксированным доходом относятся:

- облигации;

- привилегированные акции;

- векселя.

Рассмотрим безрисковые ценные бумаги на примере облигаций.

Облигацией называется ценная бумага, удостоверяющая отношения займа между их владельцем и лицом, выпустившим документ (эмитентом). Основные параметры облигации: номинальная цена или номинал, выкупная цена или правило её определения, если она отличается от номинала, дата погашения, норма доходности или купонная процентная ставка, дата выплат купонных процентов и курсовая цена. Номинальная цена напечатана на облигации и используется для начисления процентов. В современной практике выкуп по номиналу является преобладающим. Курсовая цена облигации определяется конъюнктурой рынка.

Для облигаций можно предложить классификацию по следующим признакам.

1. По методу обеспечения:

- государственные и муниципальные облигации, выплаты по которым обеспечиваются гарантиями государства или муниципалитета;

- облигации частных корпораций – обеспечиваются залогом имущества, доходами от различных программ и проектов;

- облигации частых корпораций без специального обеспечения.

2. По сроку:

- облигации с фиксированной датой погашения;

- без указанной даты погашения или бессрочные.

3. По способу погашения номинала:

- разовым платежом;

- распределёнными во времени погашениями оговоренных долей номинала.

- последовательными погашениями доли общего количества облигаций, соответствующие облигации называются серийными; часто этот метод погашения осуществляется с помощью лотерей.

4. По методу выплаты дохода:

- выплачиваются только купонные проценты, срок выкупа не оговаривается (бессрочные облигации);

- выплата купонных процентов не предусматривается, так называемые облигации с нулевым купоном;

- проценты выплачиваются вместе с номиналом;

- периодически выплачиваются проценты, а в конце срока – номинал, или выкупная цена, этот вид облигаций является преобладающим.

Купоны – это талоны с напечатанной на них процентной ставкой. Для получения процентного платежа купон вырезается и предъявляется эмитенту. Выплаты купонных процентов производятся ежегодно, по полугодиям или поквартально, а иногда в конце срока. Процентная купонная ставка обычно постоянная, правда, иногда выпускают облигации с «плавающей» процентной ставкой, уровень которой устанавливается в зависимости от каких-либо внешних условий. В случае, когда выкупная цена облигации отличается от номинала, купонные проценты начисляются на сумму номинала, а прирост капитала инвестора образуется за счет разности между выкупной ценой облигации и её ценой покупки.

Рассмотрим облигацию с номиналом 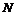, купонной процентной ставкой с, сроком до погашения n. Будем считать, что среднерыночный безрисковый процент равен i. Текущей стоимостью облигаций называется современное значение потока платежей, генерируемого данной облигацией

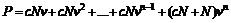, (1.2.1)

где 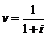- дисконтирующий множитель.

Текущая стоимость в случае нулевых купонов, когда обладатель облигации процентный платеж не получает, определяется так:

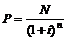. (1.2.2)

В случае, когда проценты начисляются за весь срок и выплачиваются одной суммой вместе с номиналом, текущая стоимость определяется формулой

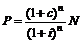. (1.2.3)

Полной доходностью будем называть решение предыдущих уравнений относительно процентной ставки i , если вместо текущей стоимости в уравнение поставить рыночную стоимость.

Пример 1.2.1. Найти полную доходность облигации номиналом 1000 р., если её рыночная стоимость равна 1180 р., купонная ставка 20%, со сроком до погашения 2 года.

Решение. По условию известно, что 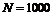, , 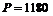, 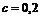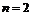. Тогда, используя формулу (1.2.1) получаем выражение

,

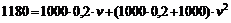которое является квадратным уравнением относительно v

,

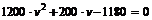дискриминант

,

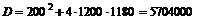отсюда

.

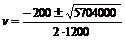Первое значение не удовлетворяет условию задачи

,

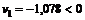второе

.

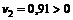Так как 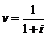, имеем 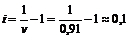- полная доходность облигации.

Купоны по облигациям могут выплачиваться чаще, чем один раз в год. В этом случае формула (1.2.1) примет вид

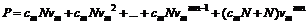, (1.2.4)

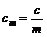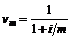где , а , i – годовая номинальная процентная ставка, m – частота купонных выплат в году.

Упражнения

1. Рыночная стоимость облигации в настоящее время $36. Год назад она стоила $33. Недавно были выплачен купонный платеж в размере $3. Определить полную доходность облигации.

2. Определить текущую стоимость облигации с номиналом 1200 р., купонной процентной ставкой 12% годовых и среднерыночным безрисковым процентом, равным 8%, если срок до погашения 2 года.

3. Определить номинал облигации с годовыми купонами 15%, рыночной ценой 1500 р., сроком до погашения 4 года и полной доходностью 12%.

4. Иванов купил в январе 2002 облигацию с номиналом в 1100 р. и сроком до погашения 2 года за 1195 р. В январе 2003 года он продал её Петрову за 1150 р. Определить купонную ставку и полную доходность облигации.

5. Определить цену облигации с номиналом 1000 р., сроком до погашения 3 года, годовой купонной процентной ставкой 20%, если купон выплачивается 2 раза в год. Среднерыночный процент равен 0,15.

6. Определить доходность облигации с нулевым купоном, если рыночная стоимость 850 р., номинал 1000 р., срок до погашения 2 года.

7. Петров владеет облигацией, номинальная стоимость которой равна 5000 р., а срок до погашения 3 года. Ежегодные купонные платежи составляют по ней 375 р., первый будет сделан через год. Текущий курс этой облигации составляет 4877,4 р. Среднерыночный процент 0,1. Стоит ли ему держать эту облигацию или её лучше продать?

8. Мелкая фирма обратилась к местному банку с просьбой предоставить фирме двухгодичную ссуду размером 30000 р. под 18% годовых и единовременным возвратом всей ссудной суммы с процентами в конце срока. На эти деньги фирма купила 10 безрисковых ценных бумаг с номиналом 3500 р., сроком до погашения 2 года, купонной ставкой 15%. Первая купонная выплата будет сделана через год. Определить прирост капитала после уплаты ссудной суммы с процентами, если среднерыночный процент 12% годовых? Какой должна быть минимальная купонная ставка, чтобы прирост капитала был положительный?

Рисковые ценные бумаги

Одними из наиболее распространенных рисковых ценных бумаг являются обыкновенные акции.

Существует много подходов к анализу рынка акций, но большая часть этих подходов относится к двум основным направлениям:

- техническому анализу;

- фундаментальному анализу.

Технический анализ в его простейшей форме изучает конъюнктуру курсов рынков акций с тем, чтобы дать прогноз динамики курсов акций конкретной формы. Первоначально прогнозируется исследование курсов за прошедший период с целью выявления повторных тенденций или циклов. Затем анализируются курсы акций за последний период времени с тем, чтобы выявить текущие тенденции, аналогичные обнаруженным ранее. Это сопоставление существующих тенденций с прошлыми осуществляется исходя из предположения, что ценовые тренды периодически повторяются.

Фундаментальный анализ исходит из того, что «истинная» (текущая, внутренняя) стоимость любого функционального актива равна приведенной стоимости всех денежных потоков, которые владелец актива рассчитывает получить в будущем. В соответствии с этим определяет время поступления и величину этих денежных потоков, а затем рассчитывает приведенную стоимость, используя соответствующую ставку дисконтирования. Таким образом, аналитик должен оценить ставку дисконтирования, спрогнозировать величину дивидендов, которые будут выплачены в будущем по акциям. Последнее эквивалентно вычислению показателей прибыли фирмы в расчете на одну акцию и коэффициент выплаты дивидендов. После того, как внутренняя стоимость акции определена, она сравнивается с текущим рыночным курсом акции. Акции, внутренняя стоимость которых меньше рыночного курса, называются переоцененными. А те акции, рыночный курс которых меньше внутренней стоимости, называются недооцененными. Аналитики-фундаменталисты считают, что любые случаи существенно неверной оценки исправляются впоследствии рынком.

Акции имеют номинальную, эмиссионную, ликвидационную, рыночную цену.

Одной из основных характеристик акции является номинальная стоимость. Номинальная цена указана на бланке, которая отражает долю установленного капитала, приходящегося на одну акцию в момент учреждения общества. Она для всех обыкновенных акций одного вида должна быть одинаковой. Номинальная стоимость, как правило, не совпадает с рыночной. У хорошо работающего акционерного общества она обычно выше рыночной, а у предприятия, испытывающего финансовые и производственные трудности - ниже.

Эмиссионная цена – это цена, рассчитанная по балансу, как отношение стоимости чистой акции к общему числу выпущенных акций.

Ликвидная цена справедлива в момент ликвидации общества.

Рыночная цена – это цена, по которой акция котируется на вторичном рынке. Она определяется в результате взаимодействия спроса на акции и предложения. На вторичном рынке цена акции может принимать любые значения.

Доход по акциям может быть представлен в двух формах – в виде прироста курсовой стоимости и в качестве периодических выплат –
дивидендов. Таким образом, текущую стоимость акции с выплатой дивидендов можно определить по формуле

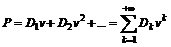, (1.3.1)

где 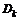- дивиденды, выплаченные в k-ый год.

Рыночная цена акций является предметом построения математических моделей. Существует значительное число работ, посвященных анализу колебаний стоимости акций на рынке, сама природа рыночной экономики делает невозможным безошибочное прогнозирование рыночных курсов.

С точки зрения математики, рыночная стоимость акции S(t) обычно моделируется тем или иным случайным процессом. Первая попытка описать этот процесс приписывается Л. Башелье, который в 1900 году в своей диссертации предложил модель случайного процесса, позднее строго описанного Н. Виннером для совершенно других задач. Дальнейшее исследование фондового рынка привели к уточнению этой модели. В модели Башелье стоимости могли быть отрицательными, и в 60-х годах американский математик П. Самуэльсон предложил модель только с неотрицательными стоимостями.

Как уже говорилось, ценная бумага характеризуется будущей стоимостью или доходностью. Помимо этого, рисковые ценные бумаги характеризуются уровнем риска – возможностью неполучения предполагаемых будущих доходов. Это неотъемлемая черта экономической реальности – с каждым деловым решением, как правило, связан определенный риск. В случае финансовых операций мерой такого риска является непредсказуемая изменчивость доходности того или иного инструмента. Формальным аппаратом описания таких ситуаций является теория вероятностей, основным объектом которой является вероятностное пространство 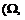F, Р), где Ω= 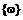- множество элементарных исходов, F – набор подмножеств Ω, образующих 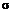-алгебру событий, о вероятности которых имеет смысл говорить в данной модели, Р – вероятностная мера событий, т.е. неотрицательная функция множеств 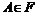, такая, что величина 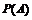имеет смысл вероятности осуществления события А, или, другими словами, наступления элементарного события .

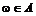Применительно к задачам финансовой математики модель теории вероятностей предполагает, что, в частности, будущая стоимость ценной бумаги 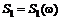является случайной величиной, т.е. функцией элементарных исходов 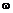. Тогда по формуле (1.1.2) доходность

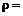
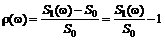(1.3.2)

тоже является случайной величиной, как функция от случайной величины. Поэтому в дальнейшем будем работать с доходностью ценной бумаги.

Её изменчивость может быть охарактеризована величиной дисперсии доходности

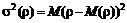, (1.3.3)

где 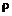- случайная доходность, M – символ математического ожидания, 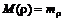– математическое ожидание или среднее значение доходности.

Интуитивно риск инвестиции представляет собой нечто вроде вероятности нежелательного события, когда цена или доходность некоторой ценной бумаги сильно отклоняются от прогнозируемого значения.

Покажем, что эта вероятность может быть оценена через среднее квадратическое отклонение 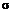. Действительно,

.

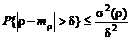Это неравенство известно, как неравенство Чебышева. Оно позволяет оценить сверху вероятность неблагоприятных событий. Видно, что оценка вероятности больших отклонений от среднего значения пропорциональна дисперсии. В силу этого в финансовой математике в качестве меры риска часто принимают дисперсию 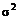или среднеквадратическое отклонение .

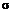Пример 1.3.1. Доходность акции есть случайная величина, принимающая с равными вероятностями значения 0,1 и 0,12. Составить прогноз ожидаемой доходности акции в будущем .

Решение. Запишем закон распределения вероятностей доходности в виде

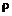	0,1	0,12
P	0,5	0,5

Тогда математическое ожидание будет

,

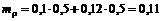дисперсия

,

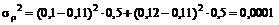а среднее квадратическое отклонение

.

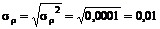Таким образом, наиболее вероятные значения доходности будут лежать в интервале .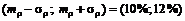

Пример 1.3.2. Будущая стоимость акции есть случайная величина, равномерно распределённая на интервале (1800, 2400). Определить математическое ожидание и среднее квадратическое отклонение стоимости.

Решение. Плотность вероятностей для случайной величины будущей стоимости 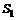имеет вид

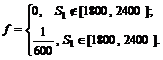
Тогда ожидаемая стоимость, то есть математическое ожидание случайной величины 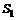, будет равно

,

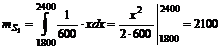а дисперсия и среднее квадратическое отклонение соответственно

,

.

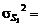
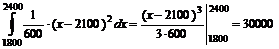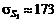Значит, ожидаемая стоимость акции будет равна 2100, а среднее квадратическое отклонение 173.

Упражнения

1. В начале года Петров вложил в акцию известной фирмы 2000 р. В конце года его акция стала стоить 2500 р. Также в конце года по акции были выплачены дивиденды в размере 100 р. Какова доходность акции?

2. Будущая стоимость акции есть случайная величина, равномерно распределённая на интервале (800, 1500). Найти прогнозируемое значение доходности и дисперсию этой доходности, если известно, что сейчас эта акция стоит 1000 р.

3. В условиях предыдущей задачи определить вероятность того, что будущая стоимость акции не превысит стоимости в настоящее время.

4. Решить задачу 3 при условии, что будущая стоимость акции есть дискретная случайная величина с законом распределения:

Х
Р	0,3	0,2	0,5

5. Имеются акции с доходностями, равномерно распределёнными на интервалах ( 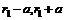), ( ), 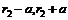, 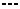где 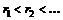, а – некоторое положительное число. Разумно ли, что акции с более высокими доходностями в большей степени подвержены риску? Почему?

6. Определить вероятность того, что абсолютная доходность акции будет лежать в интервале (120, 150), если известно, что она является нормально распределенной случайной величиной. Прогнозируемое значение её равно 140, а изменчивость доходности (её дисперсия) 36.

7. Специалист в области финансов определил потенциальные курсы акций стоимостью 1000 р. за штуку в конце года и сопутствующие вероятности для двух последующих лет. В первый год акции имеют 40% шансов подняться до 2000 р. и 60 % шансов упасть до 800 р. Если за первый год акции поднимутся до 2000 р., у них есть 50% шансов подняться до 2500 р., и 50% шансов упасть до 1500 р. во второй год. А если акции упадут до 800 р. за первый год, то 85% шансов у них будет упасть до 600 р. и только 15% подняться до своей первоначальной цены. Вычислить ожидаемую стоимость акций в конце второго года.