Элементы корреляционного анализа

Понятие функциональной,

Статистической и корреляционной зависимости.

Две случайные величины 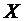и могут быть связаны функциональной зависимостью, либо зависимостью другого рода, либо быть независимыми.

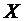Зависимость величины от называется функциональной, если каждому значению величины 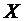соответствует единственное значение .

Строгая функциональная зависимость в окружающем нас мире встречается редко, так как обе величины 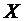и , или одна из них , подвержены еще действию случайных факторов. Если среди этих факторов есть общие для обеих величин, то в этом случае возникает статистическая зависимость.

Статистической называется зависимость, при которой изменение одной величины влечет изменение распределения другой.

Если изменение одной из переменных сопровождается изменениями условного среднего значения другой переменной величины, то такая зависимость является корреляционной.

Условным средним называют среднее арифметическое значений , соответствующих значению .

Например, пусть при случайная величина приняла значения , , . Тогда условное среднее равно .

Если каждому значению 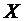соответствует одно значение условной средней, то условная средняя есть функция от . В этом случае говорят, что случайная величина зависит от 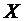корреляционно.

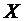Корреляционной зависимостью от называют функцию .

Уравнение называют уравнением регрессии на 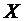, а ее график – линией регрессии на .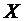

Аналогично определяется условная средняя и корреляционная зависимость 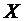от .

Условным средним называется среднее арифметическое значений 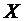, соответствующих .

Корреляционной зависимостью 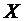от называют функцию .

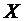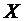Уравнение называют уравнением регрессии на , а ее график – линией регрессии на .

Корреляционный анализ рассматривает две задачи.

Первая задача теории корреляции – установить форму корреляционной связи, то есть вид функции регрессии (линейная, квадратичная и так далее).

Вторая задача теории корреляции – оценить силу (тесноту) корреляционной связи. Теснота корреляционной связи (зависимости) на 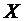оценивается по величине рассеивания значений вокруг условного среднего. Большое рассеивание свидетельствует о слабой зависимости от 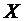, малое рассеивание указывает на наличие сильной зависимости.

Отыскание параметров выборочного уравнения линейной регрессии

По несгруппированным данным

Пусть имеются две случайные величины, и проводится их измерение.

В результате независимых опытов получены, пар чисел , , ,

Будем искать линейное выборочное уравнение регрессии на в виде:

Так как по выборочным данным можно получить только оценки параметров, то оценку коэффициента обозначим через , а оценку — через , то есть .

Параметры и находим методом наименьших квадратов по формулам:

,

Аналогично находится выборочное уравнение линейной регрессии на :

,

где

,

.

Для оценки связи (тесноты) между случайными величина­ми обычно используется выборочная ковариация и выборочный коэффициент корреляции.

Выборочная ковариация (эмпирический корреляционный момент) записывается в виде:

,

а выборочный коэффициент корреляции имеет вид:

или ,

где , .

Абсолютная величина (модуль) выборочного коэффициента корреляции не превосходит единицы, то есть или . С возрастанием линейная корреляционная зависимость становится более тесной, и при переходит в функциональную. Если , то корреляционная связь испытаний и отсутствует.

Пример 11. В результате независимых испытаний получены пары значений случайных величин и :

В таблице значения расставлены в возрастающем порядке.

Найти выборочное уравнение линейной регрессии и выборочный коэффициент корреляции. Построить прямые регрессии на и на .

¦ Составим таблицу подсчетов ( табл.16 ).

Таблица 16

Номер опыта

1) Находим , .

2) , .

, .

3) Вычислим эмпирический корреляционный момент:

.

Тогда коэффициент корреляции: .

Значение довольно близко к 1, следовательно, связь между случайными величинами и довольно тесная.

4) Найдем уравнения линий регрессии

на :

на :

5) Построим линии регрессии ( Рис.6) . Для этого найдем точки пересечения линий с осями координат:

: , ;

,

: , ;

, .

Рис.6 ?