Разделенные разности. Интерполяционный многочлен в форме Ньютона

Для функции 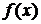и узлов интерполяции

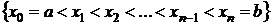
разделенными разностями первого порядка называют отношения

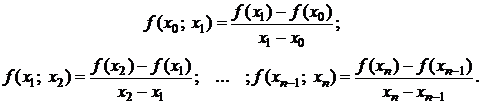(4.4)

На основе разделенных разностей первого порядка вычисляют разделенные разности второго порядка

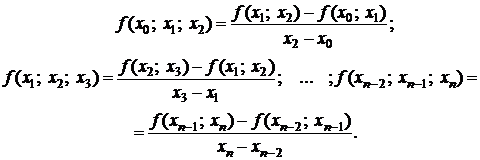(4.5)

Вообще, если определены конечные разности 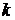- го порядка 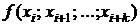, то разделенные разности ( 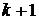) - го порядка находят при помощи формулы

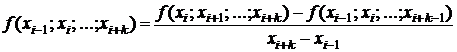. (4.6)

Таким образом, для ( 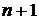) узлов интерполяции могу быть построены разделенные разности до 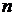- го порядка включительно; разделенные разности более высоких порядков равны нулю.

Для вычисления разделенных разностей удобно пользоваться табличной формой. Такая таблица разделенных разностей имеет следующий вид (для примера взят случай ):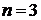

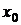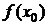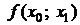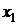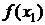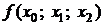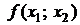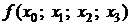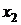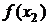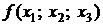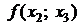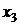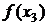Интерполяционный многочлен Лагранжа выражается через разделенные разности следующей формулой:

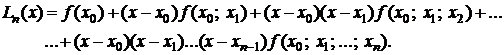(4.7)

Эта форма записи интерполяционного многочлена и носит название интерполяционного многочлена Ньютона.

П р и м е р 3. Применим формулу (4.7) к данным, приведенным в примерах 1 и 2.

•

		Разделенные разности
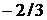		–1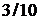

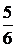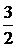В таблице выделены значения функции и разделенных разностей, которые войдут в формулу (4.7):

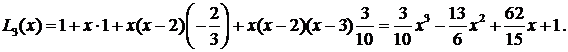
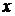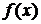		Разделенные разности
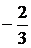		–1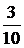

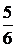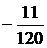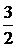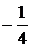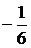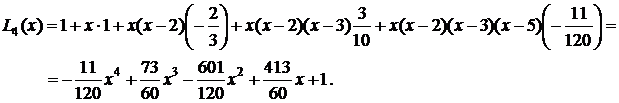
Численное интегрирование

Задача численного интегрирования. Если для функции 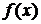, определенной на отрезке 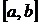, можно найти первообразную 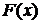, то определенный интеграл 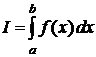можно вычислить по формуле

=

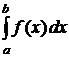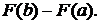
Но на практике, как правило, найти первообразную 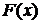через элементарные функции не удается либо она слишком сложна для вычислений. В этих случаях прибегают к формулам численного интегрирования.

Хотя из определения интеграла 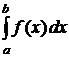и следует, что с помощью интегральной суммы 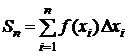его можно найти с любой точностью, но этот прием замены определенного интеграла интегральной суммой практически мало пригоден из-за медленной сходимости 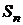к 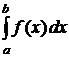с увеличением .

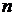Для получения формул численного интегрирования используют замену функции 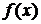некоторой приближающей функцией 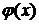. Чаще всего подынтегральную функцию заменяют интерполирующим многочленом Лагранжа различной степени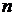

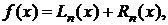(6.1)

где 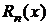– остаточный член интерполяции. Тогда

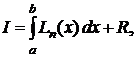(6.2)

где 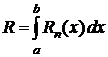– остаточный член формулы численного интегрирования (погрешность этой формулы).

При численном интегрировании обычно рассматривают разбиения отрезка интегрирования 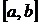на равные части (если, конечно, это разбиение не задается таблицей функции 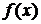). При произвольном разбиении оценка погрешности, как правило, значительно осложняется.

Пусть отрезок 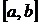разделен на 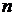равных частей точками

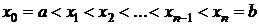(равномерная сетка),

т. е. 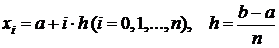– шаг сетки. Обозначим через 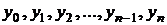соответствующие значения функции .

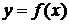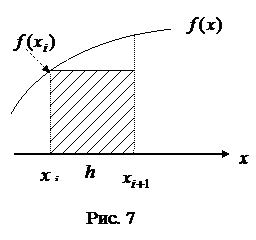Формулы прямоугольников. Подынтегральная функция 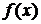заменяется на каждом 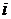-ом шаге сетки интерполяционным многочленом Лагранжа нулевой степени 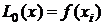, , 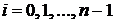( 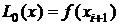при перемещении по сетке справа налево). В случае 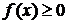это означает, что площадь каждой полоски, на которые разбивается криволинейная трапеция, заменяется площадью прямоугольника высотой 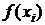и основанием 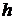(рис. 7).

Подынтегральную функцию можно также заменить ее значением в середине каждого отдельного интервала сетки 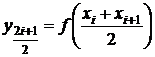( 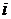=0, 1, …, 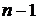), но в том случае, если она задана таблицей, это значение приходится находить, как правило, интерполированием, что вносит дополнительную погрешность (трудно поддающуюся оценке).

В зависимости от выбора значения интерполяционного многочлена Лагранжа нулевой степени на каждом шаге сетки получаются следующие формулы прямоугольников:

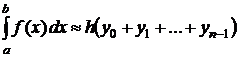, (6.3)

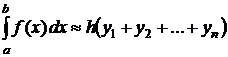, (6.4)

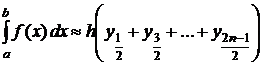. (6.5)

Для аналитически заданных подынтегральных функций 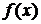в большинстве случаев при данном 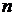формула (6.5) точнее, чем (6.3) и (6.4). Предельная погрешность этой формулы составляет:

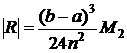, (6.6)

где 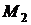– наибольшее значение 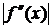на отрезке 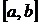. Эта погрешность асимптотически стремится к нулю при .

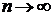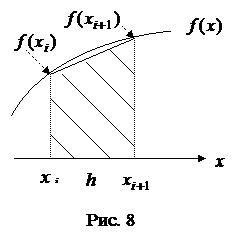Формула трапеций. Подынтегральная функция 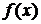заменяется на каждом 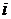-ом шаге сетки интерполяционным многочленом Лагранжа первой степени 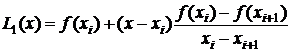, 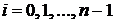. В случае 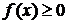это означает, что площадь каждой полоски, на которые разбивается криволинейная трапеция, заменяется площадью трапеции (рис. 8). В результате получается следующая формула трапеций численного интегрирования:

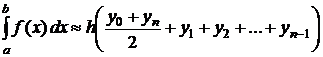(6.7)

Предельная погрешность этой формулы

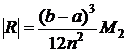(6.8)

где 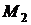– наибольшее значение 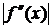на отрезке 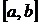. Таким образом, формула трапеций (как и формула прямоугольников) имеет погрешность порядка 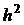относительно шага сетки 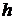и стремится к нулю при .

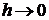Формула Симпсона (параболических трапеций). Подынтегральная кривая 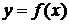заменяется на каждом 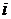-ом шаге параболой —интерполяционным многочленом Лагранжа второй степени 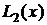(формула (4.3)), 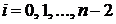. На равномерной сетке и четном количестве интервалов 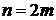деления отрезка интегрирования 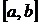получается формула Симпсона (парабол) приближенного вычисления интеграла:

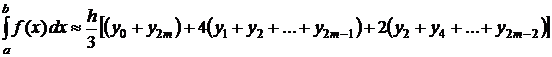. (6.9)

При одном и том же количестве интервалов деления отрезка интегрирования 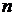формула Симпсона в большинстве случаев значительно точнее, чем формулы прямоугольников и трапеций. Ее предельная погрешность составляет

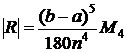, (6.10)

где 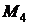– наибольшее значение 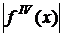на отрезке .

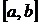П р и м е р 1. Применим формулу Симпсона к вычислению интеграла

.

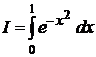• Четвертая производная для подынтегральной функции 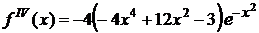. Ее абсолютное значение на отрезке интегрирования 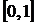не превосходит 12. Поэтому для погрешности получаем

.

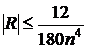Возьмем 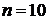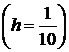. Это гарантирует погрешность, не превосходящую 0,000007. Вычисляем значения подынтегральной функции 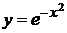с точностью до 0.000005 и оформляем их в табличном виде.

Таблица значений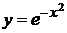

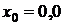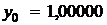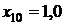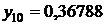сумма	1,36788
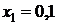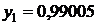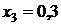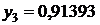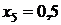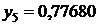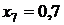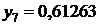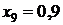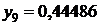сумма	3,74027
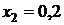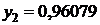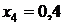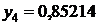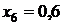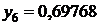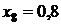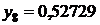сумма	3,03790

Используя табличные данные, получаем:

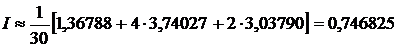
Погрешность при округлении вычисленных значений функции не превосходит величины

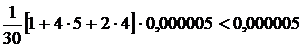
(при вычислении каждого значения 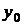, , 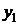… совершается ошибка до 0,000005, которая при сложении и вычитании может возрасти в соответствующее число раз; при делении возможная погрешность соответственно уменьшается). Следовательно, общая погрешность — формулы (6.9) и от округления значений функции — не превосходит величины 0,000012, так что

•

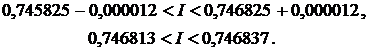Формулы численного интегрирования Гаусса и Чебышева. Квадратурные формулы численного интегрирования Гаусса и Чебышева применяют в тех случаях, когда требуется большая точность значения интеграла, но получение значений подынтегральной функции при большом числе значений аргумента по каким-либо причинам оказывается затруднительным.

Интеграл 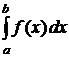с помощью замены переменной интегрирования

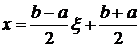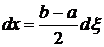, , (6.11)

приводится сначала к виду .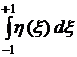

Квадратурная формула Гаусса:

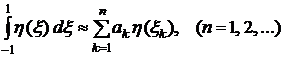. (6.12)

Абсциссы 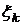и веса 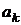для некоторых значений 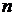приведены в таблице:

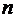	Абсциссы	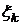Веса	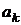	Абсциссы	Веса
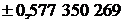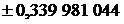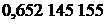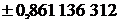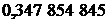		8/9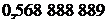
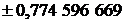		5/9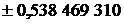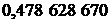

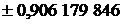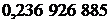Предельная погрешность квадратурной формулы Гаусса равна

.

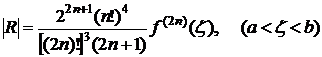Квадратурные формулы Чебышева применяются тоже после предварительной замены переменной (6.11); они имеют вид

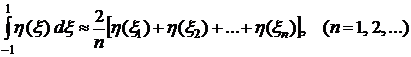. (6.12)

Абсциссы 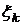для некоторых значений 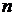приведены в таблице:

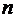	Абсциссы	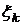	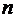Абсциссы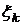

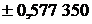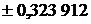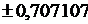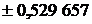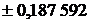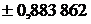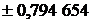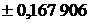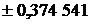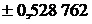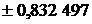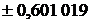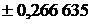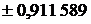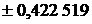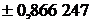Применение равных весов будет минимизировать случайную погрешность в тех случаях, когда значения 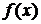получены в результате измерений и подвержены нормально распределенным случайным ошибкам.

П р и м е р 2. Вычислить по формуле Гаусса приближенное значение интеграла

,

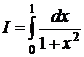взяв .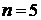

• Заменой 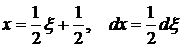преобразуем интеграл к промежутку 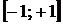. Получим:

, .

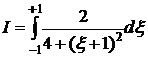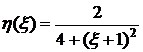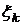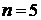Используя табличные значения абсцисс для , вычисляем :

, , ,

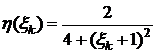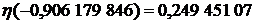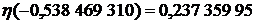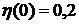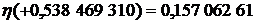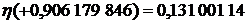, . Взяв из той же таблицы соответствующие веса 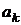, будем иметь:

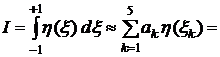
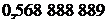·0,2+ ·( + )+ ·( + )= .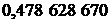

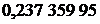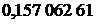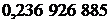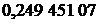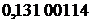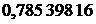Рассмотренный здесь интеграл вычисляется точно, и его значение равно 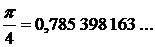Сравнивая, делаем вывод, что в вычисленном приближенном значении интеграла все знаки верны, т. е. формула Гаусса дает большую точность результата. Вместе с тем обращает на себя внимание то, что абсциссы 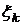и веса 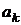очень громоздки.

3. Численное дифференцирование

Постановка задачи

При решении практических задач часто требуется найти производные указанных порядков от функции 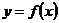, заданной таблично, или, в силу сложности аналитического выражения функции 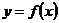, непосредственное ее дифференцирование затруднено. В этих случаях прибегают к приближенному дифференцированию.

Для этого на отрезке 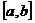функцию 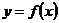заменяют интерполирующей функцией 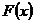(чаще всего интерполирующим полиномом 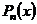), затем полагают 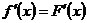при 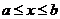. Аналогично поступают при нахождении производных высших порядков от функции .

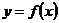Если для интерполирующей функции известна погрешность

,

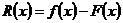то погрешность производной

,

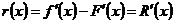т.е. погрешность производной интерполирующей функции равна производной от погрешности этой функции. То же справедливо для производных высших порядков.

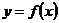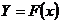Приближенное дифференцирование является менее точной операцией, чем интерполирование. Близость друг к другу ординат двух кривых и на отрезке 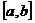еще не гарантирует близости на этом отрезке их производных 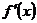и 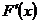, то есть малого расхождения угловых коэффициентов касательных к рассматриваемым кривым при одинаковых значениях аргумента.

Формулы приближенного дифференцирования, основанные на первой интерполяционной формуле Ньютона

Пусть на отрезке 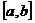заданы равноотстоящие точки 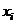: 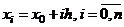, , 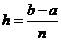и известны значения функции в этих точках 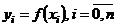. Требуется найти производные 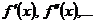на отрезке 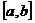(заранее известно, что эти производные существуют).

Заменим функцию 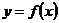интерполяционным полиномом Ньютона, построенным для узлов 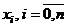, воспользовавшись первой интерполяционной формулой Ньютона:

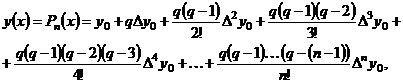(6.1)

где .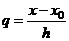

Произведя перемножение биномов и приведя подобные, получим:

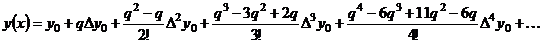(6.2)

Так как

,

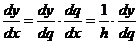то

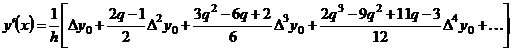(6.3)

Аналогично, так как

,

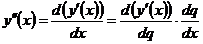то

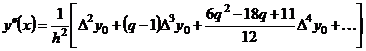. (6.4)

Таким образом можно вычислить производную любого порядка.

При нахождении производных в фиксированной точке в качестве 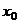следует брать ближайшее к 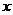табличное значение аргумента.

Формулы (6.3) и (6.4) упрощаются, если нужно подсчитать производные в узлах интерполяции. Полагая 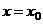, , 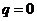получаем:

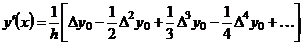, (6.5)

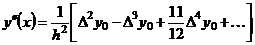. (6.6)

Пусть 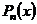- интерполяционный полином Ньютона, содержащий конечные разност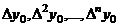и и 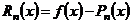, тогда 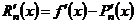. Но 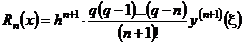. Тогда, если 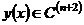, то

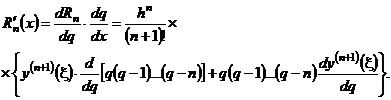(6.7)

Полагая 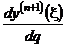- ограниченной и учитывая, что 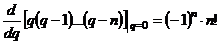, получаем при , :

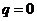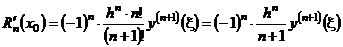. (6.8)

Так как 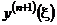сложно определить, то при малом шаге 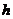принято считать 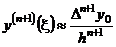. Тогда (6.8) примет вид:

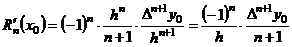. (6.9)

Аналогично находится 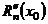и так далее.