Тема 21 Итерационные методы решения нелинейных уравнений и их систем

Лекция 21.1 «Итерационные методы решения нелинейных уравнений и их систем»

Учебные вопросы:

1. Введение. Отделение корней

2. Итерационные методы вычисления корней

3. Непрерывные схемы решения нелинейных уравнений

4. Итерационные методы решения систем нелинейных уравнений

Введение. Отделение корней

Введение. Если алгебраические уравнения второй степени (квадратные) решали уже древние греки, то способы решения алгебраических уравнений третьей и четвертой степени были найдены лишь в XVI в. Эти классические способы дают точные формулы решений этих уравнений через их коэффициенты при помощи корней различных степеней (радикалов). Однако эти формулы уже для уравнений третьей степени в общем случае достаточно сложны для вычислений, а для уравнений четвертого порядка требуют настолько громоздких вычислений, что теряют всякую практическую ценность.

В отношении алгебраических уравнений пятой и более высоких степеней доказано, что в общем случае их решения не выражаются через коэффициенты при помощи радикалов. Не выражаются в радикалах, например, корни уже такого простого по виду уравнения, как

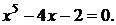
Сказанное, однако, не означает, что эти уравнения не могут быть решены. В настоящее время в вычислительной математике разработано достаточно много методов численного решения уравнений – алгебраических и неалгебраических (или, как их называют, трансцендентных), позволяющих находить их корни с любой, наперед заданной точностью, что, собственно, и требуется для практических целей. Более того, иногда бывает целесообразнее применить один из этих методов даже в том случае, если корни уравнения выражаются точной формулой, но вычисления по этой формуле трудоемки и/или оценка погрешности этих вычислений затруднена.

В этом параграфе будут приведены сведения о некоторых методах численного нахождения действительных корней уравнений

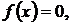(3.1)

где 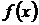– заданная функция действительного аргумента . В частности, для действительных алгебраических уравнений 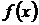представляет собой многочлен степени :

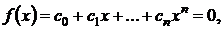(3.2)

где все его коэффициенты 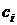– действительные числа.

При отыскании приближенных значений корней уравнения приходится решать две задачи:

1. отделение корней, т. е. отыскание достаточно малых промежутков, в каждом из которых заключен один и только один корень уравнения;

2. вычисление корней с заданной точностью.

3.2. Отделение корней. В общем случае процесс отделения корней уравнения не может быть алгоритмизирован. Для некоторых типов уравнений (в частности, алгебраических) разработаны специальные приемы отделения корней, позволяющие автоматизировать этот процесс.

Нередко отделение корней уравнений выполняется «вручную» с использованием всей возможной информации о функции 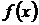. Для 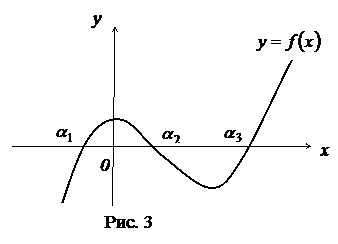отыскания грубых значений корней можно построить график функции 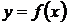и найти абсциссы точек пересечения графика с осью , которые затем можно взять за начальные приближения корней 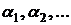(рис. 3). При отделении корней графическим способом иногда бывает полезным представить сначала уравнение (1) в эквивалентном виде 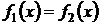и искать точки пересечения графиков функци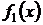й и 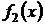. 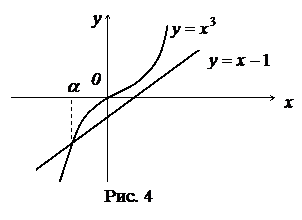Например, для уравнения 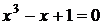вместо построения графика функции 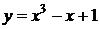проще построить графики функци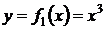й и 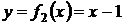(рис. 4).

Для выделения интервалов, в которых находятся корни уравнения 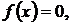если 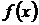– непрерывная функция, можно воспользоваться следующими предложениями:

· Если на концах некоторого отрезка 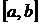непрерывная функция 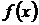принимает значения разных знаков, то на этом отрезке уравнение 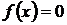имеет хотя бы один корень.

· Если при этом 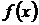имеет первую производную, не меняющую знака на этом отрезке (т. е. функция на отрезке либо нигде не убывает, либо не возрастает), то корень единственный.

· Если на концах отрезка 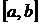непрерывная функция 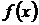принимает значения разных знаков, то между 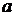и 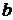имеется нечетное число корней уравнения 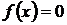; если же на концах отрезка 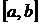она принимает значения одинаковых знаков, то между 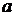и 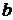или нет корней этого уравнения, или их имеется четное число (учитывая и кратность корней).

Для алгебраических уравнений (3.2) разработаны специальные методы и приемы отделения корней. Как известно, алгебраическое уравнение степени имеет ровно корней, если корень кратности 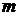считать 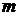раз (основная теорема алгебры многочленов). Эти корни могут быть как действительными, так и комплексными (выражаться через комплексные числа). Ограничиваясь только действительными корнями, необходимо предварительно определить их число. Для уравнений четных степеней действительных корней может и не быть, но действительные алгебраические уравнения нечетной степени всегда имеют хотя бы один действительный корень.

Найти границы области, в которой расположены все корни 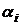(в том числе и комплексные) алгебраического уравнения (3.2), можно при помощи следующих теорем:

Т е о р е м а 1. Все корни уравнения (2) удовлетворяют неравенствам

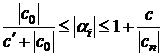, (3.3)

где 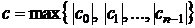, а .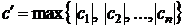

Т е о р е м а 2. Пусть в действительном алгебраическом уравнении коэффициент 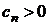(это всегда можно сделать). Обозначим через 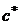максимум абсолютных величин отрицательных коэффициентов уравнения и пусть первый отрицательный коэффициент в ряду 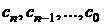есть 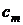. Тогда все положительные корни уравнения меньш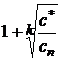е , где 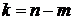(если же отрицательных коэффициентов нет, то нет и положительных корней). Применяя эту теорему к уравнению, в котором произведена замена на 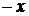, можно таким же образом получить нижнюю границу отрицательных корней.