Итерационные методы решения систем нелинейных уравнений.

Метод Ньютона для уравнений и систем. Метод бисекций для скалярного уравнения.

Методы Рунге-Кутта решения систем обыкновенных дифференциальных уравнений (ОДУ).

Разностные схемы для систем ОДУ. Устойчивость схем Рунге-Кутта.

Методы Рунге-Кутта ,семейство численных решения обыкновенных дифференциальных уравнений и их систем. обладают следующими свойствами:

1. Эти методы являются одноступенчатыми: чтобы найти уm+1, нужна

информация о предыдущей точке xm, ym.

2. Они согласуются с рядом Тейлора вплоть до членов порядка hp, где степень р

различна для различных методов и называется порядковым номером или

порядком метода.

3. Они не требуют вычисления производных от f (x, y), а требуют вычисления

самой функции.

R₁=f(x_m, y_m),

R₂=f(x_m+h/2, y_m+hR₁/2),

R₃=f(x_m+h/2, y_m+hR₂/2),

R₄=f(x_m+h/2, y_m+hR₃/2).

y_m+1=y_m+h/6(R₁+2R₂+2R₃+R₄)

Явные методы Рунге — Кутты

Семейство прямых методов Рунге — Кутты является обобщением метода Рунге — Кутты четвёртого порядка. Оно задаётся формулами

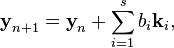
где 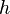— величина шага сетки по 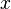и вычисление нового значения проходит в этапов:

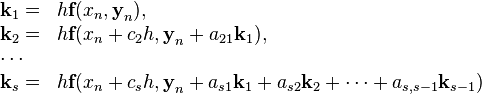
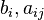Конкретный метод определяется числом и коэффициентами и 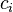. Эти коэффициенты часто упорядочивают в таблицу (называемую таблицей Бутчера)

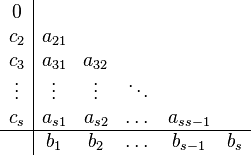
Для коэффициентов метода Рунге — Кутты должны быть выполнены услови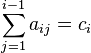я для 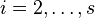. Если требуется, чтобы метод имел порядок 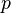, то следует также обеспечить условие

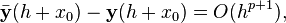
где 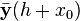— приближение, полученное по методу Рунге — Кутты. После многократного дифференцирования это условие преобразуется в систему полиномиальных уравнений относительно коэффициентов метода.

Неявные методы Рунге-Кутты

Все до сих пор упомянутые методы Рунге-Кутты являются явными методами. К сожалению, явные методы Рунге-Кутты, как правило, непригодны для решения жестких уравнений, из-за малой области абсолютной устойчивости. В частности, это описано в .Неустойчивость метода создаёт наибольшие проблемы при решении дифференциальных уравнений в частных производных.

Нестабильность явных методов Рунге-Кутты мотивировало развитие неявных методов. Неявный метод Рунге-Кутты имеет вид

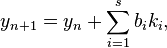
где

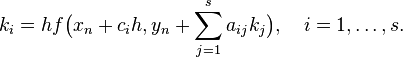
Явный метод характерен тем, что матрица коэффициентов 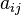для него имеет нижний треугольный вид, в отличие от неявного метода, где матрица имеет произвольный вид. Это также видно по таблице Бутчера.

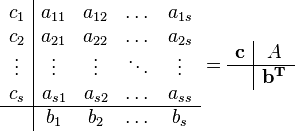
Следствием этого различия является необходимость на каждом шагу решать систему уравнений для 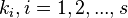, где число стадий. Это увеличивает вычислительные затраты, однако при достаточно малом 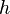эту систему можно представить в виде сжимающего отображения и решать методом простой итерации.. В случае одной итерации это увеличивает вычислительные затраты всего лишь в два раза.

С другой стороны, Ж. Кунцман (1961) и Дж. Бутчер (1964) показали, что при любом количестве стадий существует неявный метод с порядком точности 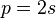. Это значит, что для описанного выше явного четырехстадийного метода четвёртого порядка существует неявный аналог с вдвое большим порядком точности.

Устойчивость

Преимуществом неявных методов Рунге-Кутты в сравнении с явными является их большая устойчивость, что особенно важно при решении жестких уравнений. Рассмотрим в качестве примера линейное уравнение y' = λy. Обычный метод Рунге-Кутты, примененный к этому уравнению сведется к итерации 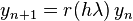, с r равным

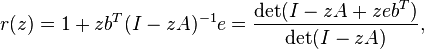
где e обозначает вектор единиц. Функция r называется функцией устойчивости Из формулы видно, что r является отношение двух полиномов степениs, если метод имеет s стадий. Явные методы имеют строго нижнюю треугольную матрицу A , откуда следует, что det(I − zA) = 1, и что функция устойчивости является многочленом.

Численное решение данного примера дает чистый ноль при условии | r(z) | < 1 с z = hλ. Множество таких r называется областью абсолютной устойчивости. В частности , метод называется A-стабильным если все r с Re(z) < 0 находятся в области абсолютной стабильности. Функция устойчивости явного метода Рунге-Кутта является многочленом, поэтому явные методы Рунге-Кутты в принципе не могут быть стабильными.

Если метод имеет порядок p, то функция стабильности удовлетворяет условию 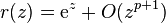при 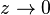. Таким образом, представляет интерес отношение многочленов данной степени, приближающее экспоненциальную функцию наилучшим образом. Эти отношения известны как аппроксимации Паде. Аппроксимация Паде с числителем степени m и знаменателем степени n А-устойчива, тогда и только тогда, когда m ≤ n ≤ m + 2.

s-стадийный метод Гаусса - Лежандра с имеет порядок 2s, поэтому его функция устойчивости является приближением Паде m = n = s. Отсюда следует, что метод является A-устойчивым. Это показывает, что A-устойчивые методы Рунге-Кутты могут иметь сколь угодно высокий порядок. В отличие от этого, порядок А-устойчивости метода Адамса не может превышать два.

Численное интегрирование.

Простейшие квадратурные формулы: прямоугольников,трапеций, парабол. Квадратурные формулы интерполяционного типа. Квадратурные формулы Гаусса. Погрешности квадратурных формул..