Тема 20 Учет погрешностей при вычислениях

Лекция 20.1 «Учет погрешностей при вычислениях»

Учебные вопросы:

1. Численные методы

2. Действия с приближенными величинами

Численные методы

Численные методы в математике – это методы решения математических задач, сводящиеся к выполнению конечного числа элементарных операций над числами (арифметических действий, выполняемых обычно приближенно, а также вспомогательных операций – записей промежуточных результатов, выборок из таблиц и т. п.). К таким математическим задачам относятся, например, задачи, для которых невозможно получить точного решения классическими методами или же решение может быть получено в таком сложном виде, который совершенно неприемлем для практического использования. Сюда же относятся задачи доведения до конкретного числового результата решений основных практически важных задач математического анализа, алгебры, геометрии и т. д., полученных в виде общих формул. Так, например, решение некоторого уравнения может привести к формуле корней через коэффициенты и параметры этого уравнения, в то время как на практике результат решения необходим в виде конкретного числа с определенной точностью. В таких случаях часто бывает рациональнее сразу воспользоваться каким-либо численным методом приближенных решений уравнений, чем точной формулой (тем более что на практике коэффициенты и параметры уравнений определяются, как правило, с конечной точностью).

Раздел вычислительной математики, называемый численными методами, называют также методами приближенных вычислений. К другому основному разделу вычислительной математики – теории программирования, относятся вопросы вычислительных алгоритмов (вычислительных схем при ручном счете) и составления программ для компьютерной реализации численных методов, а также сам процесс счета. В настоящее время существуют пакеты прикладных программ, такие как MathCAD, Matlab, Maple, Mathematica и другие, позволяющие находить численные решения многих частных математических задач.

Круг задач, с которыми приходиться сталкиваться в вычислительной математике, очень широк. Разнообразны и методы, применяемые для решения этих задач. Однако в этих методах прослеживается одна общая идея, которую можно отчетливее всего выразить в терминах функционального анализа.

Функциональные метрические пространства. Основным предметом исследования в классическом математическом анализе являются числовые функции и их системы, заданные на некотором множестве точек - мерного евклидова пространства.

В настоящее время в математике важную роль играют понятия о функциональном множестве, о функциональных пространствах и о функциональных операторах, т. е. о функциях, аргументами которых также являются элементы функциональных пространств. Вместо евклидовых пространств рассматриваются абстрактные пространства, элементы которых могут иметь самую различную природу. Так, например, введено понятие метрического пространства 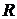как абстрактного множества, для любых двух элементов и которого определено понятие расстояния , удовлетворяющее следующим условиям:

1. 0, причем = 0 тогда и только тогда, когда совпадает с ;

2. = ;

3. + для любых трех элементов , , , 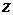принадлежащих 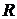(аксиома треугольника).

Евклидовы пространства, в которых определено обычное расстояние между точками, удовлетворяют всем этим условиям. Но определены и другие метрические пространства. Так, функциональное метрическое пространство С представляет собой множество всевозможных непрерывных функций, заданных на отрезке 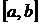. Расстояние для любых двух таких функций и определяется равенством

. (1.1)

Так определенное расстояние удовлетворяет всем трем приведенным выше условиям.

Другим важным классом функциональных пространств являются пространства (здесь 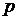- действительное число ). Расстояние в определено следующим образом:

. (1.2)

Определенное таким образом расстояние также удовлетворяет трем вышеприведенным условиям.

В каждом метрическом пространстве можно говорить об окрестности данной точки. - окрестностью точки некоторого метрического пространства 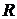называется совокупность его точек , для которых выполняется неравенство:

. (1.3)

В пространстве С это будет совокупность всех непрерывных на 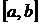функций, лежащих в полосе (рис. 1). В пространстве это будет

совокупность всех функций, принадлежащих , для которых

. (1.4)

При этом в отдельных точках отклонение от может быть очень большим, а зато в других точках будет очень малым (рис. 2).

В вычислительной математике часто приходится заменять одну функцию другой функцией, более удобной для вычислительных целей и в каком-то смысле близкой к первой. Обычно эту вторую функцию берут в некоторой - окрестности первой. Если - окрестность берется в пространстве С, то говорят о равномерном приближении функции . Если - окрестность берут в пространстве , то говорят о приближении в среднем. В частности, при p= 2 (пространство ) говорят о среднеквадратичном приближении.

Функции, определенные на функциональных пространствах. Как и в классическом математическом анализе, введено понятие функции, аргументом и значением которой являются элементы абстрактных пространств.

Пусть даны два абстрактных пространства и . Пусть каждому элементу поставлен в соответствие элемент . Тогда говорят, что задана функция

(1.5)

с областью определения и областью значений, принадлежащей . В частности, если является областью действительных или комплексных чисел, то называется функционалом. Простейшим примером функционала в пространстве С является

. (1.6)

Пространство может совпадать с пространством и тогда называют оператором. Область математики, изучающая свойства функциональных пространств и заданных на них функций, носит название функционального анализа.

Основной метод вычислительной математики. В вычислительной математике приходится сталкиваться с самыми различными задачами. Но большинство этих задач может быть записано в виде

, (1.7)

где и принадлежат заданным пространствам и и - некоторая заданная функция. Задача состоит либо в отыскании по заданному , либо в отыскании по заданному . Далеко не всегда с помощью средств современной математики удается точно решить эти задачи, применяя конечное число шагов. Иногда задача и может быть решена точно, но методы классической математики дают ответ после очень громоздких и трудоемких вычислений. Поэтому в задачи вычислительной математики входит также разработка приемов и методов наиболее рационального решения конкретных задач.

Основным методом, при помощи которого в вычислительной математике решают поставленные выше задачи, является замена пространств и и функции некоторыми другими пространствами и и функцией 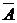, более удобными для вычислительных целей. Иногда бывает достаточно произвести замену пространств и или даже одного из них. Иногда достаточно заменить только функцию . Замена должна быть сделана так, чтобы решение новой задачи

, (1.8)

, - было в каком-то смысле близким к точному решению исходной задачи (1.7) и его возможно было бы практически отыскать со сравнительно небольшими вычислительными трудностями.

Например, пусть необходимо вычислить интеграл

,

где - непрерывная функция, причем неопределенный интеграл не берется в элементарных функциях. Чтобы получить приближенное значение интеграла с достаточной точностью, можно идти двумя путями.

1. Функцию можно заменить алгебраическим многочленом (т. е. многочленом вида ), равномерно приближающим функцию на отрезке 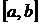с необходимой степенью точности. Это всегда можно сделать. Вместо интеграла необходимо будет уже находить интеграл , вычисление которого не составляет труда. Здесь, не меняя функционала , заменяется пространство С, которому принадлежит , пространством многочленов и вместо функции берется многочлен из некоторой ее - окрестности.

2. Из определения интеграла 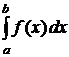следует, что всегда можно построить интегральную сумму , которая будет достаточно близка к значению интеграла. Следовательно, вместо вычисления интеграла можно решать другую задачу – задачу вычисления конечной суммы . Здесь уже производится замена функции новой функцией .