Необходимые условия экстремума

Теорема. В точке экстремума функции нескольких переменных каждая ее частная производная либо равна нулю, либо не существует.

Как и для функции одной переменной, точки, в которых

f'_x(x₀, y₀) = f'_y(x₀, y₀)=0 или не существуют, называются точками возможного экстремума или критическими точками функции. В этих точках экстремума может и не быть.

Достаточные условия экстремума функции z = f (x, y)

Теорема. Пусть функция f (x, y) определена и имеет непрерывные частные производные второго порядка в некоторой окрестности точки (x₀, y₀), в которой f'_x = f'_y = 0. Если при этом в этой точке выполнено условие

D = f''_xx × f''_yy – (f''_xy)²> 0, то точка (x₀, y₀) является точкой экстремума, причем точкой максимума, если f''_xx < 0, и точкой минимума, если f''_xx > 0.

Если же в этой точке f''_xx × f''_yy – (f''_xy)² < 0, то экстремума в точке (x₀, y₀) нет.

В том случае, если f''_xx × f''_yy – (f''_xy)² = 0 в точке (x₀,y₀), теорема ответа не дает.

Пример. Исследовать на экстремумы функцию z = xy + +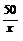

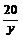
(x>0, y>0).

◄ Найдем точки возможного экстремума функции, для чего вычислим ее частные производные первого порядка и приравняем их к нулю.

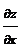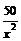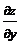= у – , = x – 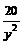. Решим систему 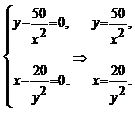. Подставим x = 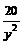в первое уравнение. Тогда получим y = 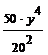= 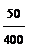y⁴ = 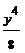. Имеем y = 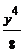. Далее 8y–y⁴=0, y(8–y³)=0 и y₁=0, y₂=2.

Находим значения x₁ и x₂, соответствующие этим значениям y.

x₁ при y₁=0 не существует. При у =2 x = 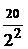= 5. Таким образом, точка возможного экстремума – M(5; 2).

Найдем вторые производные функции.

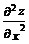= (y–50x^–2)'_x =2×50×x^–3 = ;

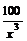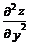= (x–20y^–2)'_y =2×20×y^–3 = ;

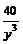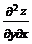= 1. Составим выражение D= 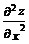× 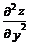– 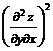и вычислим его значение в точке M(5; 2).

D= 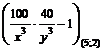= = 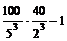= = 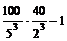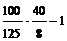4 – 1 > 0.

Экстремум есть. Так как в точке (5;2) 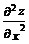= 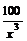> 0, то эта точка является точкой минимума функции. Вычислим значение в точке минимума:

z = 5×2 + 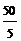+ 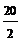=30. ►

Рассмотрим некоторое множество D точек плоскости (или пространства).

Определение. Наименьшее или наибольшее значение функции в данной области называется абсолютным экстремумом функции (абсолютным минимумом или абсолютным максимумом соответственно) в этой области.

Согласно теореме Вейерштрасса непрерывная в замкнутой ограниченной области функция достигает в ней своих наибольшего и наименьшего значений. Абсолютный экстремум достигается функцией либо в критических точках, либо на границе области.

Приведем алгоритм нахождения наибольшего и наименьшего значений:

1) находят все критические точки функции внутри области D и вычисляют значения функции в этих точках;

2) находят все точки наибольшего и наименьшего значений функции на границе области D;

3) среди найденных значений функции выбирают наибольшее и наименьшее.

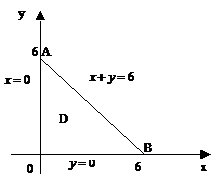
Пример. Найти наибольшее и наименьшее значения функции 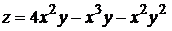в треугольнике, ограниченном прямыми 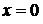, , 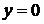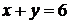(см. рис.).

◄ Найдем критические точки функции в области D.

.

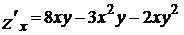
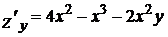Приравнивая производные 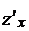и 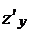к нулю, получим систему

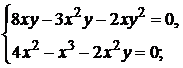
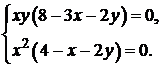
Из рисунка видно, что для внутренних точек области D выполнены условия 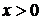, 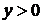. Тогда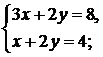 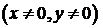. Вычитая из первого уравнения второе, получим 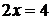, 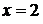. Подставляя 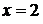во второе уравнение, получим 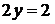, 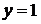. Получим точку 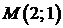. Очевидно, 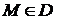, т. е. является критической. Вычислим значения 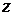в этой точке: .

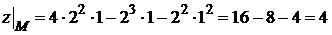Исследуем функцию на каждом из трех участков границы.

На участке ОА 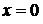. 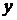здесь изменяется от значения 0 до значения 6, т.е. 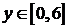. Подставляя в уравнение функции 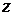уравнение ОА, получим 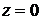. Это значение функции на всем отрезке ОА.

На промежутке ОВ 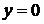и снова .

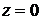На отрезке АВ 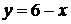, , 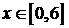а

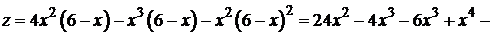
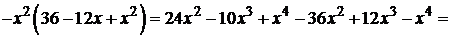
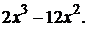
Итак, 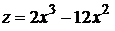, где .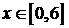

Найдем критические точки.

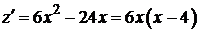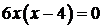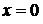, при и .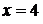

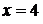– критическая точка, 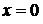– граничная. Найдем значения 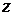в точках 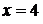, 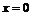и .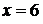

; ; .

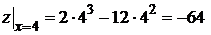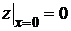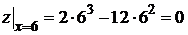Выбираем среди всех значений функции наибольшее и наименьшее: ; . ►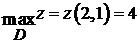

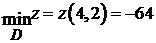Условный экстремум

Условный экстремум находится, когда переменные х и у, входящие в функцию u = f(x, y), не являются независимыми, т.е. существует некоторое соотношение f(х, у) = 0, которое называется уравнением связи. Тогда из переменных х и у только одна будет независимой, т.к. другая может быть выражена через нее из уравнения связи. Тогда u = f(x, y(x)) и

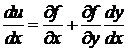. (1)

В точках экстремума:

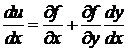=0.

Кроме того:

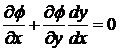. (2)

Умножим равенство (2) на число l и сложим с равенством (1):

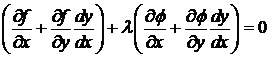или

.

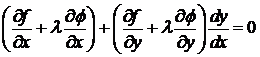Для выполнения последнего условия во всех точках найдем неопределенный коэффициент l так, чтобы выполнялась система трех уравнений:

.

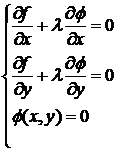Полученная система уравнений является необходимыми условиями условного экстремума. Однако это условие не является достаточным. Поэтому при нахождении критических точек требуется их дополнительное исследование на экстремум.

Выражение u = f(x, y) + lf(x, y) называется функцией Лагранжа.

Пример. Найти экстремум функции f(x, y) = xy, если уравнение связи:

2x + 3y – 5 = 0.

◄ Записываем функцию Лагранжа 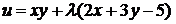. Находим ее частные производные: 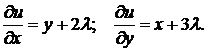Получаем систему уравнений:

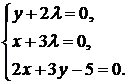
Решая систему, получим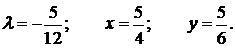

Таким образом, функция имеет экстремум . ►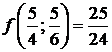

Использование функции Лагранжа для нахождения точек экстремума функции называется также методом множителей Лагранжа.

Выше мы рассмотрели функцию двух переменных, однако, все рассуждения относительно условного экстремума могут быть распространены на функции большего числа переменных.