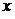Общая схема исследования функций и построения графиков

Общая схема исследования функций и построения их графиков:

1. Найти область определения функции.

2. Исследовать функцию на четность и нечетность.

3. Найти вертикальные асимптоты.

4. Исследовать поведение функции в бесконечности, найти горизонтальные и наклонные асимптоты.

5. Найти экстремумы и интервалы монотонности функции.

6. Найти интервал выпуклости функции и точки перегиба.

7. Найти точки пересечения с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.

Пример. Исследовать функцию 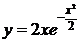и построить её график.

◄

1. Область определения .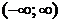

2. Функция нечетная, т.к. 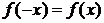, и график её симметричен относительно начала координат.

3. Вертикальных асимптот нет, т.к. функция определена при всех действительных x.

4. Поведение функции в бесконечности.

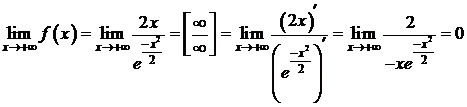
В силу нечетности функции, 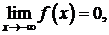т.е. прямая 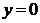(ось абсцисс) – горизонтальная асимптота.

5. Экстремумы и интервалы монотонности.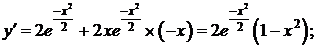

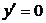при x=±1, т.е. критические точки .

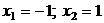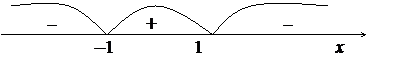Знаки производной изобразим на числовой оси :

Таким образом, 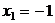– точка минимума, 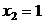– точка максимума.

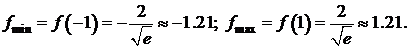
Функция убывает на 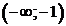и , и 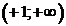возрастает на .

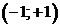6. Интервалы выпуклости и точки перегиба

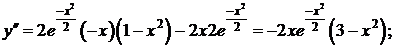
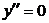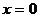при и .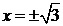

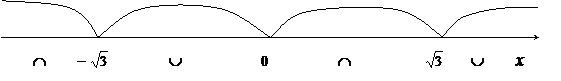Знаки 2-й производной изобразим на числовой прямой:

Функция выпукла вниз на интервалах 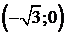и 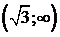, и выпукла вверх на 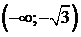и .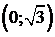

7. 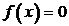имеет единственное решение 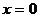. Это точка пересечения с осями координат.

График функции имеет вид:

►

Тема 10 Дифференциал функции

Лекция 10.1 «Дифференциал функции»

Учебные вопросы:

1. Дифференциал

2. Применение дифференциала в приближенных вычислениях

Дифференциал

Пусть функция 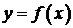определена на промежутке Xи дифференцируема в окрестности точки 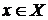. Тогда существует конечная производная 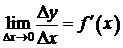. Отсюда 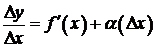, где 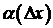бесконечно малая пр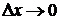и , или .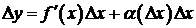

Таким образом, приращение функции 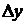состоит из двух слагаемых – линейного относительно 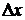и нелинейного, представляющего бесконечно малую более высокого порядка, чем .

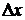Дифференциалом функции называется главная, линейная относительно 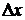часть приращения функции, равная произведению производной на приращение независимой переменной:

.

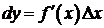Например, дифференциал функции 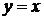равен 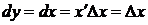, откуда 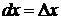. Поэтому формулу для дифференциала функции можно записать в виде:

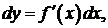откуда .

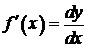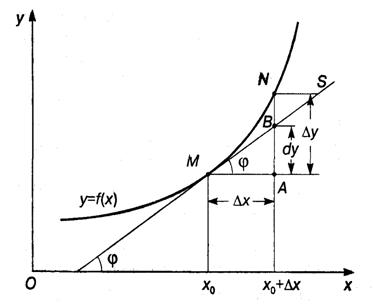
Геометрический смысл дифференциала: дифференциал равен приращению ординаты касательной, проведенной к графику функции 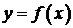в данной точке, когда xполучает приращение 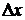(см. рис.).

Свойства дифференциала в основном аналогичны свойством производной:

1. .

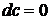2. .

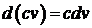3. .

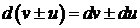4. .

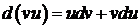5.

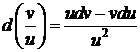
Рассмотрим сложную функцию 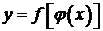. Если функци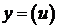и и 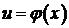– дифференцируемые функции своих аргументов, то производная сложной функции равна 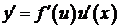. Тогда дифференциал функции 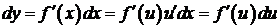.Таким образом, 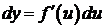. Это означает, что формула дифференциала не изменяется, если вместо функции от независимой переменной x рассмотреть функцию от зависимой переменной u. Это свойство дифференциала называется инвариантностью формы дифференциала.