Уравнения с одним неизвестным. Корень уравнения. Линейные уравнения
Уравнением называется равенство, содержащее неизвестные переменные.
Уравнение с одним неизвестным x записывается в виде f(x)=g(x).
Корнем уравнения называется всякое число, при подстановке которого вместо неизвестной в обе части уравнения получается верное числовое равенство.
Решить уравнение – значит найти все его корни, или доказать, что их нет.
Областью определения (ОО) уравнения или областью допустимых значений уравнения (ОДЗ) называется множество всех тех значений переменных x, при которых оба выражения f(x) и g(x) имеют смысл.
Два уравнения называются равносильными на данном числовом множестве, если они имеют одни и те же корни или оба не имеют корней.
Линейным уравнением с одним неизвестным называется уравнение вида ax + b = 0, где а и b – действительные числа, x – неизвестная величина.
При решении линейного уравнения возможны случаи:
· если а ≠ 0, то ax + b = 0, 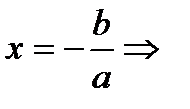 один корень;
один корень;
· если a = b = 0, то 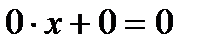 ,
, 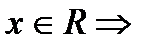 бесконечное множество решений;
бесконечное множество решений;
· если a = 0, b ≠ 0, то 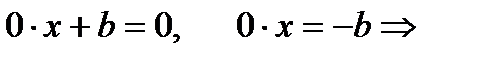 корней нет.
корней нет.
Квадратные уравнения. Теорема Виета
Уравнение вида 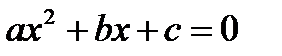 , где x – переменная, a, b, c – некоторые числа, причем, а ≠ 0, называется квадратным.
, где x – переменная, a, b, c – некоторые числа, причем, а ≠ 0, называется квадратным.
а – первый коэффициент;
b – второй коэффициент;
с – свободный член.
Квадратные уравнения, в которых хотя бы один из коэффициентов b или с равен нулю, называются неполными.
 | 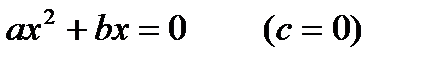 | 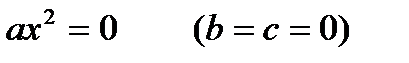 |
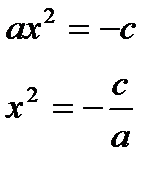 1) Если ас > 0 – корней нет 2) Если ac < 0 1) Если ас > 0 – корней нет 2) Если ac < 0 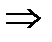 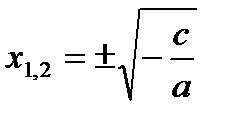 | 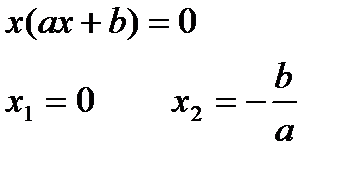 | x=0 |
Выведем формулу корней квадратного уравнения. Для этого решим уравнение 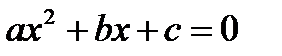 , где а ≠ 0. Разделим все его члены на а. Получим равносильное уравнение:
, где а ≠ 0. Разделим все его члены на а. Получим равносильное уравнение: 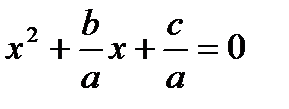 (2).
(2).
Выделим полный квадрат: 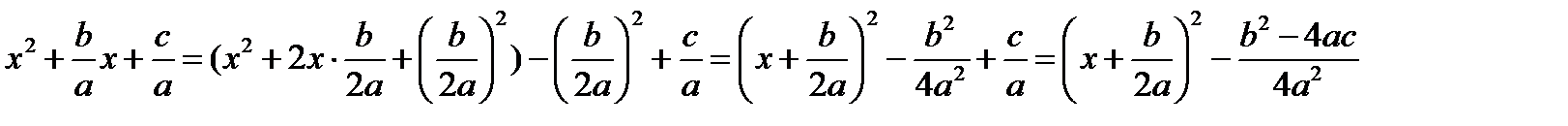 .
.
Тогда уравнение (2) примет вид 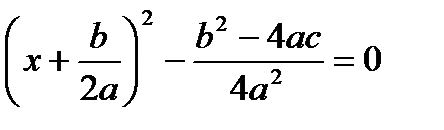
или 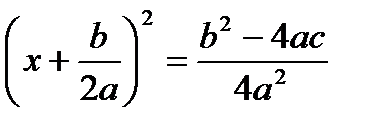 (3).
(3).
Число корней зависит от знака дроби 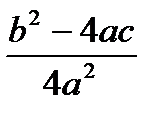 , т.к. а ≠ 0, то
, т.к. а ≠ 0, то 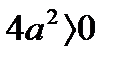
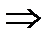 знак определяется выражением
знак определяется выражением 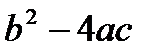 . Обозначим его D =
. Обозначим его D = 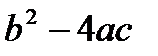 и назовем дискриминантом. Тогда уравнение (3) перепишется в виде:
и назовем дискриминантом. Тогда уравнение (3) перепишется в виде: 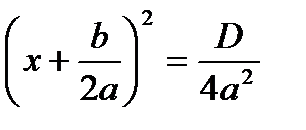 (4). Рассмотрим случаи:
(4). Рассмотрим случаи:
| D < 0 | D = 0 | D > 0 |
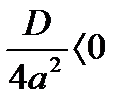 , но , но 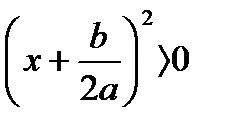 для любого действительного x. Значит, корней нет. для любого действительного x. Значит, корней нет. | 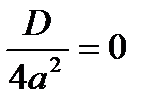 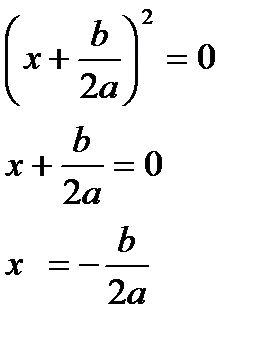 Значит, два равных корня Значит, два равных корня 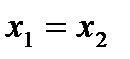 . . | 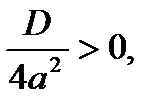 то то 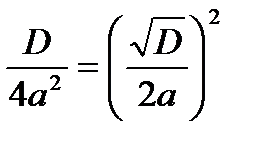 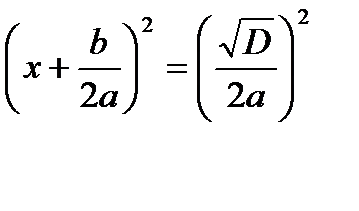 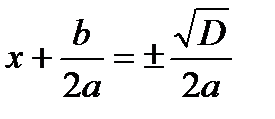 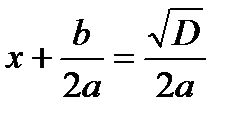 или или 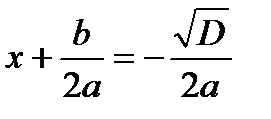 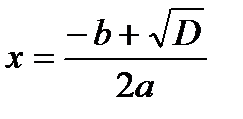 или или 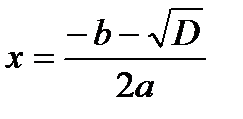 Значит, два различных корня Значит, два различных корня 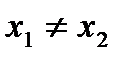 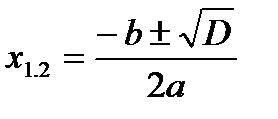 , где D = , где D = 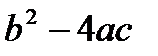 |
При решении квадратного уравнения, в котором второй коэффициент
b – четное число, используют следующую формулу:
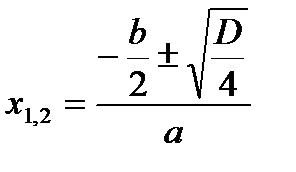 , где
, где 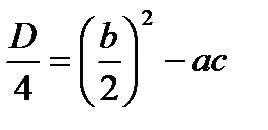 .
.
Квадратное уравнение, первый коэффициент которого равен 1, называется приведенным: 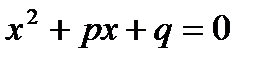 . Корни приведенного квадратного уравнения можно найти по формулам:
. Корни приведенного квадратного уравнения можно найти по формулам: 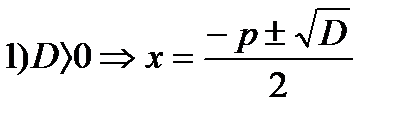 ;
;
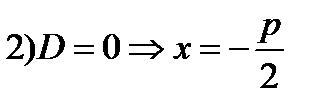 .
.
Теорема Виета: Сумма корней квадратного уравнения 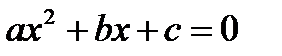 равна
равна 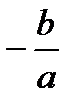 , произведение корней равно
, произведение корней равно 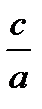 .
.
Доказательство:
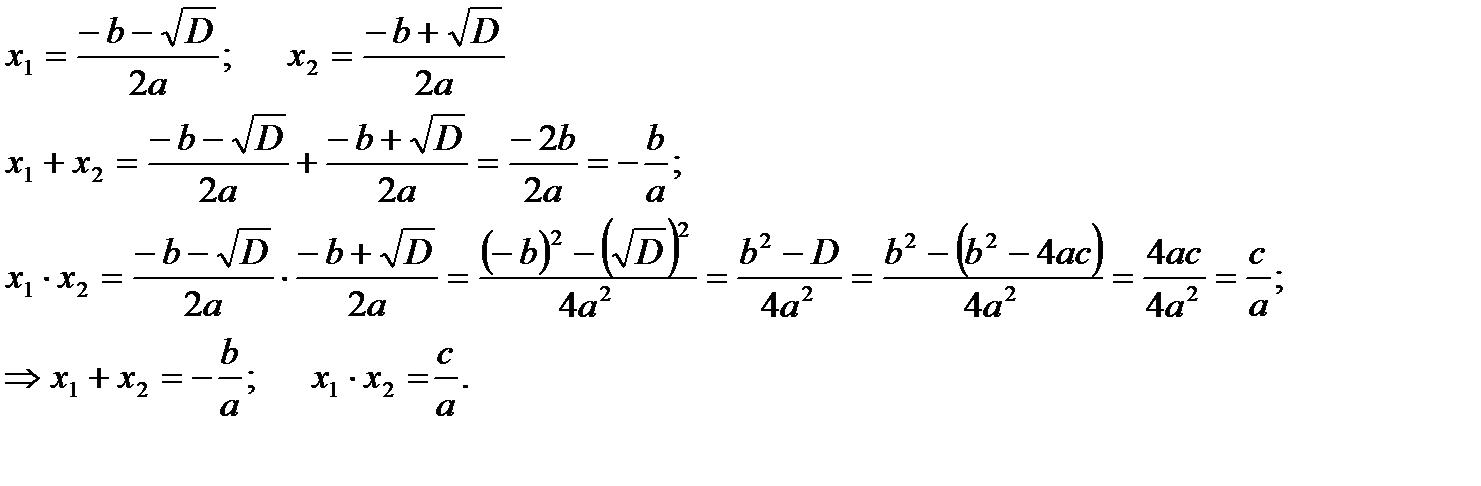
Теорема доказана.
Следствие: Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену: 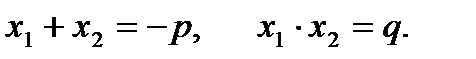
Обратная теорема: Если числа x1 и x2 такие, что 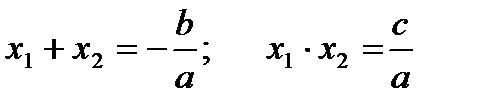 , то они являются корнями квадратного уравнения
, то они являются корнями квадратного уравнения 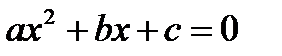 .
.
Определение знаков корней квадратного уравнения.
| Оба положительны | Оба отрицательны | Одного знака | Разных знаков |
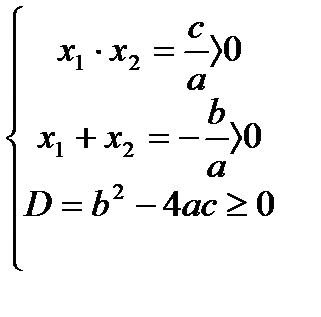 | 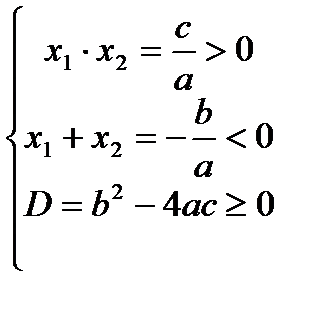 | 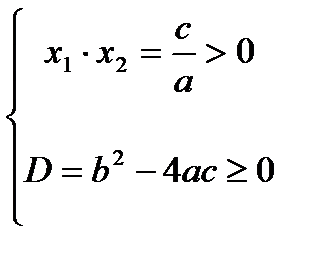 | 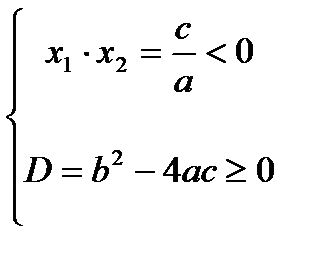 |
Уравнение 4-ой степени вида 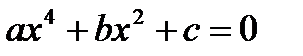 , где а ≠ 0, называется биквадратным.
, где а ≠ 0, называется биквадратным.
