Несмещённые оценки дисперсии ошибок, ковариационной матрицы и дисперсии выборочных коэффициентов регрессии

Несмещённая оценка дисперсии ошибок (несмещённая выборочная ос­таточная дисперсия) определяется выражением:

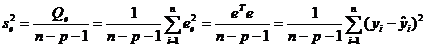. (13)

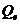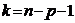Как видно из (13), несмещённая оценка дисперсии получается путём деления остаточной суммы квадратов на степеней свободы, по­скольку 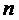- число наблюдений, а 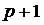степени свободы теряются при определе­нии коэффициентов 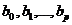уравнения регрессии.

Несмещённая оценка матрицы ковариации вектора коэффициентов b получается путём замены в (12) неизвестного значения дисперсии возмуще­ния 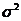его оценкой (13):

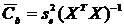, (14)

откуда следует, что несмещённые оценки дисперсий коэффициентов 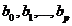находятся по формуле:

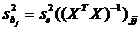, (15)

где 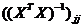- j-й диагональный элемент матрицы .

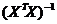Из формулы (15) вытекает выражение для стандартных отклонений оценок коэффициентов регрессии (несмещённых оценок средних квадратных отклонений ):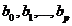

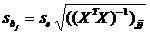. (16)

Оценка значимости и доверительных интервалов
для коэффициентов регрессии

Пусть 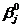- некоторое заданное гипотетическое значение 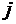-го коэффици­ента 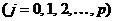. При оценке значимости коэффициентов регрес­сии 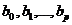формулируются следующие гипотезы:

Основная гипотеза .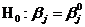

Конкурирующая гипотеза .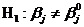

Статистикой критерия является случайная величина:

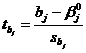, (17)

которая при условии выполнения гипотезы 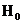имеет распределение Стью­дента (t-распределение) с 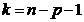степенями свободы.

Критическая область, как следует из вида гипотезы 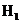, является двусто­ронней. Уровень значимости определяется выражением:

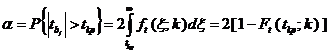, (18)

где 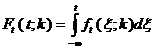- интегральная функция распределения вероятностей, а доверительный уровень находится по формуле:

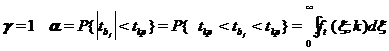. (19)

Критическая точка

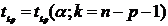(20)

находится по статистическим таблицам или с помощью стандартных функ­ций в пакетах прикладных программ.

При значении 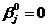статистика (17) сводится к виду:

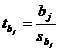, (21)

и гипотезы при оценке значимости элементов вектора b формируются сле­дующим образом.

Основная гипотеза 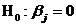принимается в случае, когда 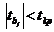, и с уровнем значимости 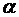делается вывод о том, что коэффициент 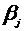незначим. Альтернативная гипотеза 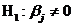применяется в том случае, когда 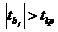, и с уровнем значимости 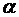делается вывод о том, что коэффициент 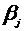значим.

Величина 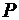-значения определяется по формуле:

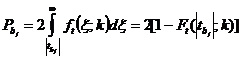. (22)

При этом выполнение неравенства 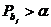означает, что 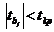, и принимается основная гипотеза 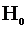. Если 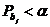, то 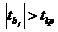, и принимается альтернативная гипотеза .

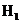Из выражений (17), (19) следует, что с доверительной вероятностью 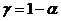истинное значение 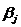коэффициента регрессии лежит в интервале:

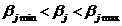, (23)

где 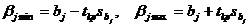- нижние и верхние g * 100%.

Анализ вариации зависимой переменной

Общая сумма квадратов отклонений 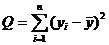разбивается на два слагаемых:

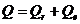, (24)

где 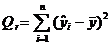, 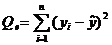- соответственно факторная и остаточная суммы квадратов.

По аналогии со случаем парной регрессии эти суммы можно выразить через вектор выборочных коэффициентов b и выборочный коэффициент детерминации (табл. 8):

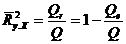
Значения сумм квадратов

Таблица 8

Название	Общее выражение	Выражение через b	Выражение через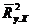
Общая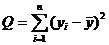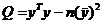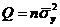
Факторная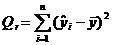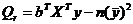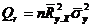
Остаточная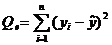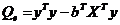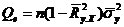

При делении суммы квадратов на число её степеней свободы получается несмещённая оценка соответствующей дисперсии (табл. 9).

Значения дисперсий

Таблица 9

Название		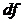Выражение
Общая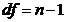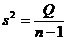
Факторная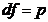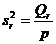
Остаточная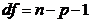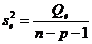