Обработка результатов многократных измерений одной и той же величины
Содержание
Введение....................................................................................................... 4
Лабораторная работа №1. Определение погрешностей результатов измерений 5
Лабораторная работа №2. Вычисление структурных
средних величин (СВ)................................................................................... 11
Корреляционно-регрессионный анализ......................................................... 12
Лабораторная работа №3. Модель парной регрессии................................... 15
Лабораторная работа №4. Проверка адекватности модели парной регрессии 18
Лабораторная работа №5. Множественная регрессионная модель. Классическая линейная модель 25
Лабораторная работа №6. Задачи оптимизации.......................................... 46
Лабораторная работа №7. Модель Леонтьева.............................................. 49
Лабораторная работа №8. Фильтрация списков........................................... 52
Библиографический список.......................................................................... 54
Приложение.................................................................................................. 55
Введение
Математические методы обработки информации уже давно применяются в самых разнообразных областях человеческой деятельности. Трудно назвать ту сферу общественно-политической жизни, в которой они бы не использовались. Но, пожалуй, ни в одной области знаний и практической деятельности обработка этой информации (так называемых статистических данных) не играет такой исключительно большой роли, как в экономике, имеющей дело с обработкой и анализом огромных массивов количественной информации о социально-экономических явлениях и процессах. Для достоверного отображения объективно существующих в экономике процессов необходимо выявить существенные взаимосвязи и не только выявить, но и дать им количественную оценку. Этот подход требует вскрытия причинных зависимостей, т.е. таких связей между процессами, когда изменения, происходящие в одном из них, являются следствием изменений, происходящих в другом. Всесторонний и глубокий анализ статистических данных предполагает использование различных специальных математических методов, важное место среди которых занимает корреляционно-регрессионный анализ.Основными задачами корреляционного анализа являются оценка силы связи и проверка статистических гипотез о наличии и силе корреляционной зависимости между введенными для изучения процесса переменными (факторами и результатом). Не все факторы, влияющие на экономические процессы, являются случайными величинами, поэтому при анализе экономических явлений обычно рассматриваются связи между случайными и неслучайными величинами. Такие связи называются регрессионными, а метод математической статистики, их изучающий - регрессионным анализом.Использование возможностей современной вычислительной техники, оснащенной пакетами программ машинной обработки информации, позволяет оперативно решать задачи изучения взаимосвязи показателей реальных процессов методами корреляционно-регрессионного анализа. При компьютерной обработке исходной информации вычисление параметров применяемых математических функций и анализ статистических зависимостей являются быстро выполняемыми счетными операциями.Корреляционно-регрессионный анализ считается одним из главных методов в экономике, наряду с оптимизационными расчетами, а также математическим и графическим моделированием трендов (тенденций).Данная работа предназначена для изучения возможностей обработки статистических данных различными методами (в том числе, методами корреляционного и регрессионного анализа) с использованием пакета прикладных программ Microsoft Excel.Лабораторная работа №1
Определение погрешностей результатов измерений
Лабораторная работа №3
Модель парной регрессии
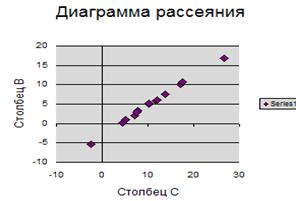
Используя исходные данные, построить модель парной регрессии для изучения зависимости х от у, построить диаграмму рассеяния.
Исходные данные представлены в таблице 7.
Таблица 7
| Номер наблюдения | х | у |
| -2,54 | -5,31 | |
| 26,65 | 16,84 | |
| 4,44 | 0,07 | |
| 17,12 | 10,03 | |
| 10,19 | 4,98 | |
| 13,88 | 7,52 | |
| 4,55 | 0,23 | |
| 10,28 | 5,3 | |
| 11,76 | 5,94 | |
| 11,89 | 6,09 | |
| 5,14 | 0,93 | |
| 7,7 | 3,22 | |
| 7,17 | 2,08 | |
| 7,57 | 2,81 | |
| 17,46 | 10,73 |
Ход работы
1. Находим средние значения 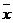 и
и 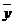 величин х и у средствами Microsoft Excel: с помощью мыши выделяем ячейку для искомого значения
величин х и у средствами Microsoft Excel: с помощью мыши выделяем ячейку для искомого значения 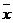 , выбираем значок fx на панели инструментов, затем находим функцию СРЗНАЧ в окне ниспадающего меню, нажимаем OK, в поле Число1 заносим столбец значений х с помощью мыши, нажимаем OK. Аналогично находим среднее значение величины y.
, выбираем значок fx на панели инструментов, затем находим функцию СРЗНАЧ в окне ниспадающего меню, нажимаем OK, в поле Число1 заносим столбец значений х с помощью мыши, нажимаем OK. Аналогично находим среднее значение величины y.
2. Находим значение 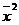 : выделяем ячейку для искомого значения, в выделенной ячейке ставим знак «=», щелкаем мышью по ячейке, содержащей значение
: выделяем ячейку для искомого значения, в выделенной ячейке ставим знак «=», щелкаем мышью по ячейке, содержащей значение 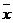 , ставим знак «*» , снова щелкаем мышью по ячейке, содержащей значение
, ставим знак «*» , снова щелкаем мышью по ячейке, содержащей значение 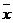 , нажимаем Enter.
, нажимаем Enter.
3. Находим величину 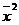 * t, где t - число элементов в выборке. Для этого выделяем ячейку для искомой величины, в выделенной ячейке ставим знак «=», щелкаем мышью по ячейке, содержащей значение
* t, где t - число элементов в выборке. Для этого выделяем ячейку для искомой величины, в выделенной ячейке ставим знак «=», щелкаем мышью по ячейке, содержащей значение 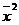 , ставим знак «*», заносим число 15 с клавиатуры, нажимаем Enter.
, ставим знак «*», заносим число 15 с клавиатуры, нажимаем Enter.
4. Находим произведение х*у: выделяем ячейку, в выделенной ячейке ставим знак «=», щелкаем мышью по ячейке, содержащей первое значение в выборке х, ставим знак «*», далее щелкаем мышью по ячейке, содержащей первое значение в выборке у, нажимаем Enter. Удерживая левую кнопку мыши, протягиваем вниз еще на 14 ячеек, получая тем самым произведения соответствующих значений х и у.
5. Находим сумму 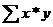 получившихся значений: щелкаем по ячейке, выше которой располагаются найденные в пункте 4 значения, ставим знак «=», выбираем значок ∑ (автосумма) на панели инструментов, далее выделяем с помощью мыши все получившиеся значения произведений, нажимаем Enter.
получившихся значений: щелкаем по ячейке, выше которой располагаются найденные в пункте 4 значения, ставим знак «=», выбираем значок ∑ (автосумма) на панели инструментов, далее выделяем с помощью мыши все получившиеся значения произведений, нажимаем Enter.
Находим произведение средних значений 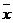 *
* 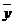 : выделяем ячейку, в выделенной ячейке ставим знак «=», щелкаем мышью по ячейке, содержащей значение
: выделяем ячейку, в выделенной ячейке ставим знак «=», щелкаем мышью по ячейке, содержащей значение 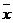 , ставим знак «*», щелкаем мышью по ячейке, содержащей значение
, ставим знак «*», щелкаем мышью по ячейке, содержащей значение 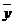 , нажимаем Enter.
, нажимаем Enter.
6. Умножаем результат, полученный в пункте 6, на количество элементов выборки, в нашем случае на 15, т.е. находим 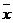 *
* 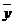 *t.
*t.
7. Находим 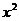 : выделяем одну ячейку, в выделенной ячейке ставим знак «=», щелкаем мышью по ячейке, содержащей первое значение в выборке х, ставим знак «*», снова щелкаем мышью по этой же ячейке, нажимаем Enter, удерживая левую кнопку мыши, протягиваем вниз еще на 14 ячеек.
: выделяем одну ячейку, в выделенной ячейке ставим знак «=», щелкаем мышью по ячейке, содержащей первое значение в выборке х, ставим знак «*», снова щелкаем мышью по этой же ячейке, нажимаем Enter, удерживая левую кнопку мыши, протягиваем вниз еще на 14 ячеек.
8. Находим сумму получившихся значений 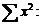 щелкаем по ячейке, выше которой располагаются найденные значения, ставим знак «=», выбираем значок ∑ (автосумма) на панели инструментов и выделяем с помощью мыши все получившиеся значения, нажимаем Enter.
щелкаем по ячейке, выше которой располагаются найденные значения, ставим знак «=», выбираем значок ∑ (автосумма) на панели инструментов и выделяем с помощью мыши все получившиеся значения, нажимаем Enter.
9. Находим коэффициенты а и b, используя формулы (1), (2)
b = 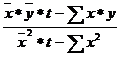 , (1)
, (1)
а = 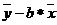 (2)
(2)
следующим образом: выделяем ячейку, ставим знак «=», щелкаем мышью по ячейке, содержащей значение, полученное в пункте 7, ставим знак «–», щелкаем мышью по ячейке, содержащей значение, полученное в пункте 5, заключаем в скобки данное выражение, ставим знак «/», щелкаем мышью по ячейке, содержащей значение, полученное в пункте 3, ставим знак «–», щелкаем мышью по ячейке, содержащей значение, полученное в пункте 9, заключаем в скобки, нажимаем Enter. Таким образом, мы получили коэффициент b.
Выделяем ячейку, в выделенной ячейке ставим знак «=», щелкаем мышью по ячейке, содержащей значение 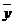 , ставим знак «–», щелкаем мышью по ячейке, содержащей значение коэффициента b, ставим знак «*», щелкаем мышью по ячейке, содержащей значение
, ставим знак «–», щелкаем мышью по ячейке, содержащей значение коэффициента b, ставим знак «*», щелкаем мышью по ячейке, содержащей значение 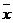 , нажимаем Enter. Получили коэффициент а.
, нажимаем Enter. Получили коэффициент а.
10. Строим диаграмму: выбираем значок мастера диаграмм на панели инструментов, выбираем точечную диаграмму, вид, расположенный в верхнем квадрате, нажимаем «Далее», в качестве диапазона данных заносим исходные значения х и у, выделяя их с помощью мыши, устанавливаем флажок «в столбцах», нажимаем «Далее» во всех следующих случаях, в конце построения нажимаем «Готово».
Пример оформления работы на листе Excel.
| t | х | у | х*у | 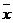 * * 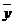 | 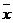 * * 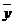 *t *t | 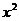 | ||
| -2,54 | -5,31 | 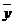 | 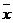 | 13,4874 | 48,6754 | 730,131 | 28,196 | |
| 26,65 | 16,84 | 10,21733 | 4,764 | 448,786 | 283,59 | |||
| 4,44 | 0,07 | 0,3108 | 0,0049 | |||||
| 17,12 | 10,03 | 171,7136 | 100,6 | |||||
| 10,19 | 4,98 |  | 50,7462 | 24,8 | ||||
| 13,88 | 7,52 | 22,6957 | 104,3776 | 56,55 | ||||
| 4,55 | 0,23 | 1,0465 | 0,0529 | |||||
| 10,28 | 5,3 | 54,484 | 28,09 | |||||
| 11,76 | 5,94 | 69,8544 | 35,284 | |||||
| 11,89 | 6,09 | 72,4101 | 37,088 | |||||
| 5,14 | 0,93 | 4,7802 | 0,8649 | |||||
| 7,7 | 3,22 | 24,794 | 10,368 | |||||
| 7,17 | 2,08 | 14,9136 | 4,3264 | |||||
| 7,57 | 2,81 | 21,2717 | 7,8961 | |||||
| 17,46 | 10,73 | 187,3458 | 115,13 | |||||
| Сумма | 1240,322 | Сумма | 732,84 | |||||
| b | 1,30016 | Модель парной регрессии y = 4,02 + 1,3*x | ||||||
| a | 4,02337 |
Лабораторная работа №4
Проверка адекватности модели парной регрессии
Задание
1. Вычислить коэффициент детерминации для полученной модели, используя различные формы представления коэффициента.
2. Проверить значимость коэффициента детерминации на основании
F-теста.
Основная формула:
Σ (yt - 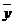 )2 = Σ (yэмп -
)2 = Σ (yэмп - 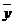 )2 + Σ (yt - yэмп)2 ,
)2 + Σ (yt - yэмп)2 ,
или
TSS = ESS + RSS ,
где TSS – полная сумма квадратов;
ESS - сумма квадратов, объясненная моделью;
RSS – остаточная сумма квадратов.
Ход работы
1. Находим эмпирическое значение yэмп величины y: выделяем ячейку, в выделенной ячейке ставим знак «=», щелкаем мышью по ячейке, содержащей значение а, ставим в строке формул знак «$» перед буквой и цифрой, чтобы зафиксировать значение, ставим знак «+», щелкаем мышью по ячейке, содержащей значение b, снова ставим в верхней строке формулы знак «$» перед буквой и перед цифрой, чтобы зафиксировать значение, нажимаем знак «*», щелкаем мышью по ячейке, содержащей значение x, нажимаемEnter. Удерживая левую кнопку мыши, протягиваем вниз, чтобы получилось 15 ячеек. Нашли 15 значений yэмп, соответствующие значениям х.
2. Находим ESS: выделяем одну ячейку, в выделенной ячейке ставим знак «=», открываем скобку, щелкаем мышью по ячейке, содержащей первое значение yэмп, ставим знак «-», далее щелкаем мышью по ячейке, содержащей среднее значение 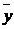 , фиксируем его в строке формул знаком «$» перед буквой и перед цифрой, закрываем скобку и умножаем на аналогичную скобку, так как нам нужен её квадрат, нажимаем Enter. Удерживая левую кнопку мыши, протягиваем вниз еще на 14 ячеек. Затем находим сумму получившихся значений: щелкаем по ячейке, находящейся ниже этих значений, ставим знак «=», выбираем значок ∑ (автосумма) на панели инструментов и выделяем с помощью мыши все получившиеся значения произведений, нажимаемEnter.
, фиксируем его в строке формул знаком «$» перед буквой и перед цифрой, закрываем скобку и умножаем на аналогичную скобку, так как нам нужен её квадрат, нажимаем Enter. Удерживая левую кнопку мыши, протягиваем вниз еще на 14 ячеек. Затем находим сумму получившихся значений: щелкаем по ячейке, находящейся ниже этих значений, ставим знак «=», выбираем значок ∑ (автосумма) на панели инструментов и выделяем с помощью мыши все получившиеся значения произведений, нажимаемEnter.
3. Находим TSS: делаем все то же самое, что и в пункте 2, только вычитаем среднее значение 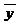 не от yэмп , а от y.
не от yэмп , а от y.
4. Находим RSS: выделяем 1 ячейку, в выделенной ячейке ставим знак «=», открываем скобку, щелкаем мышью по ячейке, содержащей первое значение y, ставим знак «-», далее щелкаем мышью по ячейке, содержащей значение yэмп, закрываем скобку и умножаем на аналогичную скобку, нажимаем Enter. Удерживая левую кнопку мыши, протягиваем вниз еще на 14 ячеек. Находим сумму получившихся значений: щелкаем по ячейке, находящейся ниже этих значений, ставим знак «=», выбираем значок ∑ (автосумма) на панели инструментов и выделяем с помощью мыши все получившиеся значения произведений, нажимаем Enter.
5. Находим коэффициент детерминации по первой формуле:
R2 = ESS/TSS.
Выделяем ячейку, ставим знак «=», щелкаем мышью по ячейке, содержащей значение суммы ESS, ставим знак «/», щелкаем мышью по ячейке, содержащей значение суммы TSS, нажимаем Enter.
6. Находим коэффициент детерминации по второй формуле:
R2 = 1- (RSS/TSS).
Выделяем ячейку, ставим знак «=», нажимаем 1, ставим знак «-», затем открываем скобку, щелкаем мышью по ячейке, содержащей значение суммы RSS, ставим знак «/», щелкаем мышью по ячейке, содержащей значение суммы TSS, закрываем скобку, нажимаем Enter.
7. Находим коэффициент детерминации по третьей формуле:
R2 = r(y, yэмп )2 ,
где
r(y, yэмп )2 =cov(y, yэмп) / (var(y)*var(yэмп)) ,
cov(y, yэмп)= 1/( t-1)* Σ (y- 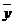 )* (yэмп-
)* (yэмп- 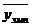 ).
).
Для этого выполняем промежуточные действия:
а) находим 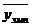 аналогично
аналогично 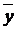 из первого задания;
из первого задания;
b) находим сумму из формулы ковариации: выделяем ячейку, в выделенной ячейке ставим знак «=», открываем скобку, щелкаем мышью по ячейке, содержащей первое значение y, ставим знак «-», далее щелкаем мышью по ячейке, содержащей значение 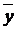 , фиксируем его в верхней строке формулы знаком «$» перед буквой и перед цифрой, закрываем скобку, ставим знак «*», открываем скобку, щелкаем мышью по ячейке, содержащей первое значение yэмп, ставим знак «-», далее щелкаем мышью по ячейке, содержащей значение yэмп и фиксируем его в верхней строке формулы знаком «$» перед буквой и перед цифрой, закрываем скобку, нажимаем Enter. Удерживая левую кнопку мыши, протягиваем вниз еще на 14 ячеек. Находим сумму получившихся значений: щелкаем по ячейке, находящейся ниже этих значений, ставим знак «=», выбираем значок ∑ (автосумма) на панели инструментов и выделяем с помощью мыши все получившиеся значения произведений, нажимаем Enter;
, фиксируем его в верхней строке формулы знаком «$» перед буквой и перед цифрой, закрываем скобку, ставим знак «*», открываем скобку, щелкаем мышью по ячейке, содержащей первое значение yэмп, ставим знак «-», далее щелкаем мышью по ячейке, содержащей значение yэмп и фиксируем его в верхней строке формулы знаком «$» перед буквой и перед цифрой, закрываем скобку, нажимаем Enter. Удерживая левую кнопку мыши, протягиваем вниз еще на 14 ячеек. Находим сумму получившихся значений: щелкаем по ячейке, находящейся ниже этих значений, ставим знак «=», выбираем значок ∑ (автосумма) на панели инструментов и выделяем с помощью мыши все получившиеся значения произведений, нажимаем Enter;
с) находим ковариацию. Выделяем ячейку, ставим знак «=», нажимаем 1, ставим знак «/» на клавиатуре набираем 14 (так как t =15, в формуле t-1), щелкаем мышью по ячейке, содержащей значение суммы из пункта b, нажимаем Enter;
d) находим var-дисперсию y и yэмп. Выделяем ячейку, ставим знак «=», выбираем значок fx на панели инструментов, затем находим ДИСП в окне меню, нажимаем OK, выделяем область по y, которая заносится в поле Число 1. Нажимаем OK. Аналогично находим дисперсию для величины yэмп ;
e) находим произведение дисперсий. Выделяем ячейку, ставим знак «=», щелкаем мышью по ячейке, содержащей значение дисперсии y, ставим знак «*», далее щелкаем мышью по ячейке, содержащей значение дисперсии yэмп , нажимаем Enter;
f) извлекаем корень из произведения дисперсий. Выделяем ячейку, ставим знак «=», выбираем значок fxна панели инструментов, затем находим КОРЕНЬ в окне меню, нажимаем OK, выделяем ячейку со значением из пункта e, которая заносится в поле. Нажимаем OK;
g) находим коэффициент корреляции r. Выделяем ячейку, ставим знак «=», щелкаем мышью по ячейке, содержащей значение ковариации из пункта с, ставим знак «/», далее щелкаем мышью по ячейке, содержащей значение корня из пункта f , нажимаем Enter;
h) находим коэффициент детерминации по третьей формуле. Выделяем ячейку, ставим знак «=», щелкаем мышью по ячейке, содержащей значение коэффициента корреляции r из пункта g, ставим знак «*» и щелкаем по той же ячейке, нажимаем Enter.
8. Проверяем адекватность модели с помощью F-теста. Вычисляем значение F-критерия на основе формулы:
F = R2/((1- R2)/(t-2)),
где t =15 - число наблюдений.
Выделяем ячейку, ставим знак «=», щелкаем мышью по ячейке, содержащей значение коэффициента детерминации R2 из пункта 6, ставим знак «/», ставим скобки (( , затем 1, ставим знак «-», и щелкаем по той же ячейке R2, первую скобку закрываем, ставим знак «/», число 13, вторую скобку закрываем, нажимаем Enter.
9. Находим F табличное для уровней значимости 0,05 и 0,01.
Если F, полученное в пункте 8, больше F табличного для данного уровня значимости, то нулевая гипотеза H0 отклоняется на этом уровне значимости.
11. Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации:
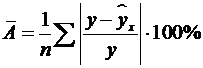
Средняя ошибка аппроксимации не должна превышать 8–10%.
Варианты для парной регрессионной модели
Вариант № 1
 | ||||||||||
 | ||||||||||
 |
Вариант № 2
 | ||||||||||
 | ||||||||||
 |
Вариант № 3
 | ||||||||||
 | ||||||||||
 |
Вариант № 4
 | ||||||||||
 | ||||||||||
 |
Вариант № 5
 | ||||||||||
 | ||||||||||
 |
Вариант № 6
 | ||||||||||
 | ||||||||||
 |
Вариант № 7
 | ||||||||||
 | ||||||||||
 |
Вариант № 8
 | ||||||||||
 | ||||||||||
 |
Вариант № 9
 | ||||||||||
 | ||||||||||
 |
Вариант № 10
 | ||||||||||
 | ||||||||||
 |
Вариант № 11
 | ||||||||||
 | ||||||||||
 |
Вариант № 12
 | ||||||||||
 | ||||||||||
 |
Вариант № 13
 | ||||||||||
 | ||||||||||
 |
Вариант № 14
 | ||||||||||
 | ||||||||||
 |
Вариант № 15
 | ||||||||||
 | ||||||||||
 |
Вариант № 16
 | ||||||||||
 | ||||||||||
 |
Вариант № 17
 | ||||||||||
 | ||||||||||
 |
Вариант № 18
 | ||||||||||
 | ||||||||||
 |
Вариант № 19
 | ||||||||||
 | ||||||||||
 |
Вариант № 20
 | ||||||||||
 | ||||||||||
 |
Вариант № 21
 | ||||||||||
 | ||||||||||
 |
Вариант № 22
 | ||||||||||
 | ||||||||||
 |
Вариант № 23
 | ||||||||||
 | ||||||||||
 |
Вариант № 24
 | ||||||||||
 | ||||||||||
 |
Вариант № 25
 | ||||||||||
 | ||||||||||
 |
Вариант № 26
 | ||||||||||
 | ||||||||||
 |
Вариант № 27
 | ||||||||||
 | ||||||||||
 |
Вариант № 28
 | ||||||||||
 | ||||||||||
 |
Вариант № 29
 | ||||||||||
 | ||||||||||
 |
Вариант № 30
 | ||||||||||
 | ||||||||||
 |
Лабораторная работа №5
Множественная регрессионная модель.
Классическая линейная модель
Классическая (нормальная) модель линейной множественной регрессии (КЛММР) имеет вид:
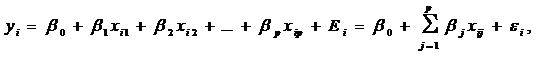 (1)
(1)
где  - значение результирующей переменной;
- значение результирующей переменной; 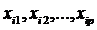 - значение 1-го, 2-го,…, р-го регрессора в i-ом наблюдении (i = 1,2,…,n); β0, β1, βp - числовые коэффициенты; εi - случайные (стохастические) составляющие или ошибки (возмущения).
- значение 1-го, 2-го,…, р-го регрессора в i-ом наблюдении (i = 1,2,…,n); β0, β1, βp - числовые коэффициенты; εi - случайные (стохастические) составляющие или ошибки (возмущения).
Переписывая выражение (1) в виде системы уравнений для различных значений (i = 1,2,…,n), их можно представить в матричном виде:
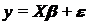 , (2)
, (2)
где 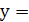
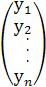 - вектор объясняемых переменных;
- вектор объясняемых переменных;
ε= 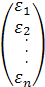 - вектор значений ошибки;
- вектор значений ошибки; 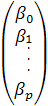 - вектор коэффициентов;
- вектор коэффициентов;
X= 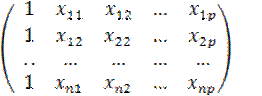 - матрица объясняющих переменных размером n×(p+1), в которой первый столбец с единичными элементами соответствует в выражении (1) умножению
- матрица объясняющих переменных размером n×(p+1), в которой первый столбец с единичными элементами соответствует в выражении (1) умножению 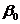 на единицу.
на единицу.
Основные предпосылки (гипотезы) КЛММР:
1. Х – детерминированная матрица.
2. Математическое ожидание возмущения ε0 равно нулю:
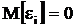 ( i = 1,2,…,n),
( i = 1,2,…,n),
где М[·] знак математического ожидания.
3. Дисперсия возмущения постоянна для любых значений i (условие гомоскедастичности):
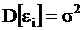 ( i = 1,2,…,n),
( i = 1,2,…,n),
где D[·] знак дисперсии;
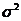 - величина дисперсии.
- величина дисперсии.
4. Возмущения для разных наблюдений являются некоррелированными:
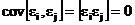 при
при 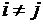 ,
,
где 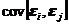 - коэффициент ковариации.
- коэффициент ковариации.
Условия 3 и 4 можно объединить в одно, определяющее вид ковариационной матрицы возмущений:
Cε = 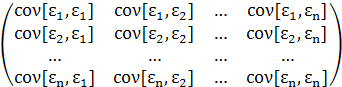 =
=
= 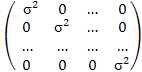 =
= 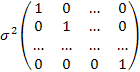 =
= 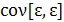 =M[ε
=M[ε 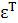 ]=
]= 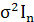 ,
,
где 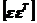 - векторное произведение вект
- векторное произведение вект
