Определение марковских процессов и цепей Маркова
Введем, прежде всего, понятие случайного процесса в целом: случайным (или стохастическим) процессом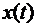 
называется функция времени t, значения которой представляют собой случайные переменные. Если каждая случайная переменная может принимать при этом лишь конечное или счетное множество значений, мы имеем процесс с дискретными состояниями или цепь. В противном случае имеем процесс с непрерывными состояниями.
Для идентификации состояний цепи 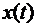можно использовать натуральные числа. Так, если 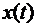находится в состоянии j в момент времени t, мы говорим, что 
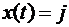, где j – натуральное число.
Далее, если моменты времени, в которые возможны переходы от одного случайного события к другому (то есть смена состояний системы), образуют конечное или счетное множество, мы имеем процесс с дискретным временем или стохастическую (случайную) последовательность. Эти моменты времени можно заменить целыми значениями индекса времени i, и, значит, стохастическую последовательность можно обозначить как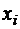 
, 
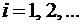Конечная стохастическая последовательность называется временным рядом. Если же такие переходы могут происходить в любой точке непрерывной оси времени, то процесс относится к процессам с непрерывным временем (рис. 1).
С точки зрения математики случайный процесс нужно описывать условной вероятностью
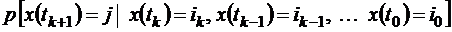
находиться в состоянии j в момент времени tk+1.
 |
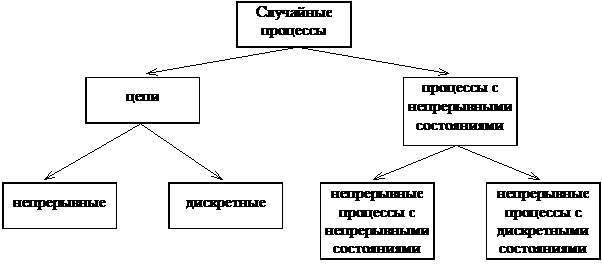Рис. 1
Простейшими из всех типов случайных процессов являются процессы с независимыми значениями. Случайный процесс называется процессом с независимыми значениями, если для любого (k+1)-го события (истинность которого в принципе должна зависеть от исходов всех предшествовавших ему событий до k-го)
.
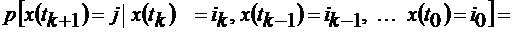
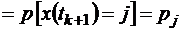Для таких процессов знание исходов всех уже наблюдавшихся (совершившихся) событий не влияет на наш прогноз относительно исхода последующего события. Например, это относится к процессу подбрасывания монеты – «орел» или «решка». Для марковских же процессов нужно ослабить это требование, допустив, что знание исхода непосредственно предшествовавшего события (но только его одного!) может влиять на этот прогноз.
Марковский процесс – это случайный процесс 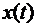, для которого вероятность того, что в момент времени tk+1 процесс находится в состоянии j, зависит только от его состояния в момент времени tk для любой последовательности моментов времени 
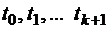, такой, что 
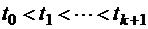, то есть
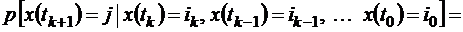
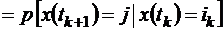
или просто
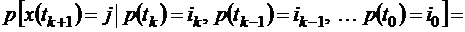
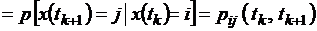. (1.1.1)
Зависимость (1.1.1) называется марковским свойством и определяет класс так называемых марковских процессов. Ввиду большой важности этих процессов для дальнейшего изложения дадим еще одно их определение, отличающееся особенной простотой и наглядностью с точки зрения возможных приложений.
Случайный процесс называется марковским, если для любого момента времени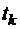 
вероятность каждого из состояний системы в будущем (при 
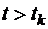) зависит только от состояния системы в настоящем (при 
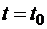) и не зависит от того, когда и как она пришла в это состояние, то есть не зависит от поведения этой системы в прошлом (при 
).
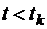Вообще говоря, каждая цепь Маркова эквивалентна некоторой схеме с урнами в следующем смысле. Допустим, что имеется ряд урн, каждая из которых обозначена меткой 1, 2, 3рядаи так далее. В урнах находятся шары, также пронумерованные при помощи натуральных чисел. Состав урн остается неизменным (во времени), но меняется от урны к урне так, что вероятность извлечь шар с k-й меткой из j-й урны равна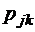 
. Начальное (нулевое) событие состоит в том, что в соответствии с некоторым заданным начальным распределением вероятностей 
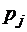среди этих урн выбирается случайным образом какая-либо одна урна с индексом j. Из этой урны также случайным образом извлекают шар и, если его метка k, то следующий шар извлекают уже из k-й урны, и так далее. Как видим, в этом случае исход любого события зависит от исхода предыдущего события (и только от него одного). Процессы с независимыми значениями (независимые события) являются при этом, очевидно, лишь частным случаем указанной выше схемы. В этом случае 
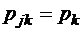для любого j.
Следует также отметить, что случайный процесс, у которого условные вероятности состояний в будущем зависят только от состояния на данном (последнем) шаге и не зависят от предыдущих состояний, иногда называют простым марковским процессом. Процессы, у которых будущее зависит от состояний системы не только на данном шаге (то есть в настоящем), но и от ее состояний на нескольких предыдущих шагах, принято называть сложными марковскими процессами.
При исследовании СМО аналитическими методами (то есть при их аналитическом моделировании) наибольшее значение имеют марковские случайные процессы с дискретными состояниями и непрерывным временем или, как их обычно называют, непрерывные марковские цепи, к изучению которых мы переходим.