Линейные автоматические системы

1. Получение уравнений элементов систем автоматического регулирования.

Упражнение 1.Уравнение емкости с газом. Емкость будем рассматривать как объект, в котором требуется регулировать давление газа.

Обозначим символами Р _г , Т _г и V_г соответственно давление, температуру и объем газа в емкости. Массовые расходы газа в емкость и из емкости обозначим соответственно символами G _П и G _B.

Исходным уравнением, отражающим термодинамическое равновесное состояние газа в емкости, служит уравнение состояния

. (1.1)

Дополняющими уравнениями являются зависимости, определяющие расходные характеристики :

и ,

где параметр 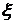определяет режим работы компрессора, подающего газ в емкость, а параметр регулирует количество газа, выходящего из емкости.

Можно упростить задачу, считая, что для небольших давлений в емкости температура газа в процессе наполнения не изменяется (T_г = сonst) и также не изменяется режим работы компрессора ( = сonst). В этом варианте можно записать:

и . (1.2)

Расходные характеристики часто задают с помощью экспериментально полученных кривых. В данном случае эти характеристики нелинейные, рис.1.2.

Для составления уравнения емкости запишем уравнение состояния в виде

= .

Далее можно записать . Представленное выражение также соответствует записи . Приравнивая правые части последних двух равенств, получим искомое уравнение

(1.3)

Так как зависимости G_B и G_П нелинейные (рис.1.2), то и уравнение (1.3) нелинейное.

Для получения стандартных описаний нелинейные уравнения должны быть линеаризованы, если это возможно. Предположим, что исходная предпосылка о малости отклонений переменных от установившихся значений выполняется. В этом случае возможна линеаризация с помощью разложения в ряд Тейлора нелинейного описания (1.3).

Видно, что в уравнении (1.3) две переменные: и . Так как емкость рассматривается как объект управления, то можно утверждать, что давление газа в емкости является регулируемой величиной, а перемещение заслонки - регулирующим воздействием, рис.1.3.

Нелинейными функциями являются расходы газа и , рис.1.2. Для линеаризации уравнение (1.3) запишем в неявном виде

(1.4)

Уравнение (1.4) разложим в ряд Тейлора

, (1.5)

где - значение функции (1.4) на установившемся режиме; , , .

Вычтем из выражения (1.5) составляющую . В результате получим искомое линеаризованное уравнение .

. (1.6)

Далее это уравнение необходимо записать в стандартной форме.

Регулируемой величиной в линеаризованном уравнении будет переменная . Регулирующей величиной – переменная . Символ обозначает отклонение переменных и от их значений в установившемся режиме. Для упрощения в последующих записях символ применяться не будет. При этом переменные и будут обозначать не сами величины, а их отклонения.

Введем в рассмотрение оператор дифференцирования и, учитывая замечания относительно обозначения переменных, запишем уравнение (1.6) в виде

. (1.7)

Далее, выполним очевидные преобразования:

. (1.8)

В результате получена первая форма записи уравнения. Осталось лишь применить обозначения в виде постоянной времени , равной дроби в левой части уравнения и коэффициента передачи , равному дроби в правой части уравнения. С учетом обозначений уравнение (1.8) примет вид

. (1.9)

Переменные уравнения и имеют свои размерности, соответственно и . Однако, в практике исследований применяются также и уравнения с безразмерными переменными.

Приведем уравнение (1.9) к безразмерному виду. Для этого уравнение удобно записать с применением обозначений :

.

Разделим левую и правую части уравнения на (давление газа на установившемся режиме), а правую часть разделим и умножим на (положение заслонки на установившемся режиме). В результате получим

.

Или

где , а = и = безразмерные отклонения переменных.

Упражнение 2.Уравнение гидравлической емкости. В рабочей емкости (рис.1.4) должен поддерживаться постоянный уровень жидкости 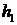. Примером такой емкости может служить плюсовка машины для непрерывного крашения тканей. В плюсовке должен поддерживаться постоянный уровень красильного раствора , что необходимо для стабильной пропитки ткани красильным раствором и равномерной окраски ткани.

Унос красильного раствора из плюсовки обусловлен движущейся тканью с различной влажностью на входе в рабочую емкость 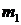и на выходе из нее 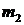. Массовый расход ткани 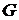. Унос раствора тканью компенсируется подачей подкрепляющего раствора 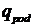через клапан с проходным сечением 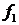. Клапан играет роль регулирующего органа. Регулируемая величина – уровень жидкости в емкости, регулирующее воздействие – изменение проходного сечения клапана 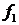. Возмущающие воздействия – изменения .

Основными уравнениями, описывающими процесс изменения уровня жидкости в рабочей емкости, являются:

1.Уравнение баланса жидкости

, (1.10)

где приращение объема жидкости в емкости за время ;

объемный секундный расход жидкости в емкость;

объемный секундный расход жидкости из емкости.

Рис. 1.4. Гидравлическая емкость

При вертикальных стенках рабочей емкости

, (1.11)

где площадь «зеркала» жидкости, приращение уровня жидкости за время .

Подставляя (1.11) в (1.10) и, переходя к бесконечно малым приращениям и , уравнение баланса жидкости запишем в виде

. (1.12)

2. Уравнение расхода жидкости через клапан с проходным сечением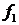

, (1.13)

где коэффициент расхода, учитывает влияние местных сопротивлений;

ускорение силы тяжести.

3.Уравнение уноса жидкости тканью из рабочей емкости

, (1.14)

где - плотность жидкости.

Подставляя (1.13) и (1.14) в уравнение баланса (1.12), получим уравнение гидравлической емкости как объекта управления

. (1.15) Видно, что уравнение нелинейное. В уравнении переменная 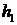является регулируемой величиной, переменная 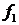регулирующим воздействием. Изменения переменных являются возмущающими воздействиями. Для упрощения примем, что эти воздействия отсутствуют. С учетом этого допущения выполним линеаризацию уравнения (1.15).

Уравнение (1.15) запишем в неявном виде

. (1.16)

Далее разложим уравнение (1.16) в ряд Тейлора \ 1 \. В результате получим

, (1.17)

где значение функции (1.16) на установившемся режиме;

(1.18)

В выражении (1.17) отбросим члены высшего порядка малости и вычтем из него постоянную величину и запишем его с учетом выражений для частных производных (1.18). В результате получим

.

Разделим на коэффициент при и перенесем за знак равенства член уравнения с отклонением . В результате получим

.

Далее применим, оператор дифференцирования и обозначения коэффициентов и 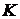при переменных и соответственно. В результате получим искомое линеаризованное уравнение

.

Упражнение 3.Уравнения корректирующих электрических цепей. В электронике широко применяются корректирующие пассивные RC цепи. При этом может достигаться эффект фильтрации сигналов в диапазонах низких и высоких частот.

Уравнение фильтра сигналов низкой частоты. Электрическая схема RC цепи представлена на рис.1.5,а. Запишем уравнение баланса напряжений для цепи RC где напряжение .

Дифференцируя, последовательно получим , . Подставив полученное выражение в уравнение баланса напряжений, получим искомое уравнение

.

Или, в стандартном виде: , где - постоянная времени и оператор дифференцирования.

Для оценки свойств фильтра построим логарифмическую амплитудно-частотную характеристику . Выражение для частотной передаточной функции имеет вид . Соответствующая ей формула для амплитудно-частотной характеристики . Сопрягающая частота . Далее записываем уравнения асимптот :

если , то и ;

если , то и .

На рис.1.5,а также изображена и логарифмическая характеристика. Видно, что для частот меньших сопрягающей частоты, корректирующее устройство является фильтром, так как на этих частотах амплитуда выходного сигнала равна единице. Для частот превышающих сопрягающую частоту имеет место усиление выходного сигнала с интенсивностью 20 дб за дек.

Уравнение фильтра сигналов высокой частоты. Схема RC цепи представлена на рис.1.5,б. Запишем уравнение баланса напряжений . Выполним замену и продифференцируем уравнение напряжений. В результате получим искомое уравнение

.

Или в стандартном виде

, где .

Запишем выражение для АЧХ . Потребуем, чтобы произведение Т= RC было меньше единицы. Пусть, например, Тогда сопрягающая частота

Если , то и . Если , то и .

На рис.1.5,б изображена логарифмическая характеристика корректирующего устройства. Видно, что в данном случае фильтруются высокочастотные сигналы.

Упражнение 4. Уравнение тахогенератора. Тахогенератор (маломощный генератор) постоянного тока с возбуждением от постоянных магнитов, рис.1.6.

Рис.1.6. Электрическая схема тахогенератора

Для получения уравнения тахогенератора необходимо применить уравнение баланса напряжений в цепи якоря

. (1.19)

В соответствие с уравнением электродвижущая сила , вырабатываемая генератором, расходуется на падение напряжений на активном ( ) и индуктивном сопротивлениях цепи якоря генератора.

Напряжение на зажимах генератора и ток якоря .

Дифференцируя левую и правую части второго уравнения, можно записать

(1.20)

С учетом (1.20) уравнение (1.19) можно записать в виде

где с – постоянный коэффициент, зависит от конструкции ротора;

Ф – плотность магнитного потока возбуждения;

– угловая скорость вращения ротора двигателя.

Вводя, оператор дифференцирования , получим

(1.21)

где .

Так как угловая скорость , где - угол поворота ротора генератора, то уравнение (1.21) можно записать в окончательном виде

. (1.22)

Уравнение (1.22) применяется в случае, когда тахогенератор используется в качестве корректирующего элемента. В этом случае тахогенератор является дифференцирующим звеном. Уравнение (1.21) относится к апериодическому звену и применяется, когда тахогенератор используется в качестве датчика скорости вращения ротора.

Упражнение 5. Уравнение двигателя постоянного тока независимого возбуждения. Применяется в качестве исполнительного элемента в системах автоматического регулирования.

Рис.1.7. Электрическая схема и механическая характеристика двигателя ( пусковой момент, угловая скорость на холостом режиме, напряжение, соответствующее холостому режиму ).

На рис.1.7,а изображена схема якорной цепи двигателя. Определим передаточную функцию двигателя. Для этого запишем уравнения двигателя.

Уравнение баланса напряжений

, (1.23)

где – напряжение, приложенное к цепи якоря двигателя;

- ток в цепи якоря; - напряжение обратной э.д.с;

- индуктивность цепи якоря;

конструктивный коэффициент, , рис.1.7,б;

- активное сопротивление цепи якоря.

Дифференциальное уравнение движения якоря двигателя , , (1.24)

где - вращающий момент двигателя;

коэффициент момента двигателя (в системе СИ коэффициенты и по величине равны друг другу;

момент инерции нагрузки;

- статический момент нагрузки.

Далее необходимо перейти к операторной форме записи и совместно решить уравнения (1.23) и (1.24). Если принять , то уравнение двигателя при этом получается следующим

, (1.25)

где коэффициент передачи двигателя; - электромеханическая постоянная времени; электромагнитная постоянная времени.

Величина постоянной времени для двигателей постоянного тока с независимым возбуждением находится в пределах 0.04 – 0.2 с. Величина постоянной времени в несколько раз меньше. В случаях, когда уравнение (1.25) можно применять в виде

(1.26)

Выражение (1.25), как и выражение (1.26) являются описаниями интегрирующего звена. Отличаются они лишь тем, что в первом случае - интегрирующее звено второго порядка, а во втором случае – с интегрирующее звено первого порядка. Если за выходную величину принять не угол поворота вала двигателя , а угловую скорость , то уравнения (1.25) и (1.26) преобразуются в уравнения апериодических звеньев первого и второго порядков:

; ..

Упражнение 6. Уравнение пассивной электрической цепи.Схема цепи представлена на рис.1.8,а. Получим передаточную функцию и дифференциальное уравнение относительно напряжений и . Для получения описания передаточной функции удобно пользоваться операторной формой записи сопротивлений: индуктивного - емкостного - и активного – R, где оператор дифференцирования.

Преобразуем электрическую цепь на рис.1.8,а в эквивалентную ей цепь на рис.1.8,б, где

(1.27)

Так как падение напряжения на последовательно соединенных сопротивлениях пропорционально величине сопротивлений, то передаточная функция эквивалентной цепочки (рис.1.8,б) находится как отношение

(1.28)

Подставляя выражения (1.27) в формулу (1.28), получим передаточную функцию электрической цепи

и искомое уравнение

где

2. Получение уравнений систем автоматического регулирования

Упражнение 7. Применение метода структурных преобразований. На рис.2.1,а изображена структурная схема некоторой САР с дополнительной обратной связью. Передаточные функции элементов системы имеют вид:

Требуется получить уравнение движения

Для получения уравнения необходимо исходную схему последовательно преобразовывать в структуры, изображенные на рис.2.1,б, в, г.

При этом получаемые промежуточные передаточные функции имеют вид:

;

;

.

Далее, подставив выражения для передаточных функций, получим передаточную функцию системы по управляющему воздействию

,

где коэффициент передачи разомкнутой системы.

Полученная передаточная функция позволяет записать уравнения системы

,

где:

Из содержания уравнения следует, что для данной системы

и .

Задача 1.Для рассматриваемой в упражнении 7 системы получить уравнение ошибки.

Ответ:

Задача 2.Получить уравнение следящей системы для обработки деталей по контуру.На рис.2.2 изображена схема устройства следящей системы.

В состав схемы вошли следующие элементы:

1 - следящее пневматическое сопло;

2 обрабатываемая деталь;

3 - рабочий орган (игла);

4 - пневматический датчик с сильфоном;

5 - управляющее устройство (золотник);

6 – шток золотника;

7 - гидравлический двигатель:

8 - преобразователь движения;

9 - рычаг жесткой обратной связи;

10 - подвижный стол.

Работа системы состоит в следующем. Основу пневматического датчика составляет подпружиненный изнутри сильфон. На вход датчика подается сжатый воздух - управляющее давление . Сжатый воздух может покидать полость датчика через пневматическое сопло 1. Сопло 1 прикрепляется к рабочему органу таким образом, чтобы край обрабатываемой детали находился в определенном месте сопла (рис.2.3, а). При этом в полости датчика (рис.2.2) установится давления , при котором сила давления на поверхность сильфона будет равна его упругой силе. Вследствие равенства сил, шток золотника останется в нейтральном положении, поршень двигателя также будет неподвижен.

\

Рис.2.3. Упрощенная схема крепления сопла

Сила, действующая на сильфон слева направо, будет равна , где эффективная площадь сильфона. Величина противодействующей ей упругой силы сильфона устанавливается при монтаже системы. На рис.2.3,б показана упрощенная схема сопла с заслонкой.

Структурная схема следящей системы представлена на рис.2.4. При составлении схемы приняты следующие обозначения:

ПД – пневматический датчик; ГД – гидравлический двигатель;

ЖОС – жесткая обратная связь; Пр - преобразователь движения;

Ст - подвижный стол; С с - следящее сопло.

Передаточные функции элементов следящей системы:

гидравлический двигатель ;

пневматический датчик ;

жесткая обратная связь ;

преобразователь движения ;

следящее сопло .

Ответ: Уравнение системы , где

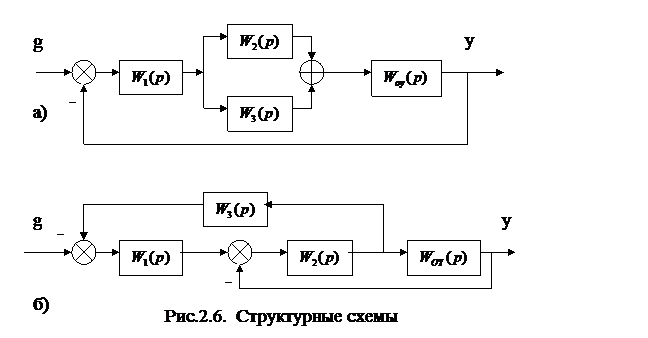
Задача 3. Получить дифференциальное уравнение движения для систем, представленных структурными схемами на рис. 2.6.

Передаточные функции имеют вид:

.

Ответ: ,

где:

Упражнение 8.Уравнения состояния. Уравнение системы или объекта управления может быть представлено в виде системы дифференциальных уравнений первого порядка в так называемой форме Коши. Пусть уравнение объекта имеет вид

(2.1)

где ; , .

Введем независимых переменных , называемых переменными состояния, и представим уравнение в виде системы дифференциальных уравнений

(2.2)

Эти уравнения, как и уравнение (2.1), полностью характеризуют состояние объекта в любой момент времени и поэтому называются уравнениями состояния. Связь между переменными уравнений состояния и управляемой величиной устанавливается алгебраическим уравнением

. (2.3)

В выборе переменных состояния имеется определенная свобода. Важно, чтобы они были независимыми. Однако целесообразно в качестве переменных состояния использовать саму управляемую величину и ее производные:

(2.4)

Иногда уравнения (2.1) и (2.2) записывают в векторно-матричной форме:

(2.5)

где матрица коэффициентов уравнений состояния размером , матрицы - столбцы.

В общем случае матрица имеет вид

(2.6)

Форму можно использовать лишь в случае отсутствия в правой части уравнения (2.1) производных от и .

В качестве переменных состояния можно также использовать промежуточные координаты / 2 / , представляющие собой некоторые составляющие переходного процесса. Получаемая при этом система уравнений первой степени называется замещающей. Пусть переходный процесс соответствует следующему уравнению

Замещающая система уравнений имеют вид

Из содержания записи следует, что последняя составляющая является переменной . В этом можно убедиться, свернув замещающую систему уравнений, посредством исключения промежуточных переменных .

Упражнение 9. Записать уравнения состояния и матрицы коэффициентов для уравнения

(2.7)

Решение. Уравнение (2.7) запишем относительно старшей производной

Назначим переменные состояния:

(2.8)

Запишем уравнения состояния

Матрицы коэффициентов получаются следующими

Из (2.8) следует, что . Поэтому в уравнении (2.3)

.Упражнение 10. Записать уравнения состояния и матрицы коэффициентов для системы третьего порядка

, (2.9)

Решение. В общем виде уравнения состояния будут иметь вид

В качестве переменных состояния выбирается сама управляемая величина и ее производные

Из уравнения (2.9) найдем выражение относительно старшей производной

(2.10)

С учетом принятых переменных и выражения (2.10) уравнения состояния примут следующий вид

(2.11)

где матрицы коэффициентов в случае векторной записи исходных уравнений оказываются следующими

= =

Задача 4.Записать замещающую систему уравнений

.

Задача 5. Получить исходное уравнение, по виду замещающей системы уравнений

Задача 6. Определить характеристический полином системы, у - регулируемая величина

Задача 7.Записать уравнение ошибки, для системы управления, описываемой следующими уравнениями:

( - управляющее воздействие, - регулируемаяпеременная).