Проверяем правильность вычисления опорных реакций (сумма проекций всех сил на вертикальную ось z должна быть равна 0)

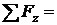+ R_A – q·3 + R_B – F = 11,5– 15·3 + 63,5 – 30 =75 – 75=0.

б) определение внутренних усилий

Расчетная схема балки имеет три участка (рис.17).

I участок (сечение перемещается от левой до правой границы).

Составляем выражение для поперечной силы с учетом правила знаков (см. рис.13) слева от сечения (рис.17)

Q(x₁) = R_A =11,5 кН(прямая линия параллельная оси x).

Составляем выражение для изгибающего момента с учетом правила знаков слева от сечения

M(x₁)=R_A x₁ = 11,5 x₁(уравнение прямой линии);

M(0)=0(значение на левой границе участка);

M(2)= 11,5·2=23 кНм(значение на правой границе участка).

Рис.17

II участок (сечение перемещается от левой до правой границы).

Составляем выражение для поперечной силы с учетом правила знаков слева от сечения (рис.17)

Q(x₂)= R_A– q( x₂- 2) = 11,5- 15( x₂- 2)=41,5- 15 x₂ (уравнение прямой линии).

Здесь q(x₂ -2) - равнодействующая сила распределенной нагрузки q, располо- женная слева от сечения посредине участка длиной (x₂ -2);

Q(2)= 41,5- 30=11,5 кН(значение на левой границе участка);

Q(5)= 41,5 -15·5=41,5 -75 = -33,5 кН(значение на правой границе участка).

Поскольку поперечная сила меняет знак в пределах участка, определяем координату, при которой она обращается в нуль (в этом сечении изгибающий момент принимает экстремальное значение):

Q(x₀) = 41, 5- 15x₀=0; x₀=41, 5/15=2, 77 м.

Составляем выражение для изгибающего момента с учетом правила знаков слева от сечения

M(x₂) =

(уравнение квадратичной параболы);

M(2)= 3 кНм (значение на левой границе участка);

M(2,77)= 7,408 кНм=7,41 кНм;

M(5)= – 30 кНм (значение на правой границе участка).

Рис.18

III участок (сечение перемещается от правой до левой границы).

Составляем выражение для поперечной силы с учетом правила знаков справа от сечения (см. рис.17), т.к. справа меньше сил.

Q(x₃)= F = 30 кН(прямая линия параллельная оси x).

Составляем выражение для изгибающего момента с учетом правила знаков справа от сечения

M(x₃)= – F x₃ = - 30x₃ (уравнение прямой линии);

M(0)= 0 кНм (значение на правой границе участка);

M(1)= - 30 кНм (значение на левой границе участка).

Используя полученные значения, строим в масштабе эпюры поперечных сил и изгибающих моментов, как показано на рис.18.

Определение опасного сечения по нормальным напряжениям

В опасном сечении M_max =30 кНм = 30×10^-3 МНм (сечение B на рис.18).

Подбор сечения балки из прокатного профиля по методу

Допускаемых напряжений

Из условия прочности (2) определяем требуемую величину момента сопротивления

.

По сортаменту прокатной стали для двутаврового сечения ближайшим к является значение момента сопротивления =184 см³ (двутавр №20).

Проверка прочности балки

Для двутавра №20 184см³=184·10^{-6 м3};

проверяем выполнение условия прочности:

163,049 МПа=163 МПа> [s ] =160 МПа.

На основании полученного результата устанавливаем, что балка перегружена. Определяем величину перегрузки

×100 % %=1,88 % <5%.

Условие 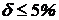выполняется, поэтому окончательно выбираем двутавр №20.

Задача 4

Чугунный короткий стержень, поперечное сечение которого изображено на рис.19, сжимается продольной силой F, приложенной в точке К. Требуется:

1.Вычислить величины роверить прочность балок. наибольших растягивающих и сжимающих напряжений в

поперечном сечении, выразив величины этих напряжений через F.

2. Из условий прочности найти допускаемую нагрузку [F] при заданных

значениях допускаемых нормальных напряжений для чугуна на сжатие [ s_с] и

на растяжение [ s_р].

Исходные данные:

a=4 см; b=6 см;

[ s_с] = 160МПа=160 ;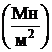

[ s_р] = 40МПа=40 .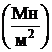

Рис.19

Решение

Будем считать, что пластина - фигура I, а полукруг -фигура II. Используя справочные таблицы, выписываем данные для каждой фигуры.

Фигура I- прямоугольник 4см´6 см

b=4см;h=6 см; A₁= b h= 4∙6см²=24 см²;

Фигура II - полукруг, диаметра d=2b=12см

z₀=0, 212d =0, 212∙12см=2, 544=2, 54см;

.

Нормальные напряжения в случае внецентренного сжатия находятся по формуле:

. (5)

В этой формуле:s - величина нормального напряжения в любой точке сечения c координатами y, z;

F- величина внецентренной силы, приложенной в точке K; A - площадь поперечного сечения;

y_K, z_K - координаты точки приложения силы, взятые относительно главных

центральных осей заданного сечения;

, - квадраты радиусов инерции, которые определяются по формулам:

, .

Используя приведенные выше справочные данные, вычерчиваем сечение в масштабе с указанием всех осей и необходимых размеров в сантиметрах (рис.20). На рис.20 в рамках показаны размеры, взятые из справочных данных, остальные получены в ходе расчета.