Замечание. В строительных организациях эпюра изгибающих моментов строит-

ся на растянутом волокне, поэтому на эпюре M вместе со знаком

Пунктиром показаны положения растянутых волокон.

Рис.14

Замечание. Длину балки, а также эпюры поперечных сил и изгибающих

Моментов необходимо вычертить в масштабе. Приведем один из

возможных вариантов: масштаб длины балки 1 см : 0,5м;

масштаб оси Q - 1 см : 10 кН; масштаб оси M - 1 см : 5 кНм.

Определение опасного сечения по нормальным напряжениям

Определение. Сечение, в котором изгибающий момент принимает наибольшее по абсо-

лютной величине значение, называют опасным сечением балки по нормаль-

ным напряжениям.

В опасном сечении M_max=11,3 кНм = 11,3×10^-3 МНм (сечение B на рис.14).

Подбор сечения балки по методу допускаемых напряжений при изгибе

Условие прочности при изгибе по нормальным напряжениям по методу допускаемых напряжений имеет вид:

s_max [s]. (2)

В этой формуле:s_max - максимальное нормальное напряжение;

M_max - наибольшее по абсолютной величине значение изгибающего момента (определяется по эпюре изгибающих моментов);

- момент сопротивления относительно оси y(горизонтальная ось);

[s ] - допускаемое нормальное напряжение.

Момент сопротивления относительно оси y

, (3)

где – момент инерции относительно оси y; – максимальное расстояние, измеряемое по оси z от центра тяжести до крайних точек поперечного сечения.

Применяя условие прочности, можно выполнить три вида расчета:

1.Проектный расчет. По заданной нагрузке определяют наибольший изгибающий момент M_max и из условия прочности находят величину требуемого момента сопротивления по формуле: . (4)

Размеры сечения подбирают из условия: , где момент сопротивления определяется через размеры поперечного сечения по формуле (3) или по спра-вочным таблицам для прокатных профилей.

2.Определение допускаемой нагрузки. По известному моменту сопротивления и допускаемому напряжению находят наибольшую величину изгибающего момента

M .

3.Проверочный расчет. По известным значениям M_max, W_y, [s] проверяют

выполнение условия прочности (2).

Используя неравенство (4), определяем требуемую величину момента сопротивления .

Момент сопротивления круглого сечения диаметра d (см. справочные таблицы) .

Приравнивая и , получаем ³ 11, 3×10^{-4 м3}.

Откуда находим диаметр d

d ³ 0,22582 м = 0, 226 м = 22, 6 см.

Принимаем диаметр d =22, 6 см.

Проверка прочности балки

Проверяем выполнение условия прочности. С этой целью вычисляем фактический момент сопротивления

= =

Находим максимальное нормальное напряжение 10 =10 МПа=[s ].

Условие прочности выполняется, окончательно принимаем d =22, 6см.

Схема б) Исходные данные:

a=2 м; b=3 м; c=1 м; q=15 кН/м;

m=20 кНм; F=30 кН;

[s ] = 160МПа=160 .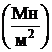

Рис.15 Решение

1.Определение поперечных сил (Q) и изгибающих моментов(M).

Построение их эпюр

а) нахождение опорных реакций

Обозначим опоры буквами A и B соответственно и заменим их действие опорными реакциями (рис.17). Составляем три уравнения

статики (равновесия), используя правило знаков, показанное на рис.16.

Сумма проекций всех сил на горизонтальную ось x

; .

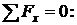
Сумма моментов всех сил относительно точки A

m - q·3(2+1, 5) + R_B·5- F·6 =0;

20- 15·3·3, 5 + R_B·5- 30·6 =0; Рис.16

20- 157, 5 + R_B·5- 180 =0;

-317, 5 + R_B·5=0; R_B= 63,5 кН.

Сумма моментов всех сил относительно точки B

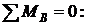- R_A·5+ m + q·3·1, 5- F·1 =0;

- R_A·5 + 20 +15·4, 5 -30 =0;

- R_A·5 + 20 +67, 5 - 30 =0;

-R_A·5 - 57, 5 =0; R_A= 11, 5 кН.