Лекция 11. функции от случайных величин

Очень часто при построении математических моделей рассматриваются случайные величины, связанные функциональной зависимостью.

Например, пусть заданы три случайные величины: Х₁ – количество дефектных компьютеров из общего числа N штук; Х₂ – количество исправных компьютеров из N штук; Х₃ – штраф за поставку некондиционного изделия. Тогда случайные величины Х₂ и Х₃ можно рассматривать как функции от случайной величины Х₁

Х₂ = f₁(Х₁) = N – Х₁, Х₃ = f₂(Х₁) = aХ₁²_.

Другие примеры функций от случайных величин: скорость летательного аппарата – функция от высоты, топлива, аэродинамических свойств, плотности атмосферы и т.д.; уровень благосостояния человека – функция от заработной платы, налогов, стоимости продовольственных и промышленных товаров и услуг и т.д.; количество сердечных сокращений – функция от возраста, высоты местности, температуры тела и т.д.

Пусть в общем случае X – случайная величина, определенная на пространстве элементарных событий W, S – поле событий, Y = f(X), тогда Y = f(Х) – случайная величина, которая каждому w Î W ставит в соответствие число Y(w) = f(X(w)).

По определению случайной величины Y = f(Х) будет случайной величиной только в том случае, если {w| Y(w) < y}ÎS, для любого у. Другими словами, f(Х) – случайная величина, если для любого y определена вероятность события P(Y<y).

Если X – дискретная случайная величина и Y = f(Х) монотонна, то различным значениям Х соответствуют различные значения Y, причем вероятности соответствующих значений Х и Y одинаковы. Другими словами, возможные значения Y находят из равенства

y_i = f(x_i), где x_i возможные значения Х, вероятности возможных значений Y находят из равенства P(Y = y_i) = P(X = x_i). Если же Y = f(Х) немонотонная функция, то различным значениям Х могут соответствовать одинаковые значения Y. В этом случае для отыскания вероятностей возможных значений Y следует сложить вероятности тех значений Х, при которых Y принимает одинаковые значения.

Пример 1. Случайная величина имеет распределение, заданное рядом распределения

xi	– 1
Pi	0,4	0,5	0,1

Найдем ряд распределения случайной величины Y = f(Х) = Х², y₁ =1, y₂ = 1, y₃ = 4, тогда P(Y = 1) = P(Х = х₁) + P(Х = х₂) = 0,4 + 0,5 = 0,9; P(Y = 4) = Р(Х = х₃) = 0,1.

Полученный ряд распределения Y имеет вид

yi
Pi	0,9	0,1

Если Х – непрерывная случайная величина, плотность распределения которой известна, то для того, чтобы найти плотность распределения функции Y = f(Х), надо воспользоваться теоремой.

Теорема 1.ПустьY = f(Х), р(x) – плотность распределения случайной величины Х. Если Y = f(Х) монотонная (т.е. возрастает или убывает), Х – непрерывная случайная величина, то плотность распределения случайной величины Y вычисляется по формуле

. (1)

Доказательство.

1. Пусть Y = f(Х) – монотонно возрастающая функция, тогда существует обратная ей, монотонно возрастающая функция X = f^-1(Y). Из анализа известно, что если f(Х) монотонно возрастающая, то из f(Х) < х Þ X < f^-1(x) (например, f(Х) = 2Х + 3, 2Х + 3 < х Û Х< (х–3)/2 = f^-1(x)). Тогда функция распределения случайной величины Y = f(Х) равна

F_у(x) = P(f(Х) < х) = P(X<f^-1(x)) = F_х (f^-1(x)).

Теперь найдем плотность распределения Y

р_у (x) = (F_у(x))¢ = .(2)

2. Пусть Y = f(Х) – непрерывная монотонно убывающая функция. Тогда и обратная ей функция также монотонно убывающая. Из анализа известно, что если f(Х) монотонно убывающая, то из f(Х)< х Þ X >f^-1(x). Тогда функция распределения случайной величины Y = f(Х) равна

F_у(x) = P(f(Х) < х) = P(X > f^-1(x)) = 1– P(X £ f^-1(x)) =

= 1– P(X < f^-1(x)) – P(X = f^-1(x)) = 1– F_х (f^-1(x).

Найдем плотность распределения Y

р_у (x) = (1 – F_х (f^-1(x)))¢ = – F_х¢ (f^-1(x)) = ,

Так как , то р_у(x) = (3)

Так как в равенстве (2) , то из (2) и (3) следует, что теорема доказана.

Замечание. Если функция Y = f(Х) в интервале возможных значений Х не монотонная, то следует разбить этот интервал на такие интервалы, в которых функция монотонна, и найти плотности распределений для каждого из интервалов монотонности, а затем представить р_у (x) в виде суммы

.

Пример 2. Пусть Y = bX + c, Х – непрерывная случайная величина. Тогда по формуле (1) имеем

. (4)

С помощью формулы (4) можно показать, что если

X ~ N(a,σ), то Y = bX + c ~ N(ab + с, s|b|: (5)

.

Пусть Y = (X–a)/s, X~N(a, s), т.е. в обозначениях формулы (5) b = , c = – , тогда легко посчитать, что Y ~ N(0;1).

При моделировании технико-экономических показателей очень часто используют случайные величины, имеющие логарифмически нормальное распределение.

Определение 1. Неотрицательная случайная величина Y имеет логарифмическое нормальное распределение, если X = lnY имеет нормальное распределение.

Из определения следует, что если Y имеет логнормальное распределение, то оно может быть представлено в виде Y= e^Х, X ~ N(a, s), Х > 0. Найдём плотность распределения р_y(x).

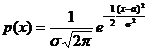, f^-1(x) = lnx, ,

тогда, воспользовавшись формулой (1), получим

(6)

График логнормального распределения в отличие от нормального распределения имеет четко выраженную правостороннюю асимметрию (рис. 1)

0 х

Рис. 1

Пример 3. Найдём функцию и плотность распределения случайной величины, для которой не выполняется условие монотонности.

Пусть Y = X². Если x £ 0, то F_y(x) = Р(Y < x) = 0 и р_y(x) = F_у¢(x) = 0.

Если x>0, то F_y(x) = P(X² < x) = ;

. (7)

Используя данную формулу, найдем плотность распределения квадрата нормальной случайной величины с параметрами а = 0, s = 1.

Пусть Х ~ N(0,1), Y = X², тогда при х > 0

, (8)

а при х £ 0, p_у(х) = 0.

Задача 1. Дискретная случайная величина задана законом распределения

Х	π/4	π/2	3 π/4
Р	0,2	0,7	0,1

Найти закон распределения случайной величины Y = Sin(X).

Задача 2. Случайная величина Х распределена равномерно в интервале (0,π). Найти плотность распределения p_y(x) случайной величины Y = Cos(X).