Действительные функции одной действительной переменной

Действительные функции одной действительной переменной

Способы задания функций:Аналитический, табличный, графический, программный.

Аналитический способ: с помощью формул, частного значения функции, области определения(либо указывается, либо находится).

Неявно заданная функция : F(x,y)=0 . Если уравнение можно разрешить относительно y, то приходим к явно заданной функции. Пример: 3x-y+2=0 y=3x+2

Табличный способ задания функции: x₁,x₂,...,x_n

y₁,y₂,…,y_nПримерытаблицы: ln,sin и т.д.

Также существует графический способ задания функции(наглядный, но неудобный)

Сложная, обратная функция.

Сложная функция –это функция от функции(y=f(g(x)) ).Называетсясуперпозициейфункции. Пример y=sin(x+1).

Обратная функция – функция y=f(x) отображает D(f)->E(f). Также можно говорить об обратной функции x=f^-1(y).Пример y=x³ , x= .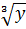

Если числовая функция монотонна, то существует обратная функция x=f^-1(y) Это достаточное условие обратимости.

Основные элементарные функции: 1)Линейная:y=ax+b (a,bϵR) , D(f)=R.

E(f)=Rприa≠0, E(f)={b} приa=0.

2)Квадратичная y=ax²+bx+c , (a,b,c ϵ R; a≠0), D(f)=R.

При а>0 E(f)= 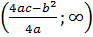, при a<0 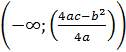график – парабола.

3)Степеннаяy=x^a

4)Показательнаяy=a^x , (a>0; a≠1). D(f)=R , E(f)=(o;∞).

5)Логарифмическаяy=log_ax

6)Тригонометрическая, 7) Обратные тригонометрические,

8)Гиперболические, 9)Обратные гиперболические.

Классификация функций: Целые рациональные, дробно-рациональные, иррациональные, трансцендентные функции sinx, lnxи т.д.

10)Функции заданные параметрическиx=ф(t), где t- параметр, всякую явно заданную функцию можно представить параметрически.

Графики: Окружность(x²+y²=R²) Парабола(y=x²), гипербола(y=x³), астроида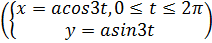

Циклоида(x=a(1-sint), t ϵ R , y=a(1-cost).)

Свойства графиков:

y=-f(x) –зеркально относительно ox

y=f(-x) – зеркально относительно oy

y=f(x-a) – вправо по ox

y=f(x)+b – смещение по oy

y=f(kx) – сжатие по ox

y=Af(x) – растяжение по oy

y=Af(k(x-a))+b – общая формула

Линейная комбинация графиковa₁f₁(x)+a₂f₂(x)

Нелинейнаяf₁(x)*f₂(x)

*******************************************************

Предел функции в заданной точке– такая величина, к которой стремится значение рассматриваемой функции при стремлении её аргумента к данной точке.

Пишут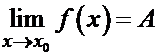

Теорема 1. Если функция f(x) в точке a имеет предел, то этот предел единственный.

Доказательство единственности предела: Допустим противное. Пусть существует такая последовательность x_n 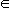, n = 1, 2, ..., что = a и 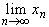= b, причем a 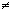b, a,b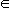 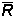. Возьмем какие-либо непересекающиеся окрестности U = U(а) и V = V(b) точек а и b: U V = 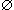. Согласно определению предела вне окрестности U точки а, в частности в окрестности V точки b, содержится лишь конечное число членов последовательности {x_n}. Однако точка b также является ее пределом, и потому в ее окрестности V должны находиться все члены последовательности {x_n}, начиная с некоторого номера, а следовательно, бесконечно много ее членов. Получилось противоречие.

Доказательство ограниченности функции, имеющей конечный предел:

Теорема 1. Если функция f(x) имеет предел в точке a 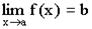,то она ограниченна в некоторой окрестности точки a.

Доказательство:Пусть 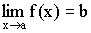, тогда 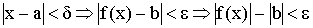, отсюда получаем 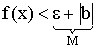. Обратное неверно.

Конкретный пример: 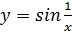в окрестности точки 0.

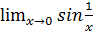– не существует.

Бесконечно малые функции

Функция 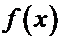называется бесконечно большой при 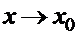, если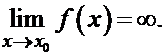

Функция 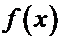называется бесконечно малой при 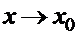, если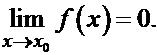

Аналогично определяются бесконечно большие и бесконечно малые функции при .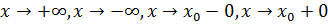

Примеры: f(x)=sinx – бесконечно малая при x->0

f(x)= – бесконечно малая при x->∞, бесконечно большая при x->0.

Теорема 1. Если функция f(x) при x->x₀бесконечно большая, то функция 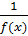при x->x₀ бесконечно малая. Справедливо и обратное утверждение.

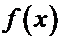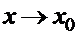Теорема 2. Если функция при имеет конечный предел 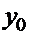, то 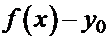бесконечно малая функция при .

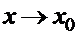Доказательство: 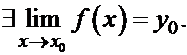Рассмотрим .

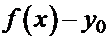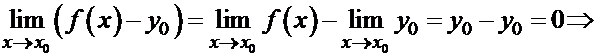
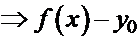- бесконечно малая функция при .

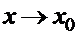Следствие.Если функция 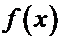при 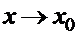имеет конечный предел 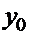, то в окрестности точки 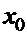она представима в ви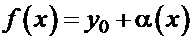де , где 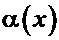- бесконечно малая функция при .

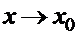Основные свойства бесконечно малых функций:

1. Сумма конечного числа б.м функций является функцией б.м.

2. Произведение б.м функции на ограниченную есть функция б.м.

3. Произведение двух б.м функций есть функция б.м.

4. Произведение б.м функции на константу является б.м функцией.

Первый замечательный предел

Используется для раскрытия неопределённости .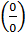

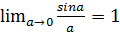–первый замечательный предел.

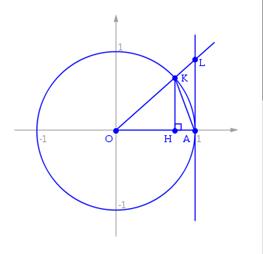- Чертёж для док-ва

Доказательство первого замечательного предела:

Виды неопределённостей: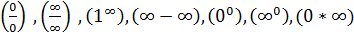

Где 0 – бесконечно малая величина, а ∞ - бесконечно большая величина, по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.

Для раскрытия неопределённостей используются различные методы преобразований, замечательные пределы(первый и второй).

Предел сложной функции.

Теорема 1. Если функцияy=f(x) имеет в точке aконечный пределb и не принимает значения b в некоторой проколотой окрестности U∘(a) этой точки, а функция g(y) имеет в точке b конечный предел c, то сложная функция g(f(x)) имеет предел в точке a, равный c.

Эту теорему нетрудно распространить на суперпозицию более двух функций. Она позволяет использовать замену переменных при вычислении пределов сложных функций по формуле:

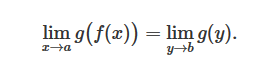
При этом говорят, что под знаком предела в левой части сделана замена f(x)=y. Данная теорема и возможность замены переменных остаются в силе, если хотя бы одна из точек a,b,c будет соответствовать одной из бесконечных точек +∞ или −∞ (или их объединению ∞) на расширенной числовой прямой.

Непрерывность функции

Определение. Функция 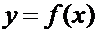называется непрерывной в 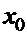, если выполнены три условия:

1) функция 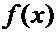определена в точке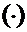 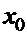, т.е. ;

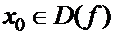2) 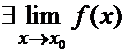3)

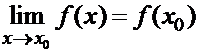
Если нарушается хотя бы одно из условий, то 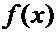разрывна в 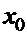,а точка 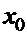- точка разрыва.

Действительные функции одной действительной переменной

Способы задания функций:Аналитический, табличный, графический, программный.

Аналитический способ: с помощью формул, частного значения функции, области определения(либо указывается, либо находится).

Неявно заданная функция : F(x,y)=0 . Если уравнение можно разрешить относительно y, то приходим к явно заданной функции. Пример: 3x-y+2=0 y=3x+2

Табличный способ задания функции: x₁,x₂,...,x_n

y₁,y₂,…,y_nПримерытаблицы: ln,sin и т.д.

Также существует графический способ задания функции(наглядный, но неудобный)

Сложная, обратная функция.

Сложная функция –это функция от функции(y=f(g(x)) ).Называетсясуперпозициейфункции. Пример y=sin(x+1).

Обратная функция – функция y=f(x) отображает D(f)->E(f). Также можно говорить об обратной функции x=f^-1(y).Пример y=x³ , x= .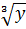

Если числовая функция монотонна, то существует обратная функция x=f^-1(y) Это достаточное условие обратимости.

Основные элементарные функции: 1)Линейная:y=ax+b (a,bϵR) , D(f)=R.

E(f)=Rприa≠0, E(f)={b} приa=0.

2)Квадратичная y=ax²+bx+c , (a,b,c ϵ R; a≠0), D(f)=R.

При а>0 E(f)= 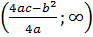, при a<0 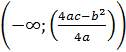график – парабола.

3)Степеннаяy=x^a

4)Показательнаяy=a^x , (a>0; a≠1). D(f)=R , E(f)=(o;∞).

5)Логарифмическаяy=log_ax

6)Тригонометрическая, 7) Обратные тригонометрические,

8)Гиперболические, 9)Обратные гиперболические.

Классификация функций: Целые рациональные, дробно-рациональные, иррациональные, трансцендентные функции sinx, lnxи т.д.

10)Функции заданные параметрическиx=ф(t), где t- параметр, всякую явно заданную функцию можно представить параметрически.

Графики: Окружность(x²+y²=R²) Парабола(y=x²), гипербола(y=x³), астроида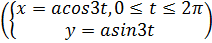

Циклоида(x=a(1-sint), t ϵ R , y=a(1-cost).)

Свойства графиков:

y=-f(x) –зеркально относительно ox

y=f(-x) – зеркально относительно oy

y=f(x-a) – вправо по ox

y=f(x)+b – смещение по oy

y=f(kx) – сжатие по ox

y=Af(x) – растяжение по oy

y=Af(k(x-a))+b – общая формула

Линейная комбинация графиковa₁f₁(x)+a₂f₂(x)

Нелинейнаяf₁(x)*f₂(x)

*******************************************************

Предел функции в заданной точке– такая величина, к которой стремится значение рассматриваемой функции при стремлении её аргумента к данной точке.

Пишут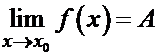

Теорема 1. Если функция f(x) в точке a имеет предел, то этот предел единственный.

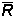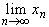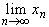Доказательство единственности предела: Допустим противное. Пусть существует такая последовательность x_n , n = 1, 2, ..., что = a и = b, причем a 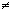b, a,b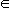 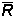. Возьмем какие-либо непересекающиеся окрестности U = U(а) и V = V(b) точек а и b: U V = 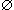. Согласно определению предела вне окрестности U точки а, в частности в окрестности V точки b, содержится лишь конечное число членов последовательности {x_n}. Однако точка b также является ее пределом, и потому в ее окрестности V должны находиться все члены последовательности {x_n}, начиная с некоторого номера, а следовательно, бесконечно много ее членов. Получилось противоречие.

Доказательство ограниченности функции, имеющей конечный предел:

Теорема 1. Если функция f(x) имеет предел в точке a 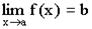,то она ограниченна в некоторой окрестности точки a.

Доказательство:Пусть 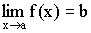, тогда 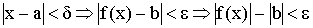, отсюда получаем 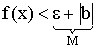. Обратное неверно.

Конкретный пример: 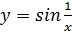в окрестности точки 0.

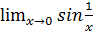– не существует.