Гармонический анализ функции

Задание

1. Функцию f(x), заданную графически на промежутке (0,l), описать аналитически, а для функции f(x), заданной аналитически на промежутке (0,l), построить график.

2. Продолжить функцию f(x) произвольным, четным и нечетным образом на промежутке (-l,0) и построить графики периодически продолженных функций.

3. Проверить достаточные условия разложения периодически продолженных функций в тригонометрический ряд Фурье.

4. Найти коэффициенты Фурье и представить периодически продолженные функции рядом Фурье соответственно общего вида, по косинусам и по синусам.

5. Определить значение разложения функции в точках разрыва и на концах периодов.

6. Представить в аналитическом виде разложение функции в ряд Фурье для всех трех случаев продолжения.

7. Для всех трех случаев разложения функции построить графики сумм

0-й и 1-й гармоник

0-й , 1-й и 2-й гармоник,

0-й , 1-й, 2-й и 3-й гармоник,

любого (большого) числа гармоник (если есть возможность) ряда Фурье, которые совместить с графиками периодически продолженных функций.

8. Вычислить средние квадратические ошибки представления периодически продолженных функций рядом Фурье общего вида, по косинусам и по синусам.

9. Для всех трех случаев разложения функции в ряд Фурье определить амплитудные частотные спектры и построить их графики.

Введение

В математике и физике еще в работах Л. Эйлера и Ж.Л. Лагранжа в 18 веке широкое распространение получил метод разложения периодических функций в ряды по синусам и косинусам, названные тригонометрическими рядами. В 19 веке французский математик и физик Ж. Фурье впервые сформулировал основные требования к функциям, представляемым такими рядами, обеспечивающими их сходимость, заложив основы гармонического анализа. В дальнейшем теория гармонического анализа была развита в работах Дирихле, Гаусса, Римана, Чебышева, Винера, Пэли и других. В частности, гармонический анализ периодических функций был распространен на функции с бесконечным периодом, получивший название интеграла Фурье.

Впоследствии теория преобразования Фурье периодических и непериодических функций вышла далеко за пределы математических дисциплин, став мощной теоретической базой в ряде прикладных областей, таких как радиоэлектроника и радиотехника, теория систем, теория автоматического регулирования, теория сигналов и др.

I. Теоретическая часть

Гармонический анализ

Наиболее распространённым и важным для приложений примером периодических функций являются так называемые гармоники. Это функции вида

y = Asin(ωt +φ),

описывающие незатухающие гармонические колебания с амплитудой A, частотой ω и начальной фазой φ. Они могут быть также записаны в виде

y = asinωt + bcosωt.

Очевидно, период этих функций равен Гармонический анализ функции - student2.ru . Легко убедиться в том, что при сложении гармоник разной частоты график результирующей функции будет заметно отличаться по виду от графика каждой из составляющих.

На практике большое значение имеет задача: можно ли и при каких условиях разложить произвольную периодическую функцию f(x) с периодом T = 2π на сумму простых гармоник разной частоты, то есть представить её в виде суммы гармонических колебаний. Эта задача и составляет гармонический анализ.

Четные и нечетные функции

Функция y=f(x) называется четной, если она не изменяет своего значения при изменении знака аргумента, то есть f(-x)=f(x).

Функция y=f(x) называется нечетной, если при изменении знака аргумента знак функции меняется на противоположный, а её числовое значение сохраняется, то есть f(-x)=-f(x).

II. Практическая часть

Вывод

Таким образом, разложение в ряд Фурье упрощает вычисление значения функции, а в некоторых случаях, это единственный способ решения.

Исходя из выполненной нами курсовой работы, видно, что при увеличении количества сумм гармоник, ряд Фурье все больше, и больше приближается к исходной функции, а в точках разрыва первого рода значение функции численно равно среднему арифметическому между левым и правым пределом.

Погрешности вычислений в каждом из способов разложения функции в ряд Фурье указывают на то, что наиболее точный график получается при разложении по косинусам, так как Гармонический анализ функции - student2.ru 0.0363972441, 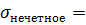0.0914397582, 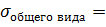0.0286996531.