Осесимметричные задачи теории упругости

Рис.11.1 Рис.11.2

Они возникают при расчете тел вращения. Для упрощения задачи переходят к полярной системе координат. Как видно из рисунка:

Тогда производные вычисляются следующим образом:

.

Далее:

.

Следовательно,

.

Подставляя вместо производных по х, у производные по r, j, с помощью этого соотношения получим новые системы уравнений в полярной системе координат. В случае осесимметричных задач состояние тела не зависит от угла j. То есть производные по , поэтому все уравнения сильно упрощаются.

Примечание. В системе координат х, у была введена функция Эри, через которую вычисляются напряжения:

.

Аналогичную функцию можно ввести в полярной системе координат:

.

Рис.11.3

При этом уравнения равновесия внутреннего элемента будут удовлетворяться автоматически, остается удовлетворить уравнения равновесия граничных элементов и условие совместности деформаций. Последнее принимает вид:

, где .

Общее решение этого уравнения можно найти в справочниках по дифференциальным уравнениям. Оно имеет довольно простой вид:

.

Задача о трубе

Самую большую трудность в теории упругости всегда составляет удовлетворение уравнений равновесия элементов на границе и условий закрепления, но для ряда задач удается получить точное решение.

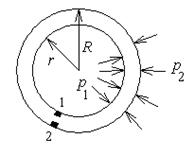
Рис.11.4

В этой задаче решение имеет вид:

.

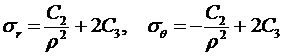С_i – константы интегрирования уравнения. Их находят из условий равновесия граничных элементов 1 и 2. Выражения для них имеют вид:

.

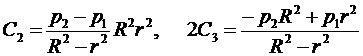Здесь r и R - внутренний и внешний радиусы трубы. Рассмотрим, например, случай отсутствия внутреннего давления. Тогда

.

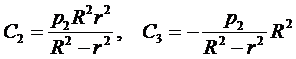Так как R > r, то C₃<0, а также ½С₂/p½<½C₃½, то видно, что s_r уменьшается к центру, s , наоборот, увеличивается к центру. Эпюры напряжений приведены на рис. 11.5. Чтобы проверить на прочность надо проанализировать условие:

.

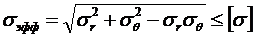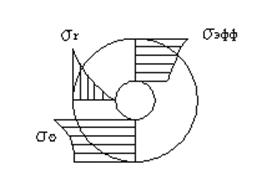
Рис.11.5

Форма кривой s_эфф сильно зависит от отношения .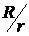

Задача Кирша

Это задача о растяжении бесконечной пластины с круглым отверстием.

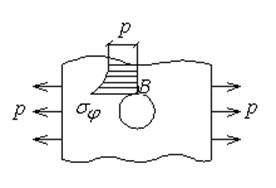
Рис.12.1

Оказывается, что система уравнений в полярной системе координат позволяет решить и кососимметричные задачи. Одной из них является задача о растяжении пластины с отверстием (пластина считается бесконечной). Задача Кирша знаменита тем, что позволяет найти (s_j)_max. Оказывается, что (s_j)_max = 3р. Независимо от размеров и от упругих характеристик материала оно возникает в точке В.

Задачи подобного типа для разных видов отверстий называются задачами о концентрации напряжений.

Следствие: при расчете даже простых тел (типа стержней при растяжении), но с круговыми отверстиями (даже для малого размера отверстия) мы должны увеличивать в 3 раза напряжение, вычисляемое по формуле .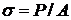

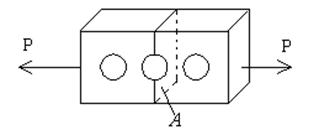
Рис.12.2

Задачи термоупругости

Запишем закон Дюгамеля-Неймана (закон линейного температурного расширения), который гласит, что при изменении температуры тела на величину 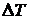оно изменяет свои линейные размеры. Температурная линейная деформация при этом прямо пропорциональна перепаду температуры:

.

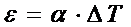Тогда обобщенный закон Гука с учетом закона Дюгамеля- Неймана примет вид:

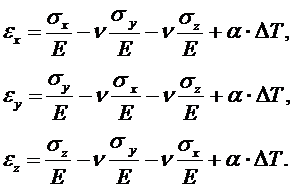
Для изотропного тела изменение температуры не приводит к сдвигам, поэтому:

.

Так как a·DТ=const , то в уравнениях равновесия внутренних элементов a·DТ не участвует, поскольку производные от константы равны нулю, т.е. (a·DТ)′_х=0, (a·DТ)′_у=0. Слагаемое a·DТ входит только в уравнения равновесия граничных элементов и условия закрепления, если их выражаем через деформации.

Приведем точное решение, полученное для задачи о трубе при наличии перепада температур DТ = Т_наружн – Т_внутр. . Оно имеет вид:

Примечание: некоторые конструкции получают температурные напряжения с большими перепадами (от сжимающих до растягивающих). Особенно большие перепады появляются в тех случаях, когда учитываются процессы теплопроводности, то есть процесс перетекания тепла из одной точки в другую. Уравнение, описывающее этот процесс, для плоской задачи имеет вид:

Здесь l - коэффициент, отражающий способность к переносу тепла. F -внутренний источник тепла. Это уравнение практически не имеет точных решений, поэтому такие задачи могут быть решены только приближённо.

ТеориЯ изгиба жестких плит

Основные соотношения этой теории с 3-й попытки получены Софи Жермен в 1816 г. Первая попытка была сделана ею в 1811 г. (инициировал исследования Б. Наполеон, объявив конкурс научных работ по этой теме).

Плита называется жесткой, если ее прогибы малы по сравнению с толщиной. Если прогибы велики, то при жестком закреплении кромок появляются силы растяжения плиты, так как размеры плиты в плане (т.е. по длине и по ширине) не могут увеличиваться.

Гипотезы Кирхгоффа-Лява

Решение ищется в перемещениях:

(14.1)

Рис. 14.1

Из анализа картины деформаций элемента плиты на рис. 14.2 можно заключить, что точки срединной поверхности в плоскости пластины не перемещаются (срединная поверхность - это плоскость, которая равноудалена от верхней и нижней граней, а её уравнение имеет вид z = 0). Тогда перемещения можно разложить в ряд Маклорена в виде:

Так как толщина плиты мала, то величина z тоже мала, поэтому можно принять:

Последнее выражение означает, что толщина пластины принимается неизменной.

Для дальнейшего упрощения функции u_x1, u_y1 выражают через u_z0 из геометрических соображений.

Поскольку толщина пластины не изменяется, то из рис.14.2 видно, что

. (14.2)

Рис. 14.2

Далее из рисунка видно, что a = b, так как это углы с перпендикулярными сторонами (это будет справедливо, если нормаль к срединной плоскости останется нормалью к срединной изогнутой поверхности, нарисованной пунктиром на рис.14.2). Тогда .

Но так как , то

.

А поскольку , то получаем:

.

Согласно (14.2) окончательно получим:

.

Аналогично

.

Для простоты записи функцию u_z = u_zo(x,y) обозначают через w(x,y), которую называют прогибом. Тогда:

(14.3)

Таким образом, перемещения любой точки пластины нам будут известны, если будет известен прогиб w.

Эти упрощенные соотношения (14.3) называются геометрическими соотношениями Кирхгоффа-Лява (1850). Утверждение о том, что нормаль остается нормалью и после деформации, а также утверждение о том, что она не меняет своей длины (т.е. толщина пластины не изменяется) называют геометрическими гипотезами Кирхгоффа-Лява.

Теперь можно вычислить деформации по соотношениям Коши, а затем напряжения по соотношениям закона Гука:

(14.4)

Остальные деформации получаются равными нулю:

(14.5)

Эти соотношения приближенные, так как мы оборвали ряд Маклорена. На самом деле деформации существуют, хотя и малы, а имеет порядок

14.2. Уравнение Софии-Жермен (уравнение для прогиба)

Выпишем уравнения равновесия:

(14.6)

Используем далее закон Гука:

(14.7)

Многочисленными исследованиями было доказано (см., в частности, формулы (14.10), (14.17), (14.19)), что для тонких пластин

. (14.8)

Аналогично

.

Эти соотношения называются статическими гипотезами Кирхгофа-Лява.

Пользуясь соотношением (14.8), из закона Гука (14.7) получим:

Отсюда можно найти σ_х, σ_у:

. (14.9)

Но в уравнениях равновесия σ_z,t_yz,t_xz отбрасывать нельзя. Поскольку производная - это тангенс угла наклона кривой, то даже при малости функций t_yz,t_xz угол их наклона может оказаться очень большим (рис.14.3).

x, z

Рис.14.3

Выразим , e_х и e_у через w по соотношениям Коши:

.

По закону Гука , а напряжения выражаются через деформации по формулам (14.9), следовательно:

(14.10)

Для изотропного материала , тогда

.

Подставим это в первые два уравнения равновесия (14.6).

Тогда из (14.6) получим:

(14.11)

Здесь введено обозначение:

.

Из (14.11) можно найти t_xz, t_yz:

(14.12)

Для отыскания j₁, j₂ используем уравнения равновесия граничных элементов.

Для простоты рассмотрим случай, когда имеется лишь нормальное давление р(х,у) (рис.14.4). Тогда получим, что для элементов, примыкающих к верхней плоскости, т.е. при z= , должны иметь место соотношения статики:

. (14.13)

. (14.14)

При рассмотрении элементов, примыкающих к нижней грани, получим:

. (14.15)

. (14.16)

Рис.14.4

Подставим (14.12) в уравнения (14.13) и получим:

Таким образом, для получаем следующие выражения:

, . (14.17)

Это аналоги известной в сопротивлении материалов формулы Журавского.

Проверим, выполняются ли уравнения равновесия (14.15) для граничных элементов, которые примыкают к нижней грани. Поскольку для них , , то два уравнения равновесия (14.15) тоже выполняются.

Рассмотрим третье уравнение равновесия внутреннего элемента:

.

Подставим сюда выражения для t_xz, t_yz в (14.17). Тогда получим:

. (14.18)

Обозначим:

.

Найдем σ_z, проинтегрировав уравнение (14.18) по z:

_. (14.19)

Функцию ψ(х,у) определяем из уравнения равновесия граничного элемента, примыкающего к нижней грани, т.е. при :

: .

Подставляя , получим:

(14.20)

Введем обозначение:

.

D – называютцилиндрической жесткостью пластины.

Окончательно уравнение для w получим из уравнения равновесия граничного элемента, примыкающего к верхней грани. При должно иметь вид:

при .

Подставляя сюда по формуле (14.19) с учетом (14.20), получим:

. (14.21)

Можно проверить, что уравнение (14.16) будет выполняться тождественно.

Уравнение (14.21) и есть уравнение Софи-Жермен.

Отметим достоинстваполученной теории пластин:

1. Нужно находить только одну функцию w, через нее вычисляются все деформации и напряжения.

2. Функция w имеет физический смысл – это прогиб пластины, поэтому можно решение отыскивать даже по экспериментальным данным.

Отметим некоторые противоречия полученной теории (которые можно условно назвать ее недостатками), которые по сути являются следствиями того, что в разложениях перемещений в ряд Маклорена удержано всего по одному члену.

1. При выводе теории изгиба пластин используется утверждение о том, что нормаль остается нормалью и после деформации, а также утверждение о том, что она не меняет своей длины. Часто они записываются следующим образом: поперечных деформаций нет, т.е. . Отсюда следует, что

.

Это предположение является противоречивым, так как при продольном растяжении-сжатии элемента тела появляются поперечные деформации в виду эффекта Пуассона (рис.14.5). Действительно, согласно закону Гука:

.

Можно видеть (рис.14.5), что соотношение является справедливым только интегрально, т.е. для толщины пластины в целом, т.к. нижняя часть становится тоньше, а верхняя утолщается на такую же величину.

Рис.14.5

Это противоречие не влияет на расчеты на прочность, т.к. деформации не входят в условия прочности.

2. У гипотез Кирхгофа-Лява имеется и второе противоречие. Согласно соотношениям Коши было получено (см. выражения (14.5)), что Тогда из закона Гука для следует, что

= G , = G .

С другой стороны, при выводе уравнения Софи-Жермен (см. аналоги формулы Журавского (14.17)) считалось, что .

Эти противоречия также есть следствие приближенности выражений для перемещений (оборван ряд Маклорена). Как показали теоретические исследования, в тонких пластинах напряжения в сотни и более раз меньше, чем 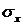, . Это видно и из сравнения соотношений (14.10), (14.17), (14.19). Поэтому по отношению к можно записать:

.

Ясно, что их значения не отражаются на расчетах на прочность изотропных материалов.

3. При подсчете реактивных сил шарнирно опертой пластины в углах расчеты дают сосредоточенные силы, а это противоречит основам теории упругости, так как сосредоточенных сил в природе не существует. Значит, теория Кирхгофа-Лява позволяет получать хорошие решения только внутри области пластины, вблизи края решение может сильно отличаться от истинного, поэтому использование решения задачи о пластине в рамках гипотез Кирхгофа-Лява не допустимо для расчета воздействия на опоры пластины.

4. Возникают трудности при формулировке уравнений равновесия граничных элементов, примыкающих к незакрепленным торцам пластины.