Предмет изучения теории вероятностей

Основные понятия теории вероятностей

Предмет изучения теории вероятностей

Течение окружающей нас действительности и нашей собственной жизни можно представить следующим образом: имеется некоторый набор условий, реализация которых (опыт) приводит всякий раз к несколько различным результатам. Например, взяли монетку в руку, подбросили и ... то ли решка, то ли орел, то ли ребром. Собрались, пошли в институт, расстояние одно и то же, но время в пути каждый раз немного разное. Земля, вращаясь по орбите вокруг Солнца, заняла определенное положение, наступила весна, которая, тем не менее, всегда неповторима.

Эти и еще множество других явлений называются случайными, т.е. от случая к случаю протекающими несколько по-иному.

Однако и в случайном есть свои закономерности. Например, в 18 веке французский ученый Бюффон 4040 раз подряд подбросил монету, в 2048 случаях выпал герб, американский математик Пирсон в начале нашего века подбросил монету 24000 раз, из которых 12012 раз появился герб. Повторение подобного опыта приводит к тому же результату: при большом числе подбрасываний в половине случаев выпадает цифра, в половине - герб. Время прихода в институт также колеблется вокруг некоторой средней величины. В погоде также есть свои закономерности, которые отличают, скажем, погоду средних широт от экваториальной.

Теорией вероятностей называется раздел математики, изучающий закономерности массовых (т.е. повторяющихся многократно) случайных явлений.

При этом подразумевается, что набор основных условий, определяющих исход опыта, остается постоянным. Например, на результаты артиллерийской стрельбы влияют калибр орудия, масса снаряда, заряд, угол наклона и т. д. Изменение хотя бы одного из этих условий приведет к изменению всей картины результатов попаданий.

Изучение теории вероятностей начинается с определения некоторого основного понятия, такого, как число в алгебре, вектор в векторной алгебре, матрица в линейной алгебре. Таким понятием является случайное событие.

Конкретное осуществление случайного явления, которое в результате опыта может произойти, а может и не произойти, называется случайным событием.

Например, выпадение той или иной цифры при бросании игральной кости - случайное явление. Оно может осуществиться через следующие случайные события: появление на верхней грани единицы, двойки, тройки, четверки, пятерки и шестерки. Обычно говорят, что опыт (бросание кости) может завершиться одним из шести исходов.

Случайные события обозначаются обычно большими латинскими буквами A, B, C и т.д.

Численная мера возможности осуществления случайного события называется его вероятностью и обозначается 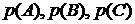и т.д.

Виды случайных событий

Если появление одного из событий исключает наступление другого, они называются несовместными.

Например, выпадение одновременно и цифры и герба при бросании одной монеты.

Если же события могут произойти одновременно, то они называются совместными.

Например, при бросании двух монет могут одновременно выпасть и цифра и герб.

Если вероятности событий одинаковы, то они называются равновозможными.

Например, при бросании точно выполненной однородной игральной кости появление на верхней грани любой цифры равновозможно. Также одинакова вероятность достать любую карту из хорошо протасованной колоды.

Если в результате опыта случайное событие обязательно произойдет, оно называется достоверным.

Например, достоверное событие - замерзание чистой воды при отрицательных температурах.

Невозможным называется событие, которое в результате опыта никогда не наступает.

Например, появление цифры 7 при бросании игрального кубика.

Если несовместные события 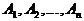таковы, что в результате опыта должно обязательно произойти одно из них, то говорят, что они образуют полную группу.

Например, два стрелка делают по одному выстрелу. Для этого опыта следующие события образуют полную группу:

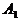- в мишень попали оба;

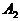- оба промахнулись;

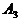- первый попал, второй промахнулся;

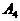- первый промахнулся, второй попал.

Каждое событие из полной для данного опыта группы событий часто называют исходом опыта или элементарным событием.

Если полную группу образуют два события, то они называются противоположными. Событие, противоположное 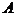, обозначается 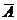. Смысл события, противоположного А, состоит в ненаступлении события А.

Действия с событиями

Если событие 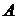состоит в осуществлении хотя бы одного из событий 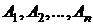, то говорят, что событие 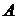равно сумме событий 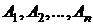и записывают

.

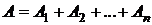Пример . Пусть А - появление четной цифры при бросании кубика , тогда 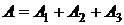, где

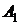- появление двойки;

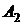- появление четверки;

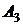- появление шестерки.

Если событие 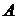состоит в совместном осуществлении событий 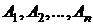, то говорят, что оно равно произведению событий 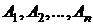и записывают

.

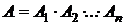Например, если 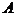- попадание двоих стрелков в мишень при одновременной стрельбе, то 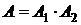, где

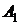- попадание в мишень первого стрелка,

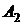- попадание в мишень второго стрелка.

Количественной характеристикой случайного события является его вероятность, способ вычисления которой зависит от того, исходом какого опыта является данное событие. Рассмотрим различные варианты.

Основные понятия теории вероятностей

Предмет изучения теории вероятностей

Течение окружающей нас действительности и нашей собственной жизни можно представить следующим образом: имеется некоторый набор условий, реализация которых (опыт) приводит всякий раз к несколько различным результатам. Например, взяли монетку в руку, подбросили и ... то ли решка, то ли орел, то ли ребром. Собрались, пошли в институт, расстояние одно и то же, но время в пути каждый раз немного разное. Земля, вращаясь по орбите вокруг Солнца, заняла определенное положение, наступила весна, которая, тем не менее, всегда неповторима.

Эти и еще множество других явлений называются случайными, т.е. от случая к случаю протекающими несколько по-иному.

Однако и в случайном есть свои закономерности. Например, в 18 веке французский ученый Бюффон 4040 раз подряд подбросил монету, в 2048 случаях выпал герб, американский математик Пирсон в начале нашего века подбросил монету 24000 раз, из которых 12012 раз появился герб. Повторение подобного опыта приводит к тому же результату: при большом числе подбрасываний в половине случаев выпадает цифра, в половине - герб. Время прихода в институт также колеблется вокруг некоторой средней величины. В погоде также есть свои закономерности, которые отличают, скажем, погоду средних широт от экваториальной.

Теорией вероятностей называется раздел математики, изучающий закономерности массовых (т.е. повторяющихся многократно) случайных явлений.

При этом подразумевается, что набор основных условий, определяющих исход опыта, остается постоянным. Например, на результаты артиллерийской стрельбы влияют калибр орудия, масса снаряда, заряд, угол наклона и т. д. Изменение хотя бы одного из этих условий приведет к изменению всей картины результатов попаданий.

Изучение теории вероятностей начинается с определения некоторого основного понятия, такого, как число в алгебре, вектор в векторной алгебре, матрица в линейной алгебре. Таким понятием является случайное событие.

Конкретное осуществление случайного явления, которое в результате опыта может произойти, а может и не произойти, называется случайным событием.

Например, выпадение той или иной цифры при бросании игральной кости - случайное явление. Оно может осуществиться через следующие случайные события: появление на верхней грани единицы, двойки, тройки, четверки, пятерки и шестерки. Обычно говорят, что опыт (бросание кости) может завершиться одним из шести исходов.

Случайные события обозначаются обычно большими латинскими буквами A, B, C и т.д.

Численная мера возможности осуществления случайного события называется его вероятностью и обозначается 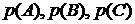и т.д.

Виды случайных событий

Если появление одного из событий исключает наступление другого, они называются несовместными.

Например, выпадение одновременно и цифры и герба при бросании одной монеты.

Если же события могут произойти одновременно, то они называются совместными.

Например, при бросании двух монет могут одновременно выпасть и цифра и герб.

Если вероятности событий одинаковы, то они называются равновозможными.

Например, при бросании точно выполненной однородной игральной кости появление на верхней грани любой цифры равновозможно. Также одинакова вероятность достать любую карту из хорошо протасованной колоды.

Если в результате опыта случайное событие обязательно произойдет, оно называется достоверным.

Например, достоверное событие - замерзание чистой воды при отрицательных температурах.

Невозможным называется событие, которое в результате опыта никогда не наступает.

Например, появление цифры 7 при бросании игрального кубика.

Если несовместные события 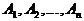таковы, что в результате опыта должно обязательно произойти одно из них, то говорят, что они образуют полную группу.

Например, два стрелка делают по одному выстрелу. Для этого опыта следующие события образуют полную группу:

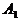- в мишень попали оба;

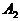- оба промахнулись;

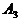- первый попал, второй промахнулся;

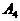- первый промахнулся, второй попал.

Каждое событие из полной для данного опыта группы событий часто называют исходом опыта или элементарным событием.

Если полную группу образуют два события, то они называются противоположными. Событие, противоположное 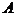, обозначается 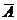. Смысл события, противоположного А, состоит в ненаступлении события А.

Действия с событиями

Если событие 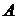состоит в осуществлении хотя бы одного из событий 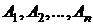, то говорят, что событие 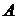равно сумме событий 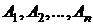и записывают

.

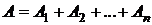Пример . Пусть А - появление четной цифры при бросании кубика , тогда 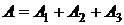, где

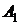- появление двойки;

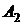- появление четверки;

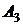- появление шестерки.

Если событие 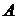состоит в совместном осуществлении событий 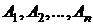, то говорят, что оно равно произведению событий 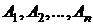и записывают

.

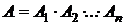Например, если 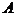- попадание двоих стрелков в мишень при одновременной стрельбе, то 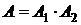, где

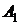- попадание в мишень первого стрелка,

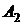- попадание в мишень второго стрелка.

Количественной характеристикой случайного события является его вероятность, способ вычисления которой зависит от того, исходом какого опыта является данное событие. Рассмотрим различные варианты.