Спектральный анализ радиоимпульса

Радиоимпульс – это высокочастотное колебание, огибающая которого имеет форму заданного видеоимпульса. Если s(t) – заданный импульс, то ему соответствует радиоимпульс:

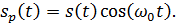(3.1)

Функцию 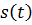называют огибающей радиоимпульса, а функцию 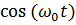– его заполнением, 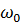- частота заполнения [1].

Спектральная плотность радиосигнала, на основании свойства умножения на косинус, имеет вид:

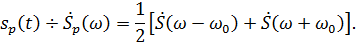
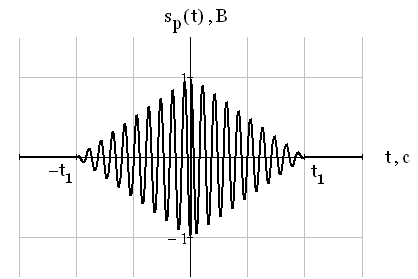
Рис.8 Одиночный радиоимпульс

Значение частоты несущего колебания 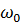выберем из условия: 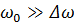, где 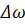-ширина спектра заданного непериодического видеоимпульса, равная 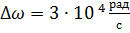. Подберем частоту заполнения 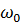, которая должна быть на порядок выше ширины спектра, тогда возьмем .

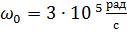Спектр радиоимпульса получается путём переноса спектра его огибающейṠ(ω) из окрестности нулевой частоты в окрестность несущей частоты (±ω₀) с коэффициентом 1/2.

Так как модуль спектральной плотности при (ω >> Δω) стремится к нулю, то спектральные плотности видеоимпульса в положительной и отрицательной области частот практически не влияют друг на друга . И амплитудный спектр радиоимпульса определяется формулой:

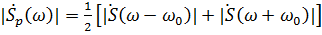(3.2)

Воспользовавшись формулой (3.2) и (1.6) , запишем амплитудный спектр непериодического радиосигнала:

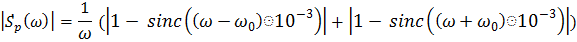
(3.4)

По формуле (3.4) построим амплитудный спектр (рис. 9):

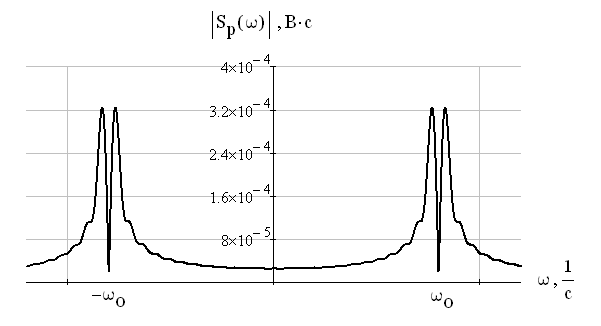
Рис. 9 Амплитудный спектр радиоимпульса

Из графика на рисунке 9 можно сделать вывод, что спектр одиночного радиоимпульса представляет собой сплошной спектр одиночного видеоимпульса, уменьшенный в 2 раза. Спектр радиоимпульса перенесен в область высоких частот на .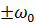

Часть 4

Корреляционный анализ непериодического сигнала

Корреляционный анализ – это анализ сигналов во временной области c целью выявления и оценки их подобия (сходства), основанный на изучении корреляционной функции (КФ) [1].

Корреляционную функцию непериодического сигнала S(t) определяют по формуле [1]:

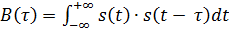(4.1)

Корреляционная функция 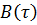характеризует меру сходства сигнала 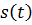с его копией 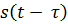, смещенной на интервал ± 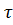[1].

На рисунке 10 изображен сигнал s(t) и его копия, смещённая на τ.

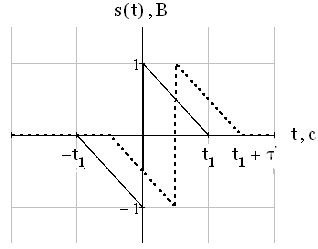
Рис.10. Исходный сигнал и его копия, смещенная на

Найдем корреляционную функцию непериодического сигнала, используя формулу (4.1):

1) При (копия сигнала находится в исходном положении)

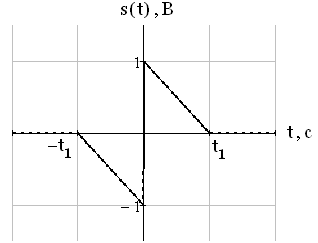
Рис.11. Сигнал и его копия при времени сдвига τ = 0

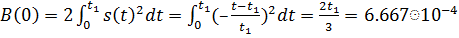(4.2)

2) При 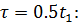(копия сигнала сдвинута вправо на )

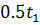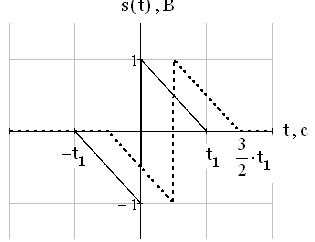
Рис.12. Сигнал и его копия при времени сдвига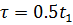

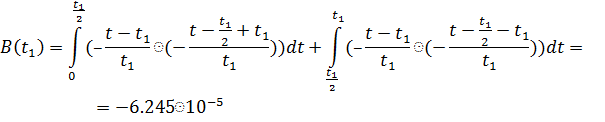
(4.4)

3) При 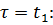(копия сигнала сдвинута вправо на )

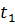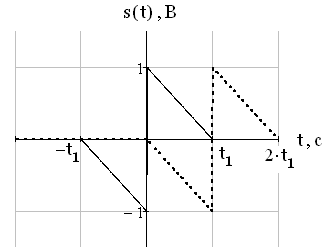
Рис.13. Сигнал и его копия при времени сдвига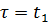

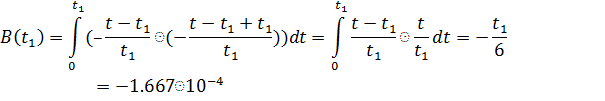
(4.4)

4) При 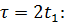(копия сигнала сдвинута вправо на )

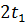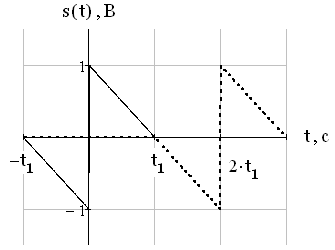
Рис.14. Сигнал и его копия при времени сдвига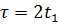

По рис. 14 видно, что сигнал и его копия при 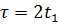не пересекаются. Следовательно, автокорреляционная функция в этом случае будет равна 0.

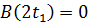(4.5)

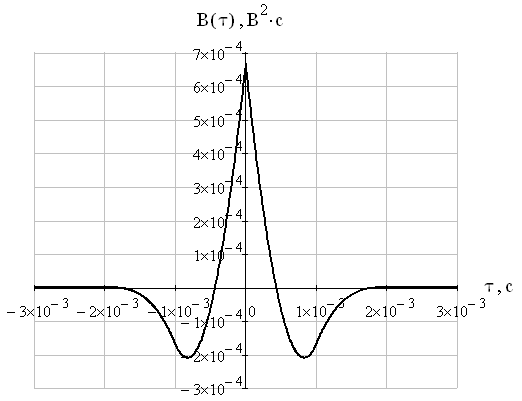
Рис.15. Автокорреляционная функция сигнала S(t)

Из графика на рис.15можно сделать вывод, что корреляционная функция непериодического одиночного видеоимпульса является четной функцией, имеет максимум при τ = 0 и стремится к нулю при τ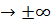

Часть 5