Другие формулировки критерии Поста
I. Система булевых функций полна тогда и только тогда, когда
1) хотя бы одна функция этого множества не сохраняет нуль;
2) хотя бы одна функция этого множества не сохраняет единицу;
3) хотя бы одна функция этого множества несамодвойственная;
4) хотя бы одна функция этого множества нелинейная;
5) хотя бы одна функция этого множества немонотонная.
II. Для того, чтобы система функций была полна, необходимо и достаточно, чтобы в каждом столбце таблицы Поста был хотя бы один минус.
Таблица Поста имеет вид:
| Класс Поста Функция | Т0 | Т1 | L | S | M |
| 1. | |||||
| 2. | |||||
| … |
В результате анализа функций системы в ячейках таблицы проставляются «+» или «-» в зависимости от того, принадлежит ли функция соответствующему классу Поста или не принадлежит.
Если функция не принадлежит ни к одному из классов Поста, то она представляет собой функционально полную систему, т.е. является обобщенной функцией Шеффера.
Входной контроль
1. Запишите определение полной системы булевых функций
2. Сформулируйте критерий Поста.
3. Для чего предназначена таблица Поста?
Ход работы
Задание 1. Для систем булевых функций построены критериальные таблицы Поста. Исследуйте данные системы на функциональную полноту, аргументируя ответ письменно
| а) |  |  |  |  |  | б) | | | | | | |
 | + | - | - | + | - | | + | - | - | + | + | |
 | + | + | - | - | - | | - | + | - | + | - | |
 | - | - | + | - | - |
Задание 2. Исследуйте системы на функциональную полноту:
а) 
;
б) 
;
в) 
Задание 3. Выясните, является ли функция 
обобщенной функцией Шеффера.
Задание 4. Выясните, какая из предложенных булевых функций двух переменных удовлетворяет следующим результатам исследования на принадлежность к классам Поста: 
, 
, 
, 
, 
:
а) 
б) 
в) 
г ) 
Выходной контроль
(выполните самостоятельно по вариантам)
| Задание 1. Исследуйте систему {f(x,y,z), g(x,y,z)} на функциональную полноту: | |
 | |
| Задание 2. Выясните, является ли булева функция обобщенной функцией Шеффера | |
| Вариант 1 | Вариант 2 |
 |  |
Контрольные вопросы
На выполнение тестового контроля отводится 17 минут. Работа состоит из 5 заданий.
К каждому заданию с выбором ответа (1-4) даются 4 варианта ответа, из которых только один правильный. Внимательно прочитайте каждое задание и проанализируйте все варианты предложенных ответов. Верный ответ запишите в отчете по практическому занятию.
В задании на соответствие (5) к каждому элементу первого столбца подберите соответствующий элемент второго. В отчете по практическому занятию запишите в таблицу выбранные буквы под соответствующими цифрами.
Тест выбора
Задание №1.
Вопрос: Основные функционально замкнутые классы булевых функций называются …
Варианты ответа:
а) классами Поста;
б) классами Пифагора;
в) классами Шеффера;
г) классами Буля.
Задание №2.
Вопрос: Система булевых функций 
называется функционально полной, если любую булеву функцию можно представить в виде …
Варианты ответа:
а) композиции некоторого набора булевых функций этой системы;
б) полинома Жегалкина;
в) конъюнктивной нормальной формы;
г) совершенной конъюнктивной нормальной формы.
Задание №3.
Вопрос:Если в каждом столбце критериальной таблицы Поста найдется хотя бы один минус, то система булевых функций…
Варианты ответов:
а) монотонная;
б) линейная;
в) функционально полная;
г) самодвойственная.
Задание №4.
Вопрос:Обобщенной функцией Шеффера называется булева функция n переменных, представляющая собой …
Варианты ответа:
а) систему монотонных функций;
б) функционально полную систему;
в) функционально неполную систему;
г) систему линейных функций.
Тест соответствия
Задание №5.
Вопрос:Установите соответствие между названием класса Поста и общепринятым его обозначением:
Варианты ответа:
| Название класса Поста | Обозначение класса Поста |
| 1) класс линейных функций 2) класс функций, сохраняющих нуль 3) класс функций, сохраняющих единицу 4) класс монотонных функций 5) класс самодвойственных функций | а) Т0 б) Т1 в) М г) Л д) S е) L ж) С |
Ответ:
Условия выполнения:
Задание выполняется письменно в отчете по практическому занятию.
Время на подготовку – 2 мин.
Время на выполнение – 15 мин.
Используются тестовые задания двух типов: тест выбора и тест соответствия.
При выполнении заданий в отчете по практическому занятию рядом с номером выполняемого задания (1-4) записывается номер выбранного ответа.
В задании 5 к каждому элементу первого столбца подбирается соответствующий элемент второго и записываются в таблицу выбранные буквы под соответствующими цифрами.
Критерии оценки:
За каждый правильный ответ выставляется 1 балл.
За не правильный ответ на вопрос выставляется 0 баллов.
Максимальное количество баллов за правильные ответы - 9.
Шкала оценки образовательных достижений:
| Кол-во правильных ответов | Процент результативности (правильных ответов) | Оценка уровня подготовки | |
| балл (отметка) | вербальный аналог | ||
| 90 ÷ 100 | отлично | ||
| 80 ÷ 89 | хорошо | ||
| 70 ÷ 79 | удовлетворительно | ||
| Менее 7 | менее 70 | неудовлетворительно |
Список литературы
Основные источники:
1. Спирина М.С., Спирин П.А. Дискретная математика – М., 2012. – 368 с.
2. 2. Судоплатов С.В., Овчинникова Е.В. Дискретная математика – М.: Инфра-М, 2011. – 256 с.
Дополнительные источники:
1. Галушкина Ю.И., Марьямов А.Н. Конспект лекций по дискретной математике – М., 2008. – 176 с.
2. Канцедал С.А. Дискретная математика – М.: Форум, Инфра-М, 2011. – 224 с.
3. Кочетков П.А. Введение в дискретную математику – М.: МГИУ, 2007. – 88 с.
Практическое занятие № 9
Тема: Определение логического значения для высказываний 
.
Цель: Научиться определять логические значения для высказываний .
Теоретические основы
В математической логике основными понятиями являются два вида предложений: высказывания и высказывательные формы (предикаты).
Высказывательной формой (или предикатом) называется предложение с переменными, которое становится высказыванием, если вместо переменных подставить их значения из некоторого множества.
Примеры:
«x - четное число», «2x-3>0», « 
»
В зависимости от числа переменных различают одноместные, двуместные, ит.д. предикаты.
Обозначения: Р(х), Q (x,y), …
Множество, на котором определен предикат Р(х), называется предметной областью или областью определения предиката, сама переменная х - предметной переменной.
Областью истинности предиката Р(х), заданного на множестве M, называется совокупность всех х из M, при которых данный предикат обращается в истинное высказывание: IP= {x 
М / [P(x)]=И}.
Предикаты, так же, как высказывания, принимают два значения И и Л, поэтому к ним применимы все операции логики высказываний.
Конъюнкцией двух предикатов Р(х) и Q(х) называется новый предикат Р(х)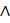 
Q(х), который принимает значение «истина» при тех и только тех значениях 
, при которых каждый из предикатов Р(х) и Q(х) принимает значение «истина».
Очевидно, что областью истинности предиката Р(х) 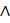Q(х) является общая часть областей истинности предикатов Р(х) и Q(х), т.е. пересечение 
.
Дизъюнкцией двух предикатов Р(х) и Q(х) называется новый предикат 
, который принимает значение «ложь» при тех и только тех значениях , при которых каждый из предикатов принимает значение «ложь».
Областью истинности предиката 
является объединение областей истинности предикатов Р(х) и Q(х), то есть объединение 
.
Отрицанием предиката Р(х) называется новый предикат 
, который принимает значение «истина» при всех значениях 
, при которых предикат Р(х) принимает значение «ложь».
Областью истинности предиката является дополнение области истинности предиката Р(х), т.е. 
Импликацией предикатов Р(х) и Q(х) называется новый предикат 
, который является ложным при тех и только тех значениях , при которых одновременно Р(х) принимает значение «истина», а Q(х) – значение «ложь.
Областью истинности предиката является объединение дополнения области истинности предиката Р(х) и области истинности предиката Q(х), т.е. 
Наряду с образованием из предикатов высказываний путем подстановки конкретного значения предметной переменной, в логике рассматривается еще две операции, которые превращают одноместный предикат в высказывание - употребление квантор всеобщности (общности) (читается «для всех…», «для каждого…») и квантор существования (читается как «существует такой…», «хотя бы для одного…»).
Предикат вместе с квантором становится высказыванием.
Высказывания 
называются общими утверждениями, 
- частными утверждениями.
Часто используют словосочетание «существует единственный…», в логике это записывается с помощью знака 
.
Высказывание считается истинным, если 
истинно при подстановке вместо 
любого элемента из М.
Высказывание 
считается истинным, если истинно при подстановке вместо хотя бы одного элемента из М.
Истинность общих утверждений доказывается в общем виде, частного утверждения – с помощью примера.
Ложность общих утверждений доказывается приведением контрпримера (т.е. путем приведения такого значения переменной x, при котором ложно), частного утверждения – в общем виде.
Переменную х в предикате Р(х) называют свободной (ей можно придавать различные значения из М), в высказывании 
переменную х называют связанной квантором 
.
Для высказывательных форм справедливы все известные законы логики. Кроме того, справедливы и кванторные законы:
1. 
2. 
3. 
4. 
5. Разноименные кванторы менять местами нельзя!!!
Входной контроль
1. Запишите определения понятий: «предикат», «квантор», «частное утверждение», «общее утверждение».
2. Какие логические операции могут быть выполнены над предикатами?
3. Как доказать истинность / ложность общих / частных утверждений?
4. Приведите 1-2 примера общих / частных утверждений из литературных произведений, кинофильмов, песен и т.д.