Определимого стержня при растяжении - сжатии

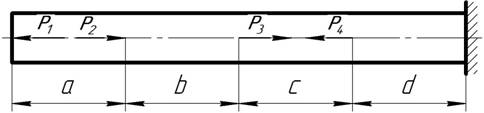
Чугунный стержень, закрепленный с одной стороны, загружен силами P₁ = 40 кН, Р₂ = 70 кН, Р₃ = 30 кН, Р₄ = 110 кН. Продольные размеры стержня: а = 1м, b = 1,2 м, с = 2 м, d = 0,8 м. Допускаемые напряжения на растяжение [s_р] = 50 МПа, допускаемые напряжения на сжатие [s_сж] = 200 МПа. Модуль нормальной упругости Е = 2∙10⁵ МПа.

Требуется определить:

1) Из условия прочности диаметры поперечных сечений на каждом участке стержня;

2) Из условия прочности диаметр круглого, постоянного по всей длине стержня и сравнить массу полученного стержня с массой стержня, полученного в п.1;

3) Деформацию ступенчатого стержня.

4) Деформацию круглого, постоянного по всей длине стержня, и сравнить ее с полученной в п.3.

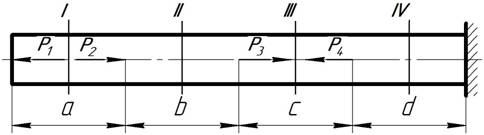
Под действием внешних нагрузок (Р₁, Р₂, Р₃, Р₄)в теле стержня возникают внутренние усилия - напряженияs,величина которых определяется методом сечений. По этому методу в том месте, где определяются напряжения проводится сечение и рассматривается равновесие одной части стержня под действием внешних сил действующих на эту часть и внутренних усилий действующих в сделанном сечении.

Рассмотрим часть стержня левее сечения I-I . На рассматриваемую часть действует внешняя сила Р₁.По сечению I-I действуют внутренние усилия - напряжения s_I,равнодействующая которых - N_I.

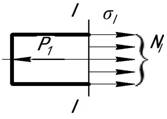
Рассматриваем равновесие этой части стержня:

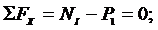
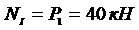
Из условия прочности необходимая величина площади поперечного сечения этой части стержня А_I определится:

.

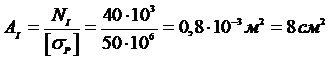Диаметр первой части стержня определится:

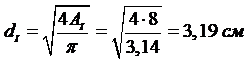
Изменение длины участка «а»:

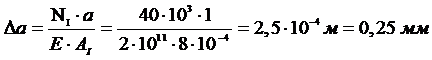
Рассмотрим часть стержня левее сечения II-II. На рассматриваемую часть действуют внешние силы Р₁ и Р₂.

По сечению II-II действуют внутренние усилия-напряжения

Рис.3

s_II , равнодействующая которых - N_II.

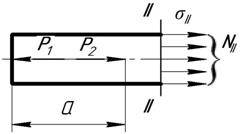
Рассматриваем равновесие этой части стержня:

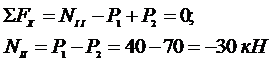
Как видно, в уравнение N внешняя сила входит со знаком плюс если направлена от сечения(Р₁) и со знаком минус, если направлен к сечению (Р₂). Или же растягивающая сила со знаком плюс, сжимающая со знаком минус. И если в результате вычисления получаем N со знаком плюс это значит, что рассматриваемый участок растянут, а если со знаком минус - то сжат. Полученное значение N_II = -30 кН говорит о том, что второй участок сжат и при определении площади сечения необходимо брать допускаемое напряжения для сжатия [s_сж] = 200 МПа.

Необходимая площадь поперечного сечения:

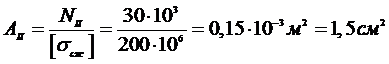
Диаметр второй части стержня:

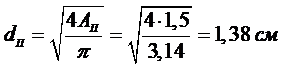
Изменение длины участка «b»:

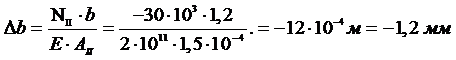
Рассмотрим часть стержня левее сечения III-III. На рассматриваемую часть действуют внешние силы Р₁ ,Р₂ и Р₃.

По сечению III-III действуют внутренние усилия - напряжения s_III, равнодействующая которых - N_III.

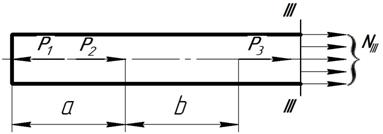
Рассматриваем равновесие этой части стержня:

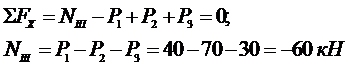
Необходимая площадь поперечного сечения А_III:

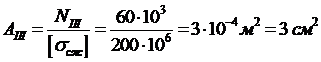
Диаметр третьей части стержня определится:

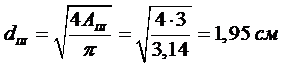
Изменение длины участка «с»:

Рис. 5

Рассмотрим часть стержня левее сечения IV-IV. На рассматриваемую часть действуют внешние силы Р₁, Р₂ Р₃ и P₄.

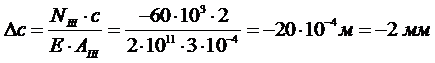
По сечению IV-IV действуют внутренние усилия - напряжения s_IV, равнодействующая которых - N_IV.

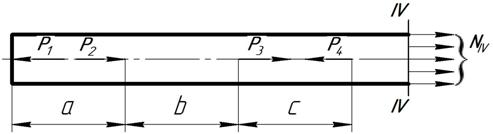
Рассматриваем равновесие этой части стержня:

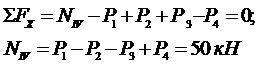
Необходимая площадь поперечного сеченияА_IV :

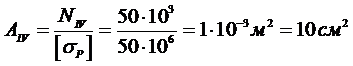
Диаметр четвёртой части стержня определится

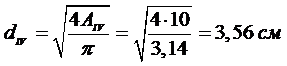
Изменение длины участка «d»:

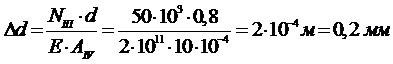
Суммарная деформация всего стержня 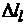складывается из деформаций отдельных его частей:

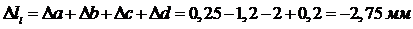
На сновании результатов расчёта делается чертёж стержня. Диаметры частей указаны в сантиметрах. Все части стержня будут загружены на 100%.

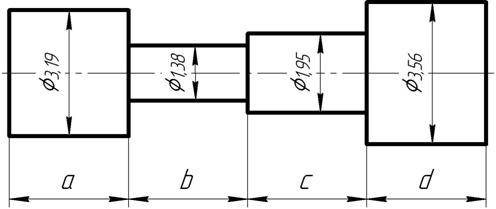
Объём части стержня длиной «a»:

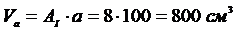
Объём части стержня длиной «b»:

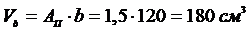
Объём части стержня длиной «c»:

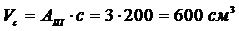
Объём части стержня длиной «d»:

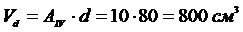
Полный объём всего стержня:

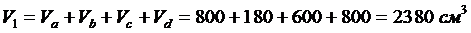
Если стержень изготавливать по всей длине одинакового диаметра, то он будет равен 3,56 см. В этом случае часть «d» будет загружена на 100%, а все остальные будут недогружены.

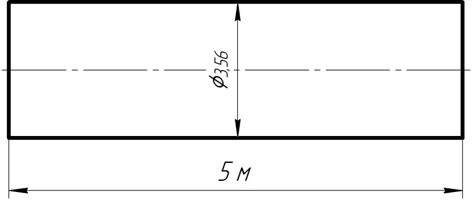
Объем стержня в этом случае будет:

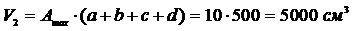
Так как объем и масса прямо пропорциональны через плотность материала, то из соотношения объёмов и следовательно масс, будет:

.

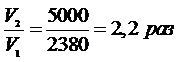Деформация стержня постоянного поперечного сечения по всей длине определится:

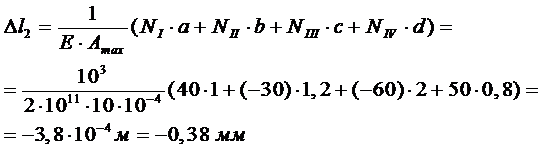
Соотношение деформаций стержней по второму и первому варианту:

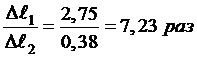
Пример расчета РГР 2

РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМОЙ БАЛКИ

НА ПРОЧНОСТЬ

Для балки, изображённой на рис.1, загруженной сосредоточенными силами Р₁=20кН, Р₂=40кН, равномерно распределённой нагрузкой q=10кН/м и сосредоточенныммоментомМ₀=30кН·мтребуется:

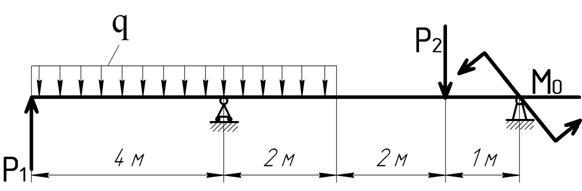
Рис. 1. Схема нагружения балки

1. Начертить ее в масштабе по данным своего шифра;

2. Определить реакции опор;

3. Построить эпюры изгибающих моментов и поперечных сил;

4. Из условия прочности по нормальным напряжениям [s] =160 МПа определить размеры круглого и двутаврового сечений.

5. Сравнить массы полученных балок и выбрать вариант с наименьшей материалоемкостью;

6. Проверить выбранное сечение на касательные напряжения;

Определение реакций опор.

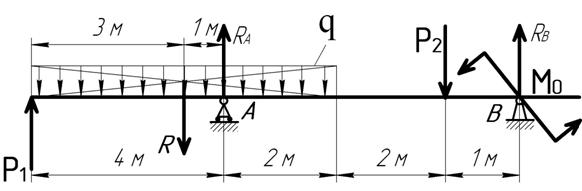
Рис. 2. Схема к определению опорных реакций.

В точках закрепления балки к основанию (точки А и В) прикладываем реакции опор R_A и R_B. Равнодействующая R равномерно распределённой нагрузки q (рис. 2.) определится:

R = q · 6 = 10 · 6 = 60 кН.

Равнодействующая приложена в середине участка: т.е. в трёх метрах от левого края.

Определяем реакции R_А и R_В.

Составляем уравнения статики:

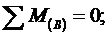
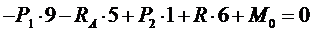
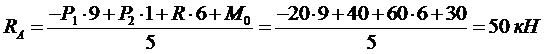
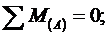
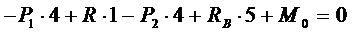
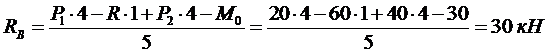
Для проверки записываем уравнение:

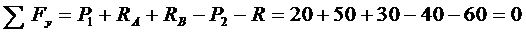
Следовательно, реакции опор R_A и R_B найдены верно.