Доверительные интервалы и области для коэффициентов регрессии
Полученные до настоящего времени оценки  реальных коэффициентов регрессии
реальных коэффициентов регрессии  называют точечными, так как они представляют собой конкретные значения, выраженные на числовой оси как точки. Возникает вопрос, на сколько точечные оценки
называют точечными, так как они представляют собой конкретные значения, выраженные на числовой оси как точки. Возникает вопрос, на сколько точечные оценки  отличаются от истинных оценок
отличаются от истинных оценок  . Отвечая на данный вопрос строятся доверительные интервалы (рис. 10), на которых показаны все возможные значения оценочного коэффициента регрессии
. Отвечая на данный вопрос строятся доверительные интервалы (рис. 10), на которых показаны все возможные значения оценочного коэффициента регрессии  для
для  .
.

Рис. 10. Доверительный интервал коэффициента 
Доверительный интервал случайной величины  - интервал с заданными левой
- интервал с заданными левой  и правой
и правой  границами, в которых с наперед заданной вероятностью
границами, в которых с наперед заданной вероятностью  (доверительная вероятность) заключено истинное значение
(доверительная вероятность) заключено истинное значение  .
.
Вводится соотношение (24), имеющее распределение Стьюдента (t-распределение) с числом степеней свободы соответствующим  .
.
 (24)
(24)
Число степеней свободы определяется по формуле  , где
, где  - диагональный элемент матрицы
- диагональный элемент матрицы  ,
,  - матрица регрессоров (5) (например, для
- матрица регрессоров (5) (например, для  соответствует
соответствует  ).
).
Следовательно, выражение (24) можно представить в виде (25).
 (25)
(25)
Доверительный интервал для i-ого коэффициента  строится по выражению (26).
строится по выражению (26).
 (26)
(26)
где
 - критическое значение, берется из таблицы распределения Стьюдента (табл. 3) с учетом числа степеней свободы
- критическое значение, берется из таблицы распределения Стьюдента (табл. 3) с учетом числа степеней свободы  , соответствующего знаменателю оценки
, соответствующего знаменателю оценки  (если
(если  определялась из
определялась из  дополнительных одинаковых наблюдений, то
дополнительных одинаковых наблюдений, то  ), и уровню значимости
), и уровню значимости 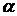 (
(  );
);
 - число дополнительных наблюдений при одинаковых условиях (фиксированных значениях факторов
- число дополнительных наблюдений при одинаковых условиях (фиксированных значениях факторов  );
);
 - оценивается по формуле (17).
- оценивается по формуле (17).
Табл. 3. Критические точки распределения Стьюдента
Число степеней свободы  | Уровень значимости 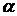 (двухсторонняя критическая область) (двухсторонняя критическая область) | |||||
| 0.10 | 0.05 | 0.02 | 0.01 | 0.002 | 0.001 | |
| 6.31 | 12.7 | 31.82 | 63.7 | 318.3 | 637.0 | |
| 2.92 | 4.30 | 6.97 | 9.92 | 22.33 | 31.6 | |
| 2.35 | 3.18 | 4.54 | 5.84 | 10.22 | 12.9 | |
| 2.13 | 2.78 | 3.75 | 4.60 | 7.17 | 8.61 | |
| 2.01 | 2.57 | 3.37 | 4.03 | 5.89 | 6.86 | |
| 1.94 | 2.45 | 3.14 | 3.71 | 5.21 | 5.96 | |
| 1.89 | 2.36 | 3.00 | 3.50 | 4.79 | 5.40 | |
| 1.86 | 2.31 | 2.90 | 3.36 | 4.50 | 5.04 | |
| 1.83 | 2.26 | 2.82 | 3.25 | 4.30 | 4.78 | |
| 1.81 | 2.23 | 2.76 | 3.17 | 4.14 | 4.59 | |
| 1.80 | 2.20 | 2.72 | 3.11 | 4.03 | 4.44 | |
| 1.78 | 2.18 | 2.68 | 3.05 | 3.93 | 4.32 | |
| 1.77 | 2.16 | 2.65 | 3.01 | 3.85 | 4.22 | |
| 1.76 | 2.14 | 2.62 | 2.98 | 3.79 | 4.14 | |
| 1.75 | 2.13 | 2.60 | 2.95 | 3.73 | 4.07 | |
| 1.75 | 2.12 | 2.58 | 2.92 | 3.69 | 4.01 | |
| 1.74 | 2.11 | 2.57 | 2.90 | 3.65 | 3.95 | |
| 1.73 | 2.10 | 2.55 | 2.88 | 3.61 | 3.92 | |
| 1.73 | 2.09 | 2.54 | 2.86 | 3.58 | 3.88 | |
| 1.73 | 2.09 | 2.53 | 2.85 | 3.55 | 3.85 | |
| 1.72 | 2.08 | 2.52 | 2.83 | 3.53 | 3.82 | |
| 1.72 | 2.07 | 2.51 | 2.82 | 3.51 | 3.79 | |
| 1.71 | 2.07 | 2.50 | 2.81 | 3.59 | 3.77 | |
| 1.71 | 2.06 | 2.49 | 2.80 | 3.47 | 3.74 | |
| 1.71 | 2.06 | 2.49 | 2.79 | 3.45 | 3.72 | |
| 1.71 | 2.06 | 2.48 | 2.78 | 3.44 | 3.71 | |
| 1.71 | 2.05 | 2.47 | 2.77 | 3.42 | 3.69 | |
| 1.70 | 2.05 | 2.46 | 2.76 | 3.40 | 3.66 | |
| 1.70 | 2.05 | 2.46 | 2.76 | 3.40 | 3.66 | |
| 1.70 | 2.04 | 2.46 | 2.75 | 3.39 | 3.65 | |
| 1.68 | 2.02 | 2.42 | 2.70 | 3.31 | 3.55 | |
| 1.67 | 2.00 | 2.39 | 2.66 | 3.23 | 3.46 | |
| 1.66 | 1.98 | 2.36 | 2.62 | 3.17 | 3.37 | |
| ¥ | 1.64 | 1.96 | 2.33 | 2.58 | 3.09 | 3.29 |
| 0.05 | 0.025 | 0.01 | 0.005 | 0.001 | 0.0005 | |
Уровень значимости 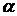 (односторонняя критическая область) (односторонняя критическая область) |
Индивидуальные доверительные интервалы можно строить для любого регрессионного коэффициента  . Причем длина интервала существенно зависит от выбранного значения
. Причем длина интервала существенно зависит от выбранного значения 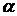 . Чем меньше
. Чем меньше 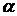 , тем больше доверительный интервал. Слишком большие доверительные интервалы бесполезны, следовательно, нет смысла выбирать слишком малые значения параметра
, тем больше доверительный интервал. Слишком большие доверительные интервалы бесполезны, следовательно, нет смысла выбирать слишком малые значения параметра 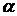 .
.
Доверительные интервалы обладают значительным недостатком, обусловленным невозможностью учета коррелированности оценок регрессионных коэффициентов  , если корреляция оценками
, если корреляция оценками  и
и  присутствует. В подобных случаях строятся доверительные области (27).
присутствует. В подобных случаях строятся доверительные области (27).
 (27)
(27)
где
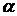 - принятый исследователем уровень значимости;
- принятый исследователем уровень значимости;
 - оценивается по формуле (17);
- оценивается по формуле (17);
 - число степеней свободы оценки
- число степеней свободы оценки  ;
;
 - число регрессоров;
- число регрессоров;
 - матрица регрессоров (5).
- матрица регрессоров (5).
Таким образом, для модели с двумя коэффициентами на основании (27) получается эллиптическая доверительная область (рис. 11), центр которой рассчитывается при помощи МНК.

Рис. 11. Эллиптическая доверительная область
Однако, эллиптические области показывают представление о положении вектора истинного значения для двух регрессоров. Когда же речь идет о большем количестве регрессоров, то подобная форма не годится в силу невозможности визуального представления, а, следовательно, становится затруднительной и оценка истинного положения дел.
При  используют доверительные интервалы Бонферони.
используют доверительные интервалы Бонферони.
Доверительный интервал Бонферрони случайной величины  - интервал с заданными левой
- интервал с заданными левой  и правой
и правой  границами, в которых с наперед заданной вероятностью
границами, в которых с наперед заданной вероятностью  (доверительная вероятность) заключено истинное значение
(доверительная вероятность) заключено истинное значение  , где
, где  - число регрессоров модели. Доверительная вероятность
- число регрессоров модели. Доверительная вероятность  , введенная Бонферрони, играет важную роль при оценке адекватности регрессионных моделей с более чем одним фактором
, введенная Бонферрони, играет важную роль при оценке адекватности регрессионных моделей с более чем одним фактором  . Таким образом, доверительная вероятность
. Таким образом, доверительная вероятность 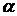 равномерно распределяется между
равномерно распределяется между  регрессорами.
регрессорами.
Доверительный интервал Бонферрони для i-ого коэффициента  строится по выражению (26) с учетом того, что (
строится по выражению (26) с учетом того, что (  ).
).
